p.16 能量(Energy)與功(Work) 在1676-1689之間, Leibniz定義vis viva(拉丁文:living force)=mv2, 同時相信“total vis viva”守恆不嬖變 Willem's Gravesande(1688-1742), 做了一個實驗: 個類似的問題: 一 輛車的速度加倍,它的 荷蘭哲學家及數學家 煞車距離應該增加幾倍? Willem's Gravesande (1688-1742) 黏土中的坑印深度與 V呈何種關係? 黏土 交摄大學李威篱 2013物理興想
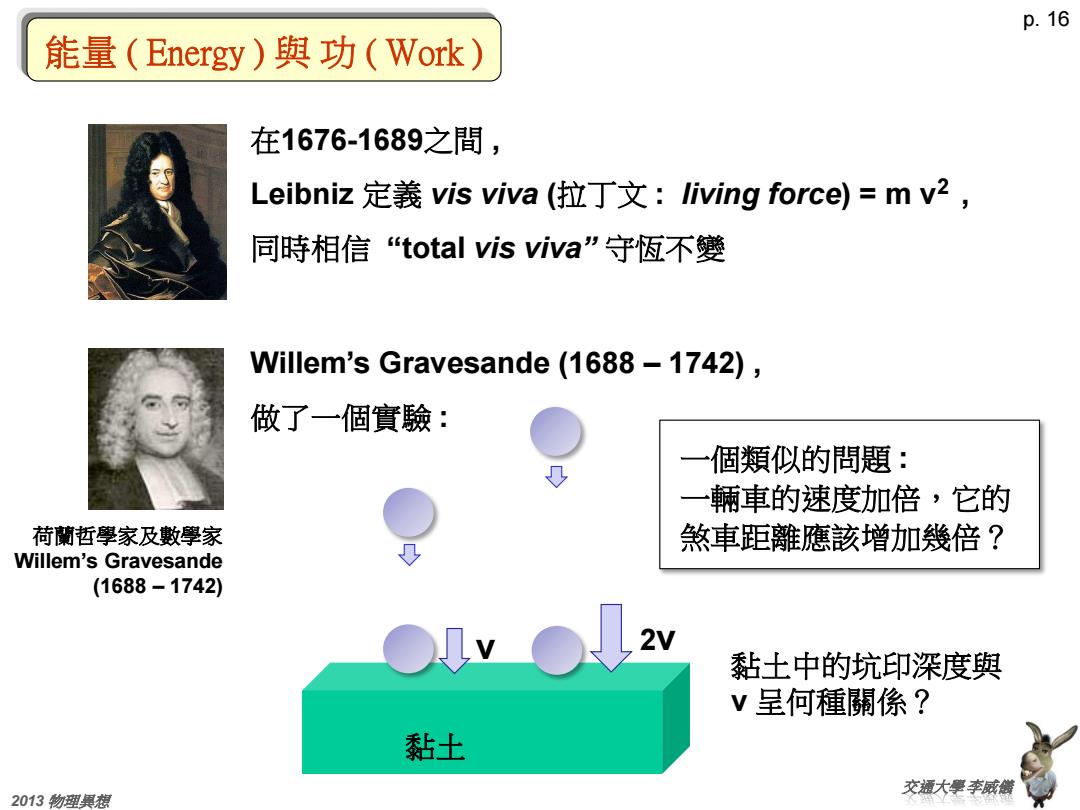
p. 16 交通大學 李威儀 2013 物理異想 能量 ( Energy ) 與 功 ( Work ) 在1676-1689之間 , Leibniz 定義 vis viva (拉丁文 : living force) = m v2 , 同時相信 “total vis viva” 守恆不變 Willem’s Gravesande (1688 – 1742) , 做了一個實驗 : 荷蘭哲學家及數學家 Willem’s Gravesande (1688 – 1742) 黏土 v 黏土中的坑印深度與 v 呈何種關係? 2v 一個類似的問題 : 一輛車的速度加倍,它的 煞車距離應該增加幾倍?

p.17 1740年為13歲的兒子寫了“Institutions de Physique”(英文“Lessons in Physics”)一書,講述科學與哲學方面 的最新思想。書中結合了Leibniz的理論及 Gravesande的實驗,認為運動中物體的 v is viva或“quantity of motion'”等於 mv2。 Emilie du Chatelet 法國物理學家、數學家 1706-1749 1749年完成了牛頓《自然哲學的數學原理》 一書的法文翻譯,Chatelet去世十年後才 出版,至今仍是牛頓《自然哲學的數學原 理》的法文翻譯標準本。 交酒大學李威德 2013物理果想
p. 17 交通大學 李威儀 2013 物理異想 É milie du Châtelet 法國物理學家、數學家 1706 - 1749 1740年為13歲的兒子寫了 “Institutions de Physique” ( 英文 “Lessons in Physics” )一書,講述科學與哲學方面 的最新思想。書中結合了Leibniz的理論及 Gravesande 的實驗,認為運動中物體的 v is viva 或 “quantity of motion” 等於 mv2 。 1749年完成了牛頓《自然哲學的數學原理》 一書的法文翻譯, Châtelet 去世十年後才 出版,至今仍是牛頓《自然哲學的數學原 理》的法文翻譯標準本

p.18 能量(Energy) ·1676-1689 Leibniz定義vis viva(拉丁文:living force)=mv2,同時認為“total vis viva”應該是守恆不變的 ·1802 Thomas Young在對英國皇家學會的演講中第一次使用“energy”的 名稱取代“vis viva”,並在1807年發表的書中宣稱: "The product of the mass of a body into the square of its velocity may properly be termed its energy." ·1829 Gaspard Coriolis定義了動能(kinetic energy) ·1853 William Rankine定義了位能(potential energy) 交酒大學李威德 2013物理興想
p. 18 交通大學 李威儀 2013 物理異想 能量 ( Energy ) • 1676-1689 Leibniz 定義 vis viva (拉丁文 : living force) = m v2 ,同時認為“total vis viva” 應該是守恆不變的 • 1802 Thomas Young 在對英國皇家學會的演講中第一次使用 “energy” 的 名稱取代 “vis viva” , 並在1807年發表的書中宣稱 : “The product of the mass of a body into the square of its velocity may properly be termed its energy.” • 1829 Gaspard Coriolis 定義了動能 (kinetic energy) • 1853 William Rankine 定義了位能 (potential energy)
p.19 常力所作的功(Work Done by a Constant Force) 0 0。▣:0◆ F cose 要有出力才有“功”勞 造成位移才有“功”勞 s W =F cos 0.s Joule,a scalar ◆中 =F·sorF·△X F:force,s:displacement W:work 1J=1N·1m=(kgm2)1s2 W:mechanical work different from chemical work 交酒大學李威德 2013物興想
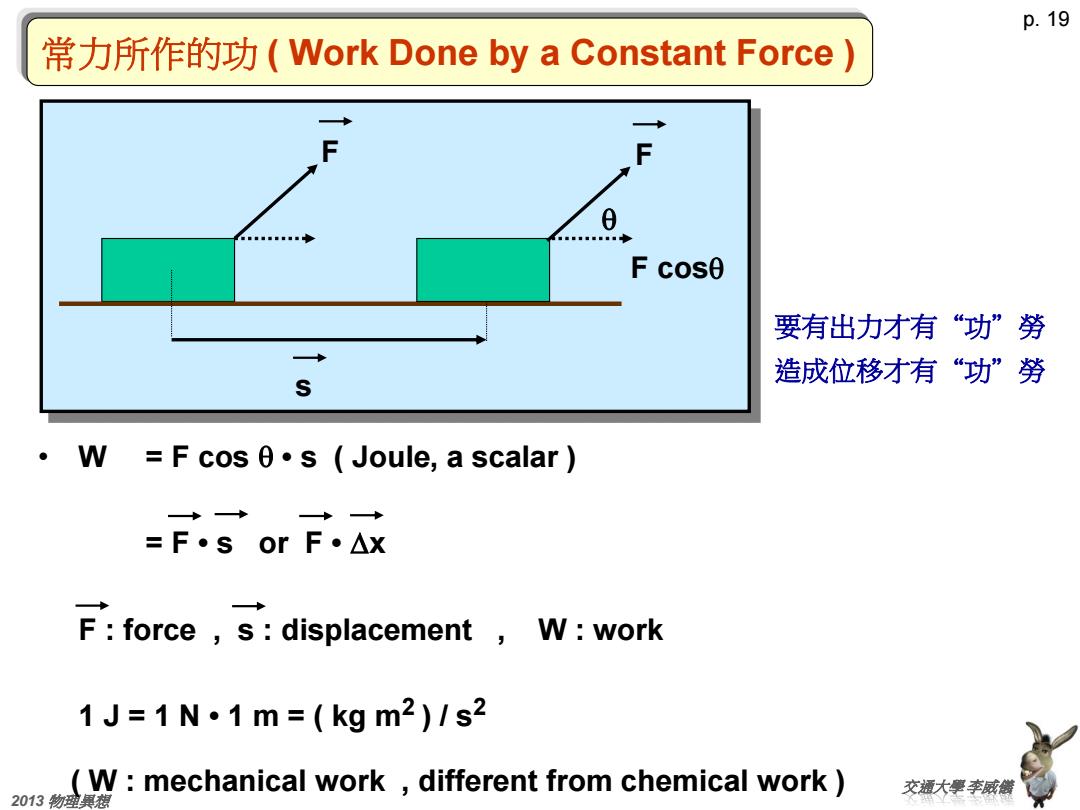
p. 19 交通大學 李威儀 2013 物理異想 • W = F cos q • s ( Joule, a scalar ) = F • s or F • Dx F : force , s : displacement , W : work 1 J = 1 N • 1 m = ( kg m2 ) / s2 ( W : mechanical work , different from chemical work ) F s F F cosq q 要有出力才有“功”勞 造成位移才有“功”勞 常力所作的功 ( Work Done by a Constant Force )

p.20 動能(Kinetic Energy) >cause v change →cause x change W→cause?change in one-dim.,const.force W=Fx△x=ma△x 垂直於運動方向的力沒有作功 v2=v。2+2a△x →不會改變物體的動能 a△x=h(w2-v2) 例如:等速率圓周運動 →W=hmv2-hmv。2 define kinetic energy (K.E.)Ek=%2 mv2 joule,scalar Wnet=△Ek:Work-Energy Theorem(功能定律) Work-Energy Theorem still valid in 3-dim.space and with non-constant forces. 交通大學李威 2013物理果想
p. 20 交通大學 李威儀 2013 物理異想 F cause v change v cause x change W cause ? change in one-dim. , const. force : W = Fx Dx = ma Dx v 2 = vo 2 + 2a Dx a Dx = ½ (v2 – vo 2 ) W = ½ mv2 – ½ mvo 2 define kinetic energy ( K.E. ) : Ek = ½ mv2 ( joule, scalar ) Wnet = DEk : Work – Energy Theorem ( 功能定律 ) ( Work-Energy Theorem still valid in 3-dim. space and with non-constant forces. ) 動能 ( Kinetic Energy ) 垂直於運動方向的力沒有作功 不會改變物體的動能 例如 : 等速率圓周運動