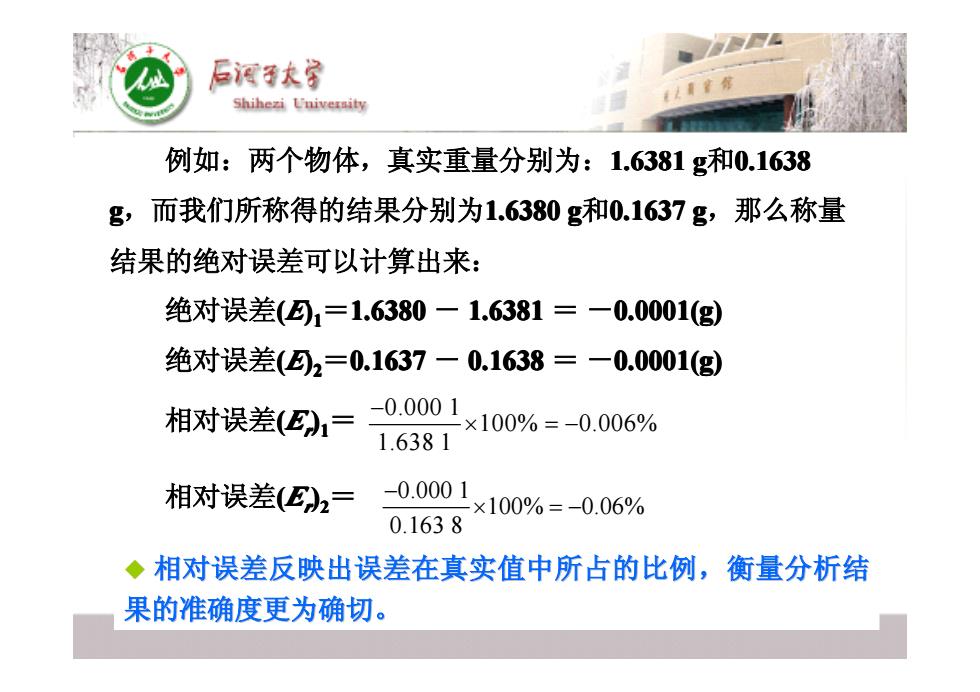
E酒3大学 Shihezi University 例如:两个物体,真实重量分别为:1.6381g和0.1638 g,1 而我们所称得的结果分别为1.6380g和0.1637g,那么称量 结果的绝对误差可以计算出来: 绝对误差(1=1.6380-1.6381=-0.0001(g) 绝对误差(2=0.1637-0.1638=一0.0001(g) 相对误差(E)1= -0.0001 ×100%=-0.006% 1.6381 相对误差(E2= -0.0001 ×100%=-0.06% 0.1638 ◆相对误差反映出误差在真实值中所占的比例,衡量分析结 果的准确度更为确切
0.000 1 100% 0.006% 1.638 1 − × = − 0.000 1 100% 0.06% 0.163 8 − × = − 例如:两个物体,真实重量分别为: 例如:两个物体,真实重量分别为:1.6381 g 1.6381 g 1.6381 g 1.6381 g 1.6381 g 1.6381 g 1.6381 g 1.6381 g和0.1638 g,而我们所称得的结果分别为 ,而我们所称得的结果分别为1.6380 g 1.6380 g 1.6380 g 1.6380 g 1.6380 g 1.6380 g 1.6380 g 1.6380 g和0.1637 g 0.1637 g 0.1637 g 0.1637 g 0.1637 g 0.1637 g 0.1637 g 0.1637 g,那么称量 结果的绝对误差可以计算出来: 结果的绝对误差可以计算出来: 绝对误差(E) 11 =1.6380 - 1.6381 1.6381 1.6381 1.6381 1.6381 1.6381 1.6381 1.6381 = -0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 绝对误差(E) 22 =0.1637 - 0.1638 0.1638 0.1638 0.1638 0.1638 0.1638 0.1638 0.1638 = -0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 0.0001(g) 相对误差(Err) 22 = 相对误差(Err) 11 = � 相对误差反映出误差在真实值中所占的比例,衡量分析结 相对误差反映出误差在真实值中所占的比例,衡量分析结 果的准确度更为确切。 果的准确度更为确切
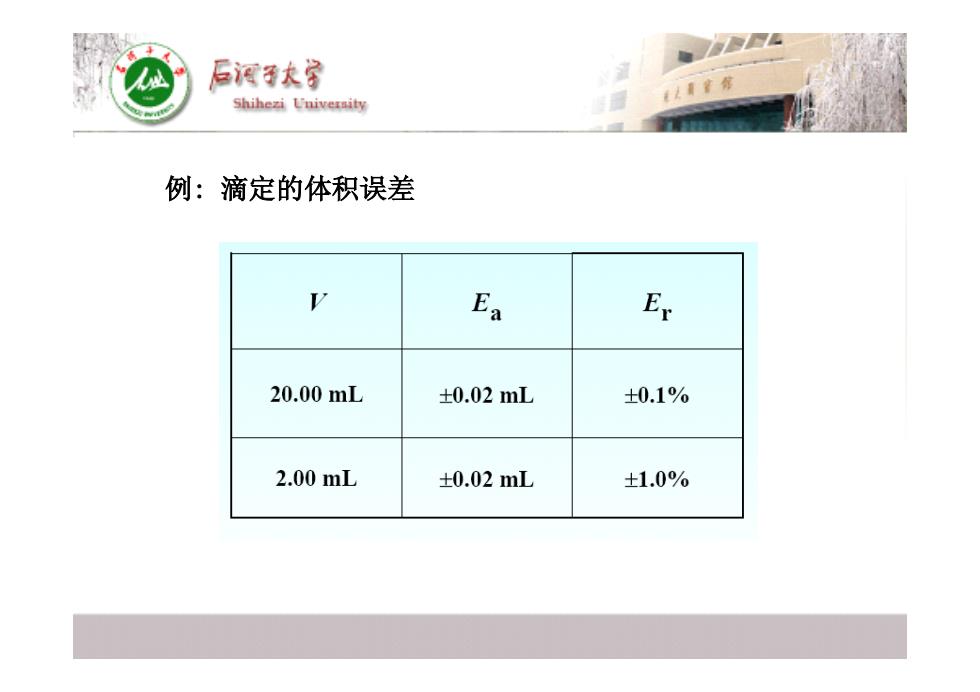
后润节水家 Shihezi University 例:滴定的体积误差 Ea Er 20.00mL ±0.02mL ±0.1% 2.00mL ±0.02mL ±1.0%
例: 滴定的体积误差 滴定的体积误差
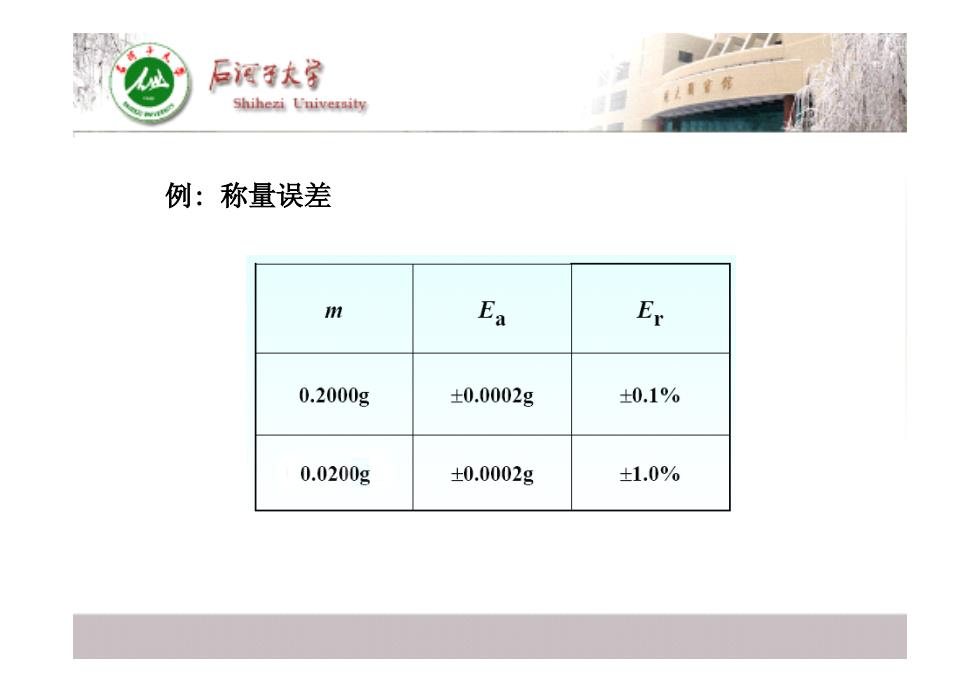
后酒子大 Shihezi Univeraity 例:称量误差 n Ea Er 0.2000g ±0.0002g ±0.1% 0.0200g ±0.0002g ±1.0%
例: 称量误差
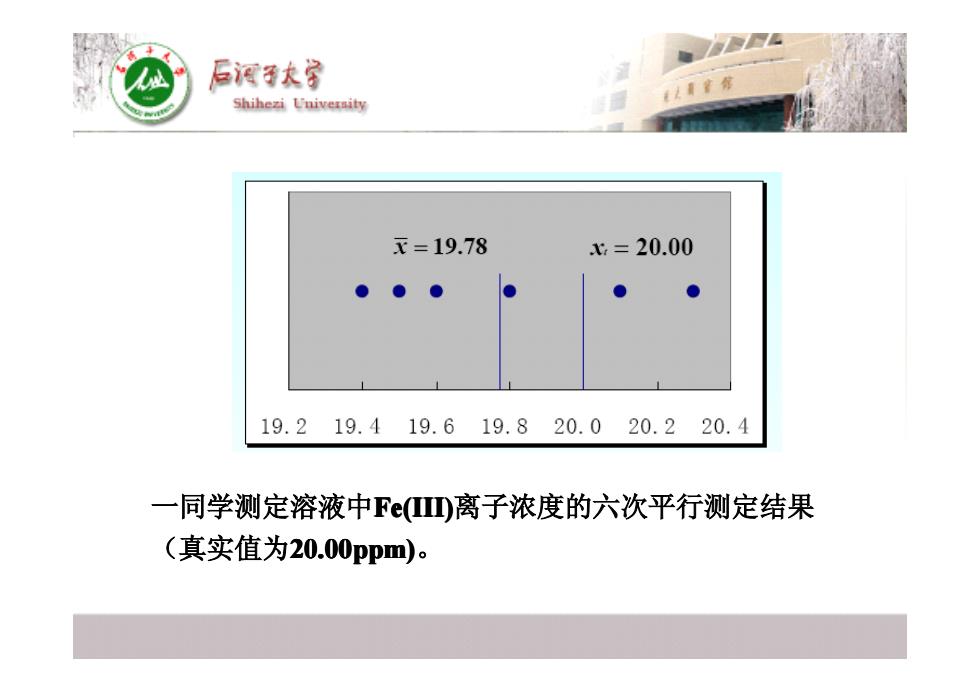
后酒子太 Shihezi University 元=19.78 x=20.00 ● ● ● 19.219.419.619.820.020.220.4 一同学测定溶液中F(四离子浓度的六次平行测定结果 (真实值为20.00ppm)
一同学测定溶液中 一同学测定溶液中Fe(III) Fe(III) Fe(III) Fe(III) Fe(III) Fe(III) Fe(III) Fe(III)离子浓度的六次平行测定结果 离子浓度的六次平行测定结果 (真实值为20.00ppm) 20.00ppm) 20.00ppm) 20.00ppm) 20.00ppm) 20.00ppm) 20.00ppm) 20.00ppm)

酒节大家 Shihezi University 2.精密度Precision):平行测定结果相互靠近的程度, 用偏差衡量。P43、41 1)偏差:测量值与平均值的差值,用d表示 d=x1-x 2)算术平均值:无=古+++七=台 口如果不取绝对值,各个偏差之和等于零: ∑d:=0
1)偏差: 测量值与平均值的差值,用 测量值与平均值的差值,用 d 表示 d = x i − x 2)算术平均值: )算术平均值: n x n x x x x n i i n ∑ = = + + + = 1 2 ⋯ 1 � 如果不取绝对值,各个偏差之和等于零: 如果不取绝对值,各个偏差之和等于零: ∑di = 0 2. 精密度(Precision) (Precision) (Precision) (Precision) (Precision) (Precision) (Precision) (Precision):平行测定结果相互靠近的程度, 平行测定结果相互靠近的程度, 用偏差衡量。P43、 41