
算法设计与分析〉算法概述>算法的复杂性 2).渐进性态的阶 设fN)和g(N)是定义在正整数集上的正函数, (1)大O表示法(算法运行时间的上限) 若存在正常数c和自然数N,使得当N≥N,时,有f)≤cg(N) 则称函数N)在N充分大时有上界,且g(N)是它的一个上界, 记为f(W)=O(g(N)),也称fN)的阶不高于g(N)的阶. 例如3n=0(n),n+1024=0(n), 2n2+11n-10=0(n2) n2=0(n3)?n3=0(n2)? 又如算法1-1中 Tmin (m)-2a+3t,Tmin (m)=0(1) Tmax(m)=(m+1)a+(2m+1)t+(m-l)s, Tmaa(m)=O(m) 18
18 算法设计与分析 > 算法概述 >算法的复杂性 2).渐进性态的阶 又如算法1-1中 Tmin (m)=2a+3t, Tmax(m)=(m+1)a+(2m+1)t+(m-1)s, Tmin (m)=O(1) Tmax(m)=O(m) 例如 3n=O(n), n+1024=O(n), n 2=O(n3 ) ? n 3=O(n2 ) ? 2n2+11n-10=O(n2 ) 若存在正常数c和自然数N0 使得当 N N0 时,有f(N)cg (N) 则称函数 f(N )在N充分大时有上界, 且 g(N)是它的一个上界, 记为 f(N) =O(g (N) ) , 也称 f(N) 的阶不高于g (N) 的阶. 设f(N)和 g (N) 是定义在正整数集上的正函数, (1)大O表示法 (算法运行时间的上限 )

算法设计与分析〉算法概述>算法的复杂性 1.O(f+0(g)=0(max(f,g) 2.0(f0+0(g)=0(f+g) 算 3.0(f0(g)=0(fg) 法 4.如果g(n)=0(f(n),则0()+0(g)=0() 则 5.f=0(f 6.O(cf(n)=0(f(n) 例如估计如下二重循环算法在最坏情况下时间复杂性T()的阶. for i:=1 to n do for j:=1 to i do {s1,s2,s3,s4;s1,s2,s3,s4为单一赋值语句 分析:内循环体只需0(1)时间故 内循环共需】 o0=02)=00 外循环共需 立o0=02)=0y+D)=0N) 19
19 算法设计与分析 > 算法概述 >算法的复杂性 例如 估计如下二重循环算法在最坏情况下时间复杂性T(n)的阶. 分析:内循环体只需O(1)时间,故 for i:= 1 to n do for j:=1 to i do {s1,s2,s3,s4} ; //s1,s2,s3,s4为单一赋值语句 = i j 1 O(1) O( 1) O( ) 1 i i j = = = 外循环共需 ) O(N ) 2 ( 1) O( ) O( ) O( 2 1 N 1 = + = = = = N N i i N i i 1. O(f)+O(g)=O(max(f,g)) 2. O(f)+O(g)=O(f+g) 3. O(f)·O(g)=O(f·g) 4. 如果 g(n)=O(f(n)),则 O(f)+O(g)=O(f) 5. f=O(f) 6. O(cf(n))=O(f(n)) 运 算 法 则 内循环共需

算法设计与分析〉算法概述>算法的复杂性 (2)大2表示法 (算法运行时间的下限) 如果3正常数c和自然数N使得当N≥N,时,有fN)≥cg(N) 则称函数fN)在N充分大时有下限,且g(N)是它的一个下限,记 为fN)=2(g())也称f(N)的阶不低于gN)的阶。 (3)0表示法 fN)=0(g(N))当且仅当fN)=O(g(N))且fN)=2(g(N)) 称函数fN)与g(N)同阶. 算法的渐进复杂性的阶对于算法的效率有着决定性的意义: 多项式阶算法(有效算法):时间复杂性与规模W的幂同阶, 指数阶算法:时间复杂性与规模W的一个指数函数同阶. 最优算法:时间复杂性达到其下界的算法 20
20 算法设计与分析 > 算法概述 >算法的复杂性 (2)大表示法 (算法运行时间的下限) f(N) =(g(N)) 当且仅当 f(N) =O(g (N)) 且f(N)=(g (N)) 称函数f(N)与g (N)同阶. 算法的渐进复杂性的阶对于算法的效率有着决定性的意义: 多项式阶算法(有效算法):时间复杂性与规模N 的幂同阶. 指数阶算法:时间复杂性与规模N 的一个指数函数同阶. 最优算法:时间复杂性达到其下界的算法. 如果正常数c和自然数N0使得当 N N0 时, 有f(N)cg (N) 则称函数f(N)在N充分大时有下限, 且 g(N)是它的一个下限,记 为f(N) = (g (N) ) 也称f(N)的阶不低于g(N)的阶。 (3)表示法
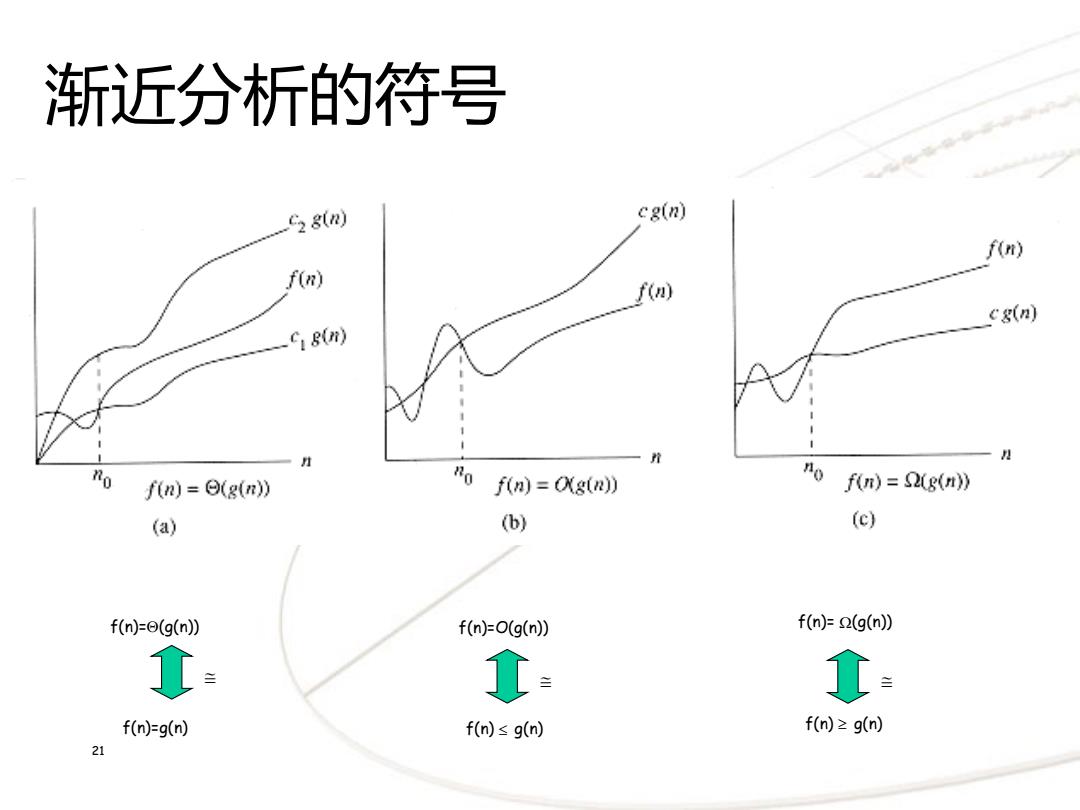
渐近分析的符号 C2 g(n) cg(n) f(n) f(n) f() c8(n) c1Bm) f(n)=e(g(n)) f(n)=Og(n)) no fn)=2e(r)》 (a) (b) (c) f(n)=@(g(n)) f(n)=O(g(n)) f(n)=2(g(n) t t t f(n)=g(n) f(n)≤g(n) f(n)≥g(n) 21
21 f(n)=(g(n)) f(n)=g(n) f(n)=O(g(n)) f(n) g(n) f(n)= (g(n)) f(n) g(n) @ @ @ 渐近分析的符号