
§4.1点源函数法回顾 §4格林函数 :M0(π-Tε).在T-tε中8(M-Mo)=0 于是 aδ(M-Modr=0 -T 右边: :由△G=-δ(M-M。)→G= 4元1 P-M,到M的距离 在0。 G(M,Mo)= 4元8 (:此时M,到oe上任一点M的距离为e)
§4.1 点源函数法回顾 §4 格林函数
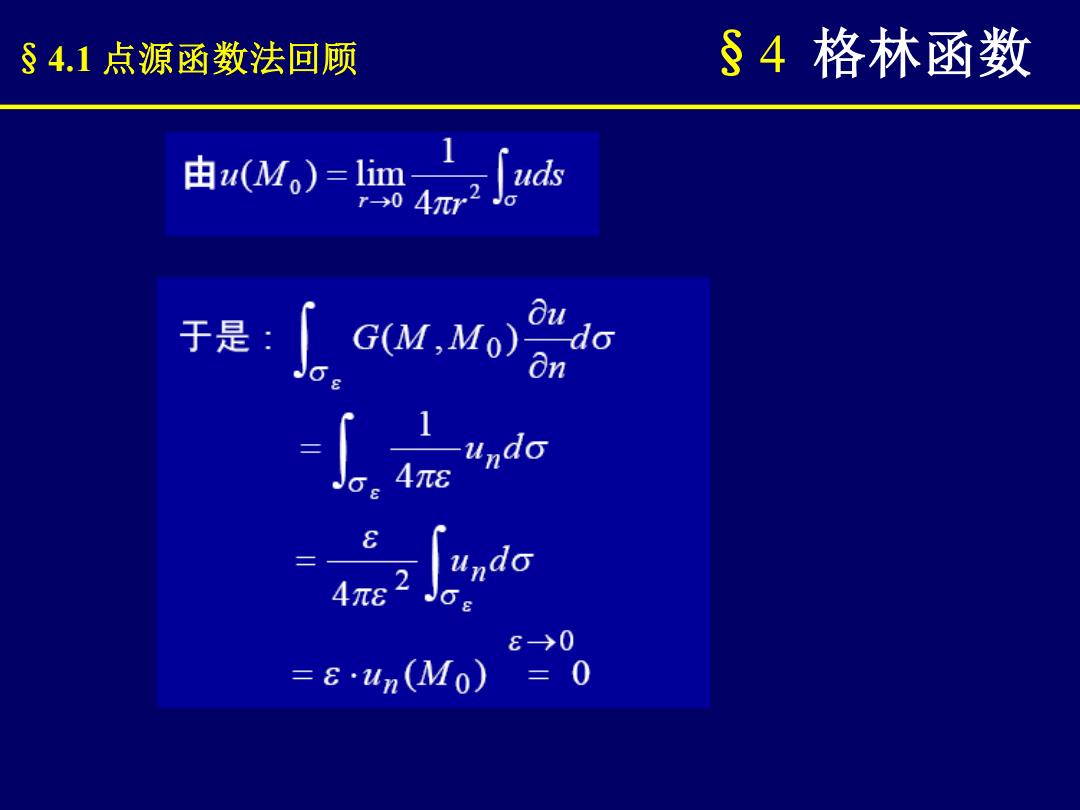
§4.1点源函数法回顾 §4格林函数 由w,)g咖 于是 oudo -起a 加 8→0 =eun(M0)=0
§4.1 点源函数法回顾 §4 格林函数

§4.1点源函数法回顾 §4格林函数 负号来自内小球面的 法向与矢径方向相反 ludou(M) e→0 于是有: )dc-aM。)=-Jj∬G(M,M,Mdr
0 0 ( ) ( ) ( , ) ( ) u G G u d u M G M M h M d n n − − = − 于是有: §4.1 点源函数法回顾 §4 格林函数 负号来自内小球面的 法向与矢径方向相反

§4.1点源函数法回顾 §4格林函数 于是:(Mo)=GM,Mo)bMMr -Icx.Mo0ao-n2c 上式的物理意义很难解释清楚,右边第一项,G(M,Mo) 代表M点的点源在M点产生的场,而h(M)代表的却是M 点的源。 注意到格林函数的对称性:G(M,M)=G(Mo,M) 将上式中的G(Mo,M用G(M,Mo)代替且,将M和M在公式 中互换,可得
§4.1 点源函数法回顾 §4 格林函数 注意到格林函数的对称性: 0 0 G M M G M M ( , ) ( , ) = 上式的物理意义很难解释清楚,右边第一项,G(M,M0 ) 代表M0点的点源在M点产生的场,而h (M)代表的却是M 点的源。 将上式中的G(M0 ,M)用G(M,M0 )代替且,将M和M0在公式 中互换,可得

§4.1点源函数法回顾 §4格林函数 u(M)=G(M,M)h(M)dro -cax号a-了以&au 基本积分公式 (4) 其中,dxo,do,分别表示在区域x中体分布源和o面分布源 内对M,取体积元和面积元。 表示对M求导。 Ono
§4.1 点源函数法回顾 §4 格林函数 (4) 0 0 0 0 ,d M M n 其中, 0 d 分别表示在区域 中体分布源和 面分布源 内对 取体积元和面积元。 表示对 求导。 0 0 0 0 0 0 0 0 0 0 ( ) ( , ) ( ) ( , ) ( ) ( , ) u M G M M h M d u G M M d u M G M M d n n = + −