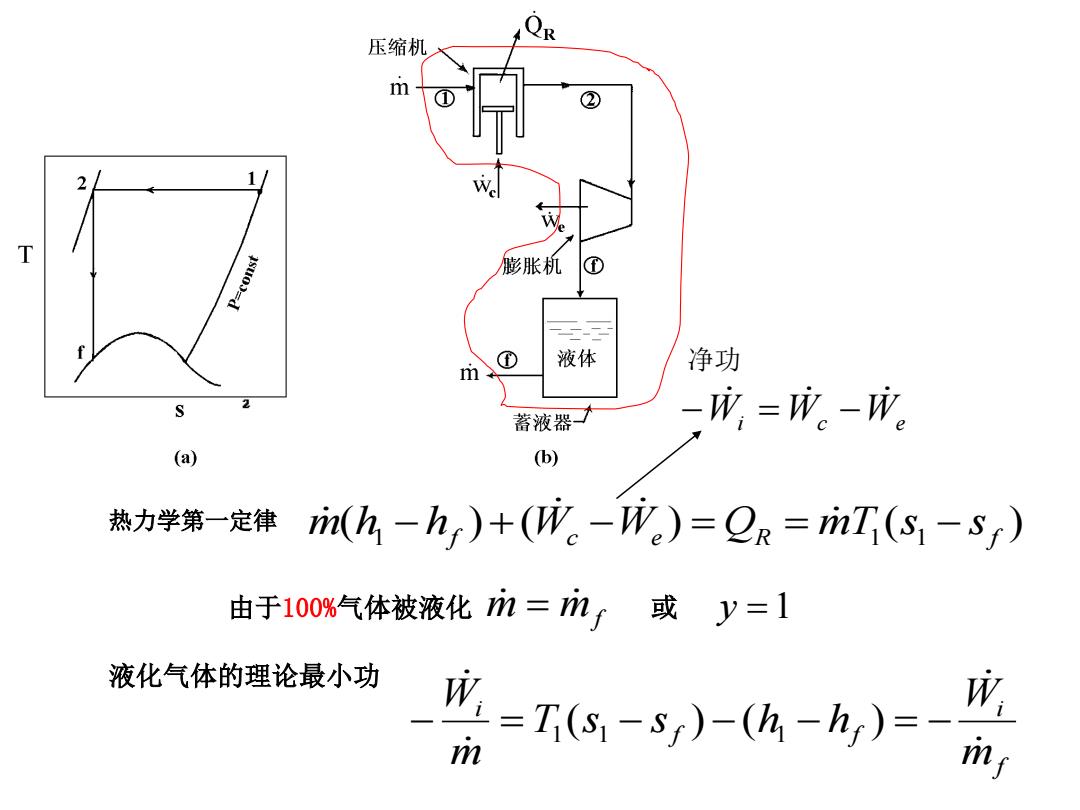
压缩机 m 2 1/ T P=const 膨胀机 液体 m 净功 蓄液器了 -成,=成。-成。 (a) (b) 热力学第一定律 rin(h-h)+W-W)=Og=rinT (s-s) 由于100%气体被液化m=mf或y=1 液化气体的理论最小功 =T5-sy)-(4-h,)= 成 m mf
热力学第一定律 ( ) ( ) ( ) 1 f c e R 1 1 f m h h W W Q m T s s Wi Wc We 净功 由于100%气体被液化 m m f 或 y 1 液化气体的理论最小功 f i f f i m W T s s h h m W 1 ( 1 ) ( 1 )
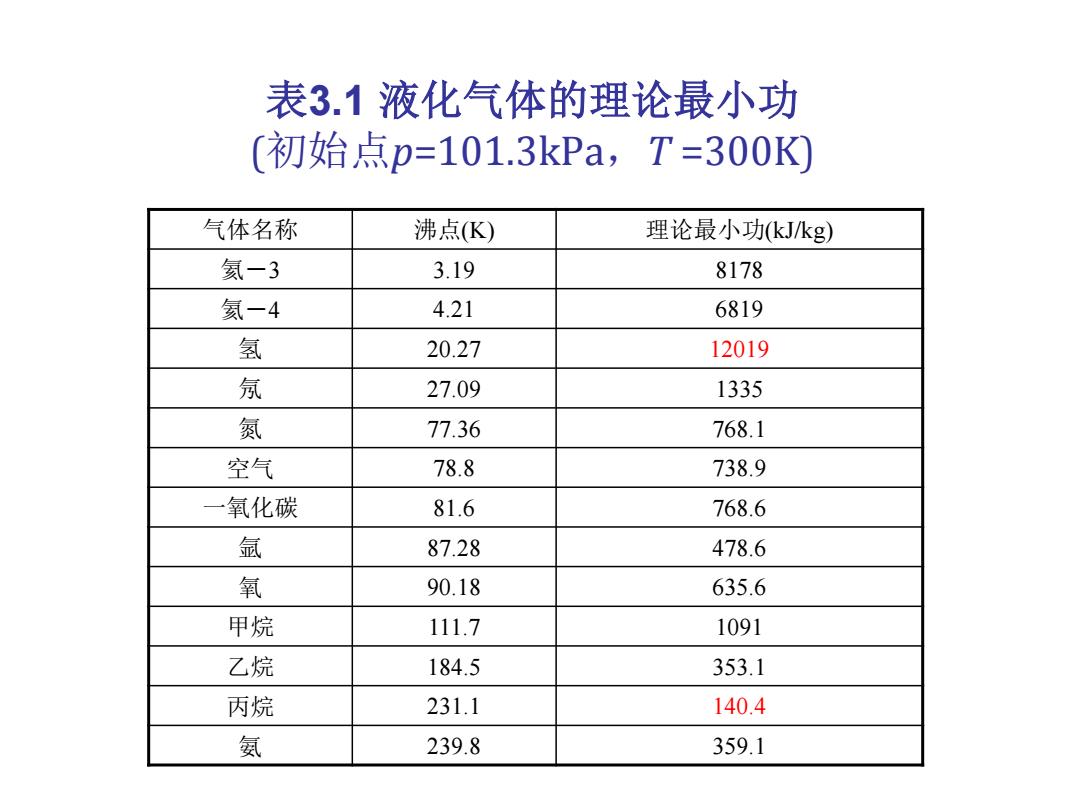
表3.1液化气体的理论最小功 (初始点p=101.3kPa,T=300K 气体名称 沸点(K) 理论最小功(kJkg) 氦一3 3.19 8178 氦-4 4.21 6819 氢 20.27 12019 氖 27.09 1335 氮 77.36 768.1 空气 78.8 738.9 一氧化碳 81.6 768.6 氩 87.28 478.6 氧 90.18 635.6 甲烷 111.7 1091 乙烷 184.5 353.1 丙烷 231.1 140.4 氨 239.8 359.1
表3.1 液化气体的理论最小功 (初始点p=101.3kPa,T =300K) 气体名称 沸点(K) 理论最小功(kJ/kg) 氦-3 3.19 8178 氦-4 4.21 6819 氢 20.27 12019 氖 27.09 1335 氮 77.36 768.1 空气 78.8 738.9 一氧化碳 81.6 768.6 氩 87.28 478.6 氧 90.18 635.6 甲烷 111.7 1091 乙烷 184.5 353.1 丙烷 231.1 140.4 氨 239.8 359.1
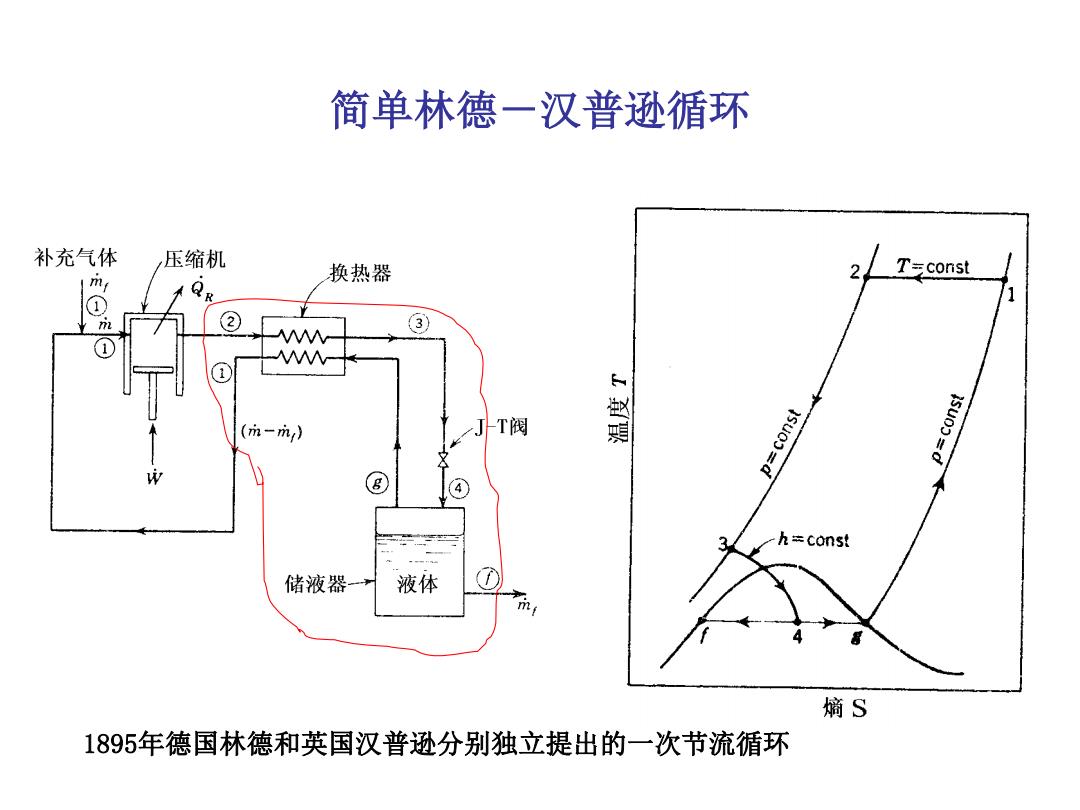
简单林德一汉普逊循环 补充气体 压缩机 换热器 2 T=const m. ② (m-m) JT阀 p=const p=const 4 h÷const 储液器→ 液体 熵S 1895年德国林德和英国汉普逊分别独立提出的一次节流循环
简单林德-汉普逊循环 1895年德国林德和英国汉普逊分别独立提出的一次节流循环
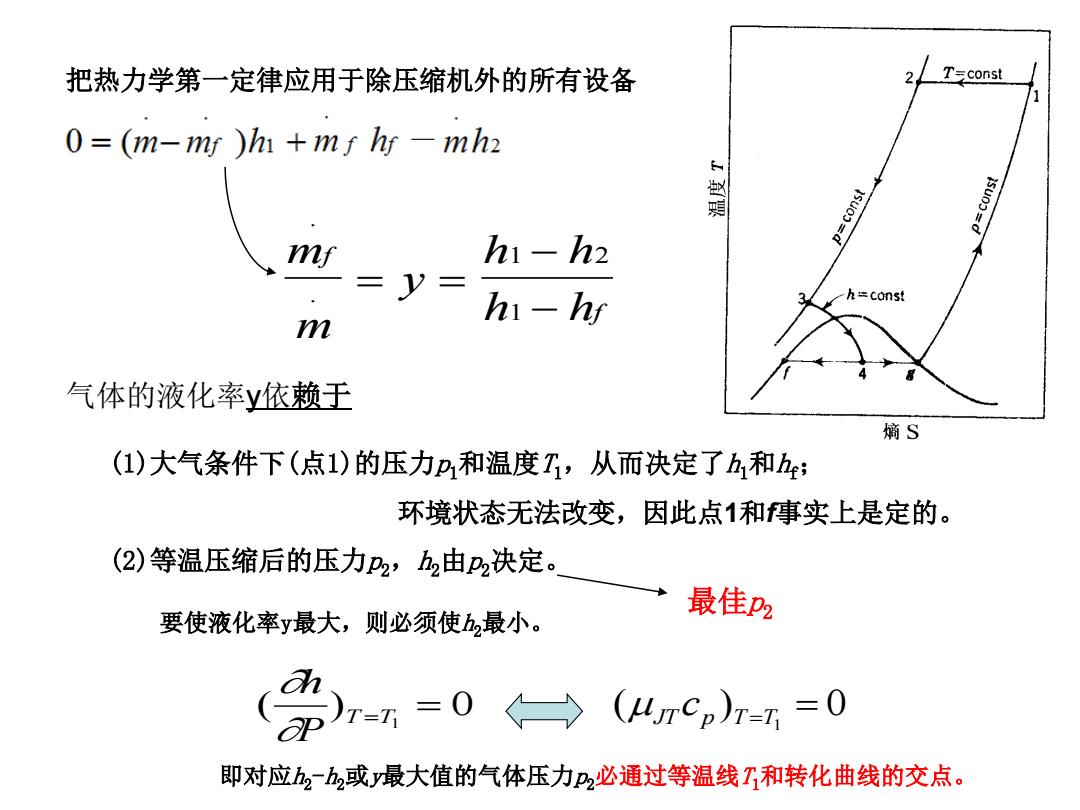
把热力学第一定律应用于除压缩机外的所有设备 T=const 0=(m-ms )h +ms hs -mh2 p=const p=const mf h1-h2 =y= hi-hf h=const m 气体的液化率y依赖于 熵S (1)大气条件下(点1)的压力p和温度T,从而决定了h和h: 环境状态无法改变,因此点和事实上是定的。 (2)等温压缩后的压力P2,2由P2决定。 要使液化率y最大,则必须使h最小。 最佳pP2 )==0→( (unrCp)T=T =0 即对应2-h2或y最大值的气体压力p2必通过等温线T和转化曲线的交点
把热力学第一定律应用于除压缩机外的所有设备 m m y h h h h f . . f 1 2 1 气体的液化率y依赖于 (1)大气条件下(点1)的压力p1和温度T1,从而决定了h1和hf; (2)等温压缩后的压力p2,h2由p2决定。 最佳p2 要使液化率y最大,则必须使h2最小。 环境状态无法改变,因此点1和f事实上是定的。 ( ) 0 1 T T P h ( ) 0 1 JT cp T T 即对应h2-h2或y最大值的气体压力p2必通过等温线T1和转化曲线的交点
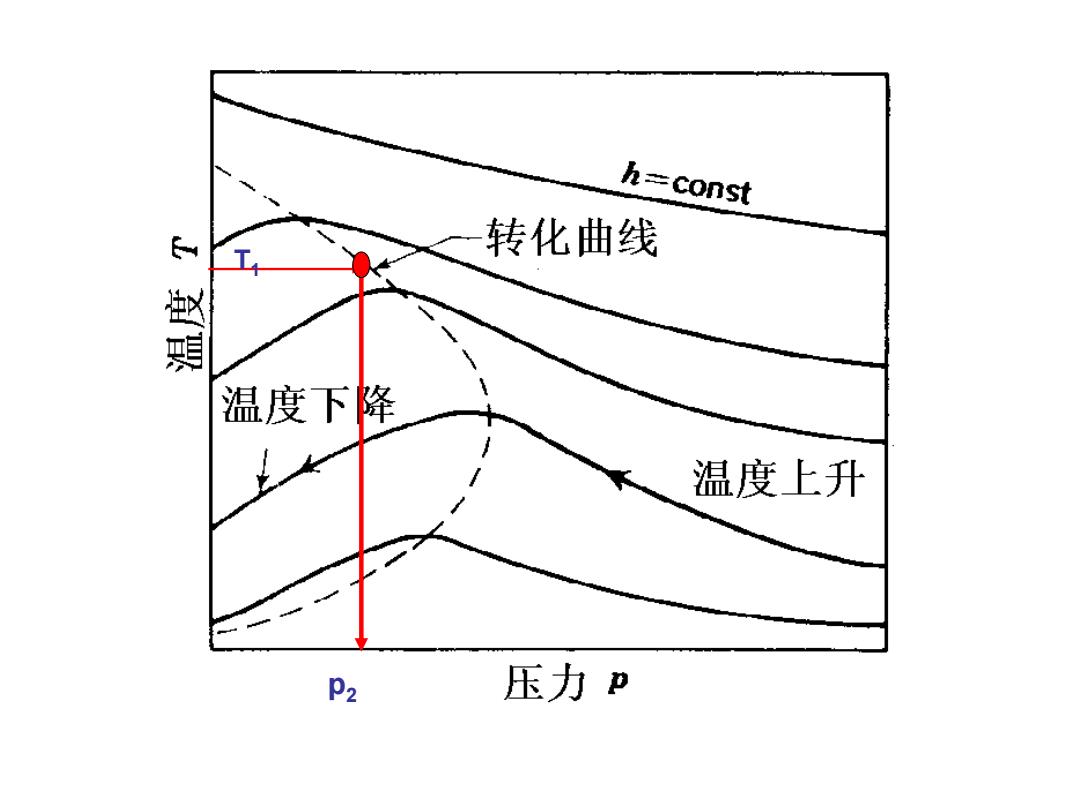
h=const 转化曲线 温度下降 温度上升 P2 压力p
T1 p2