
定态薛定谔方程 如果势场不显含时间 V(,t)=V( .分离变量y(,)=pr)/(),代入h y=iy 再两边同时除以w(r,) 访 f()1 f(t)a p(r)八 2+r p() ·左边只是时间函数,右边只是的函数→共同常数E 求解时间部分,可得f()=eh 定态薛定谔方程 16 X.J.WU@USTC
定态薛定谔方程 如果势场不显含时间 ( ) ( ) ( ) ( ) ( ) 2 1 2 2 i f t V f t t m = − + r r r • 左边只是时间函数,右边只是r的函数 → 共同常数E 定态薛定谔方程 𝑉 𝑟 Ԧ ,𝑡 = 𝑉(𝑟 Ԧ) − 𝜂 2 2𝑚 𝛻 2 + 𝑉 𝑟 Ԧ 𝜓 𝑟 Ԧ = 𝐸𝜓 𝑟 Ԧ 16 X. J. WU @ USTC

N粒子体系 E.工工5k小 ip》-Σ然+Σ,c小o》-p》 >17 X.J.WU@USTC
N粒子体系 ( ) 2 , 2 i tot ij i j i i j i p E V r r m = + ( ) ( ) ( ) ( ) 2 2 ˆ , 2 i i ij i j i i i i j i H r V r r r E r m = − + = 17 X. J. WU @ USTC

定态薛定谔方程一 势箱中的粒子 一维势箱中的粒子 (x) (无限深势阱,束缚态) 势函数 Ⅱ Ⅲ 0 (0<x<a) V(x)= 00 (x≥a,x≤0) 0 a 定态薛定谔方程 i= 方2d2 2m dx2 +V(x) >18 X.J.WU@USTC
V(x) x 0 a I II III = ( , 0) 0 (0 ) ( ) x a x x a V x 一维势箱中的粒子 (无限深势阱,束缚态) 定态薛定谔方程 —— 势箱中的粒子 ( ) 2 ˆ 2 2 2 V x dx d m H = − + 定态薛定谔方程 势函数 18 X. J. WU @ USTC
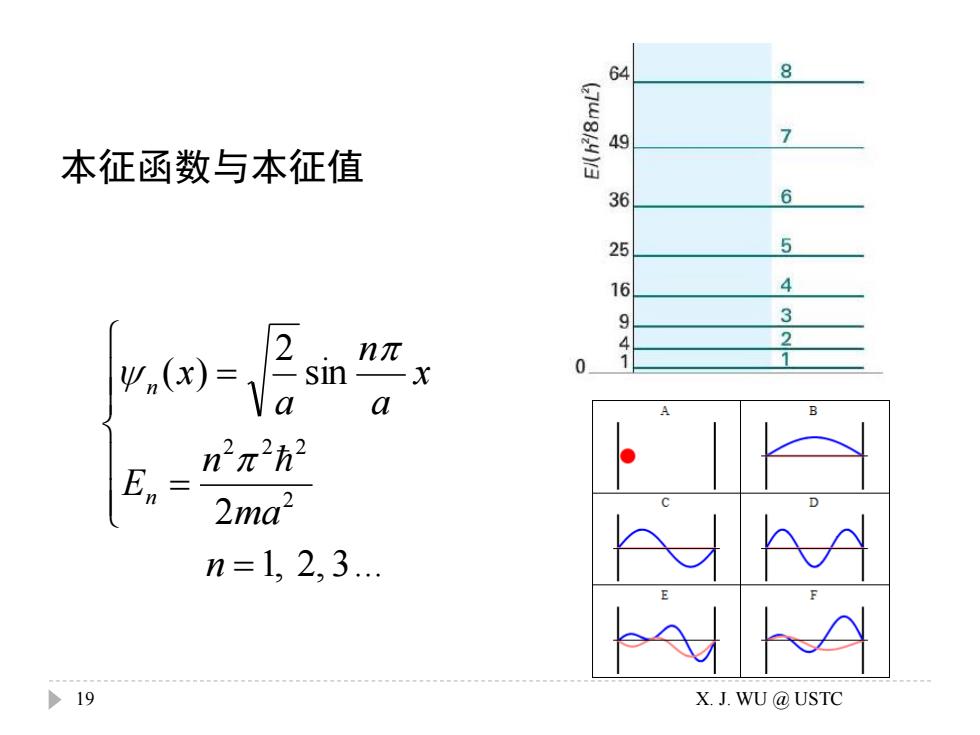
64 8 49 7 本征函数与本征值 36 6 25 5 16 4 9 3 2 .nπ 2 0 1 sin- Va a n'n'h2 En= 2ma? n=1,2,3. >19 X.J.WU@USTC
1, 2, 3. 2 sin 2 ( ) 2 2 2 2 = = = n ma n E x a n a x n n 本征函数与本征值 19 X. J. WU @ USTC

应用:离域键的形成 1,3丁二烯(C=C-C=C,键长为a) 2k2 n2h2 2m 8ma2 ·模型1:两个孤立双键 4 E0=4E= h 3 2ma2 2 ·模型2:一个离域大π键 Em=2(E+E)=1+4n 5h2 4m(3a)236ma2 4 3 E'ot<Erot 易于形成大π键 2 >20 X.J.WU@USTC
应用:离域键的形成 • 模型1:两个孤立双键 • 模型2:一个离域大 键 20 X. J. WU @ USTC