
为重要的统计指数。静态指数则是动态指数在实际应用中的扩展 5.按照常用的计算总指数的方法或形式可以分 以数量上表明不能直接相加的社 经济现象的总指数 平均指数 一以个体指数为基础,采取平均形式编制的总指数。 4.2.4编制指数的关键问题 编制总指数可以考虑两种方式。 一是先综合后对比,二是先对比后平均 1.先综合 后对比的方式 如果我们知道某几种商品价格和销售量资料,研究全部商品的价格和销售量变动情况 首先将各种商品的价格或销售最资料加总起来,然后通过对比得到相应的总指数,这种方法 通常称为综合(总和)指数法。此时我们会遇到这样两个问题,一是不同商品的数量和价格 不能直接加总,或者说,直接加总的结果没有实际经济含义:二是简单综合法编制的指数明 显地受到高品计量单位的影响。因此,简单综合指数难以成为现象变动程度的一种客观测度, 商品的价格或销售量都 4不 同度量”的现 们构成 不能直接加总的“复列 现象总体”,倘若不解决有关现象的同度量问题就将其直接加总,显然难以得到适当的指数 计算结果。 2.先对比、后平均的方式 首先将各种商品的价格或销售量资料进行对比(计算个体指数),然后通过个体指数的 平均得到相应的总指数 ,这种方法通常称为“平均指数法”。这样当我们将各 商品的个 指数作简单平均时,没有适当地考虑不同商品的重要性程度。从经济分析的角度看,各种商 品的重要性程度是有差异的,简单平均指数不能反映这种差异,因而难以满足分析的要求。 归纳起来,简单综合指数与简单平均指数都存在方法上的缺陷。但是,迄今为止,综合 指数法与平均指数法仍然是编制统计指数的两个基本方法。为了运用综合法编制总指数,必 须首先考虑被比较的诸现象是否同度最、怎样同度量的问题:因此,编制综合指数的基本问 题是 “同度量”的问题,解决这 问题的方法就是编制加权综合指数。而为了运用平均法线 制总指数,又必须首先考虑被比较诸现象的重要性程度是否相同、怎样衡量的问题(此外, 还有选择何种平均数形式的问题):因此,编制平均指数的基本问题之一是合理加权的问题, 解决这一问题的方法就是编制加权平均数。 4.3加权指数 4.3.1加权综合指数 加权综合指数(Weighted aggregative index number)是通过加权来测定一组项目的 综合变动状况。若所测定的是一组项目的物量变动状况,称为数量指标指数,如产品产量指 数、商品销售量指数 等 :若所测定的是一组项目的质量变动状况,则称为质量指标指数, 如 价格指数、产品成本指数等。但由于权数可以固定在不同时期,因而加权综合指数有不同的 计算公式, 1.基期变量值加权 基期变最值加权是指在计算一组项目的综合指数时,把作为权数的各变量值固定在基期 来计算指数。早在1864年,德国学者拉斯贝尔斯(Las S)就曾提出用基期消费量加权 来计算价格指数 指数 拉氏指 或L式指数。拉氏加权法可推广到其他指数的 算。基期变量值加权的拉氏质量指标指数和数量指标指数的一般计算公式为:
11 为重要的统计指数。静态指数则是动态指数在实际应用中的扩展。 5.按照常用的计算总指数的方法或形式可以分为 综合指数——从数量上表明不能直接相加的社会经济现象的总指数。 平均指数——以个体指数为基础,采取平均形式编制的总指数。 4.2.4 编制指数的关键问题 编制总指数可以考虑两种方式。一是先综合后对比,二是先对比后平均。 1.先综合、后对比的方式 如果我们知道某几种商品价格和销售量资料,研究全部商品的价格和销售量变动情况。 首先将各种商品的价格或销售量资料加总起来,然后通过对比得到相应的总指数,这种方法 通常称为综合(总和)指数法。此时我们会遇到这样两个问题,一是不同商品的数量和价格 不能直接加总,或者说,直接加总的结果没有实际经济含义;二是简单综合法编制的指数明 显地受到商品计量单位的影响。 因此, 简单综合指数难以成为现象变动程度的一种客观测度, 因为不同商品的价格或销售量都是“不同度量”的现象,它们构成了不能直接加总的“复杂 现象总体” ,倘若不解决有关现象的同度量问题就将其直接加总,显然难以得到适当的指数 计算结果。 2.先对比、后平均的方式 首先将各种商品的价格或销售量资料进行对比(计算个体指数),然后通过个体指数的 平均得到相应的总指数,这种方法通常称为“平均指数法” 。这样当我们将各种商品的个体 指数作简单平均时,没有适当地考虑不同商品的重要性程度。从经济分析的角度看,各种商 品的重要性程度是有差异的,简单平均指数不能反映这种差异,因而难以满足分析的要求。 归纳起来,简单综合指数与简单平均指数都存在方法上的缺陷。但是,迄今为止,综合 指数法与平均指数法仍然是编制统计指数的两个基本方法。为了运用综合法编制总指数,必 须首先考虑被比较的诸现象是否同度量、怎样同度量的问题;因此,编制综合指数的基本问 题是“同度量”的问题,解决这一问题的方法就是编制加权综合指数。而为了运用平均法编 制总指数,又必须首先考虑被比较诸现象的重要性程度是否相同、怎样衡量的问题(此外, 还有选择何种平均数形式的问题);因此, 编制平均指数的基本问题之一是合理加权的问题, 解决这一问题的方法就是编制加权平均数。 4.3 加权指数 4.3.1 加权综合指数 加权综合指数(Weighted aggregative index number)是通过加权来测定一组项目的 综合变动状况。若所测定的是一组项目的物量变动状况,称为数量指标指数,如产品产量指 数、商品销售量指数等;若所测定的是一组项目的质量变动状况,则称为质量指标指数,如 价格指数、产品成本指数等。但由于权数可以固定在不同时期,因而加权综合指数有不同的 计算公式。 1.基期变量值加权 基期变量值加权是指在计算一组项目的综合指数时, 把作为权数的各变量值固定在基期 来计算指数。早在 1864 年,德国学者拉斯贝尔斯(Laspeyres)就曾提出用基期消费量加权 来计算价格指数,这一指数被称为拉氏指数或 L 式指数。拉氏加权法可推广到其他指数的计 算。基期变量值加权的拉氏质量指标指数和数量指标指数的一般计算公式为:
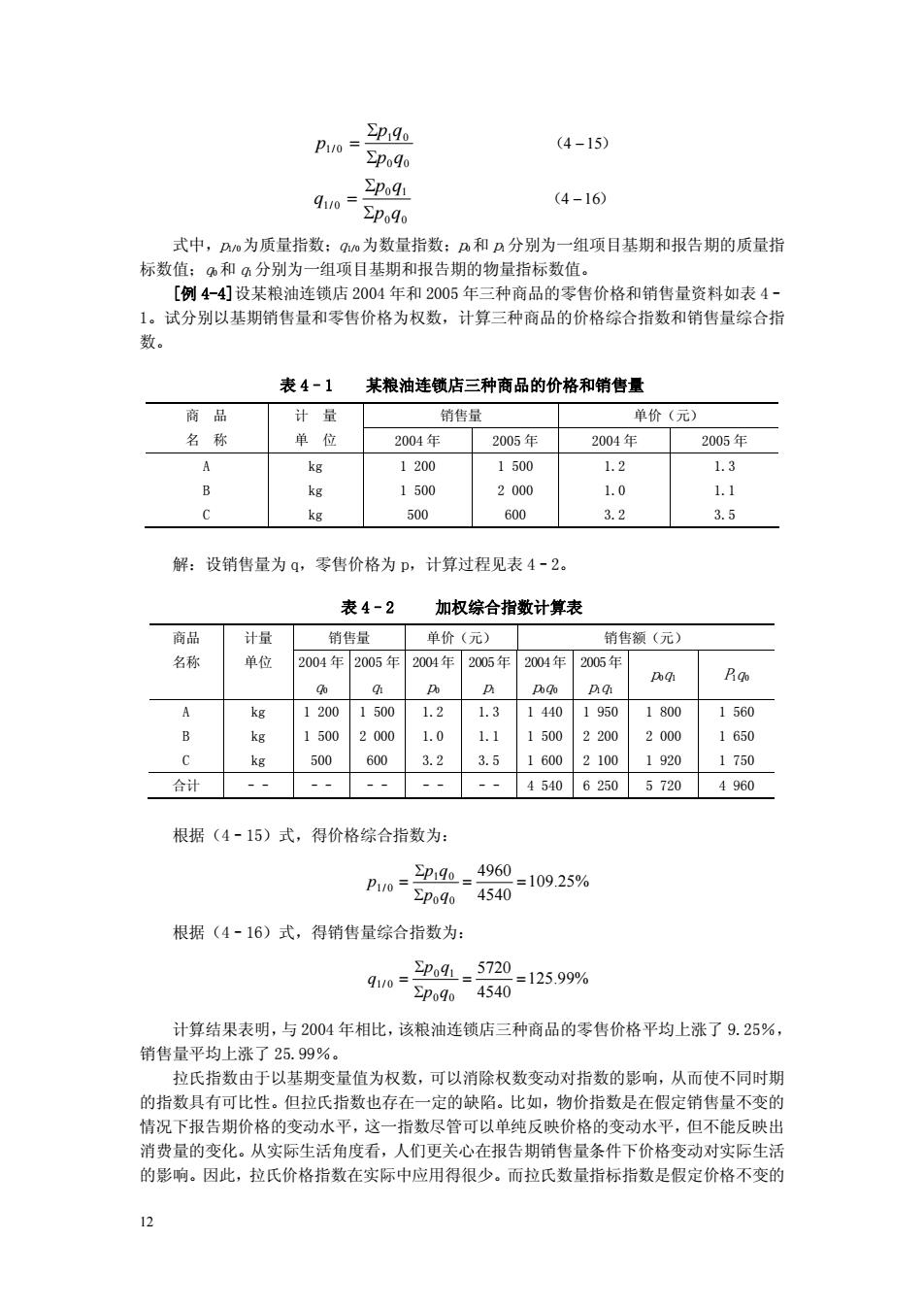
Pin =29 (4-15) 910= P41 (4-16) 式中,m为质量指数:q为数量指数:m和n分别为一组项目基期和报告期的质量指 标数值:0和分别为一组项目基期和报告期的物量指标数值。 [例4-4]设某粮油连锁店2004年和2005年三种商品的零售价格和销售量资料如表4- 1。试分别以基期销售量和零售价格为 权数 计算 种商品的价格综合指数和销售量综合指 数。 表4-1 某粮油连锁店三种商品的价格和销售量 计量 销售量 单价《元) 名 单位 2004年 2005年 2004年 2005年 kg 1200 1500 1.2 1.3 B 1500 2000 1.0 11 500 600 3.2 3.5 解:设销售量为4,零售价格为P,计算过程见表4-2。 表4-2 加权综合指数计算表 销售量 单价(元) 销售额(元) 单代 2004 2005年 2004年 2005年 2004年205年 0 6 0 1200 1500 1.2 1.314401950 18001560 1500 2000 10 11 15002200 2000 1650 500 60 32 35 16002100 1920 1750 合计 -4540625057204960 根据(4-15)式,得价格综合指数为: Puo -29 4960 904540 =109.25% 根据(4-16)式,得销售量综合指数为: 4540=125.99% 5720 计算结果表明,与2004年相比,该粮油连锁店三种商品的零售价格平均上涨了9.25%, 销售量平均上涨了25.99%。 拉氏指数由于以基期变量值为权数,可以消除权数变动对指数的影响,从而使不同时期 的指数具有可比性。但拉氏指数也存在一定的缺陷。比如,物价指数是在假定销售量不变的 情况下报告期价格的变动水平 指数尽管可以单纯反映价格的变动水平,但不能反映出 消费量的变化。从实际生活角度看,人们更关心在报告期销售量条件下价格变动对实际生活 的影响。因此,拉氏价格指数在实际中应用得很少。而拉氏数量指标指数是假定价格不变的
12 ( ) ( ) 4 16 4 15 0 0 0 1 1/ 0 0 0 1 0 1/ 0 - - S S = S S = p q p q q p q p q p 式中,p1/0为质量指数;q1/0为数量指数;p0和 p1分别为一组项目基期和报告期的质量指 标数值;q0和 q1分别为一组项目基期和报告期的物量指标数值。 [例 4-4]设某粮油连锁店 2004 年和 2005 年三种商品的零售价格和销售量资料如表 4– 1。试分别以基期销售量和零售价格为权数,计算三种商品的价格综合指数和销售量综合指 数。 表 4–1 某粮油连锁店三种商品的价格和销售量 商 品 销售量 单价(元) 名 称 计 量 单 位 2004 年 2005 年 2004 年 2005 年 A B C kg kg kg 1 200 1 500 500 1 500 2 000 600 1.2 1.0 3.2 1.3 1.1 3.5 解:设销售量为 q,零售价格为 p,计算过程见表 4–2。 表 4–2 加权综合指数计算表 商品 销售量 单价(元) 销售额(元) 名称 计量 单位 2004 年 q0 2005 年 q1 2004年 p0 2005年 p1 2004年 p0q0 2005年 p1q1 p0q1 P1q0 A B C kg kg kg 1 200 1 500 500 1 500 2 000 600 1.2 1.0 3.2 1.3 1.1 3.5 1 440 1 500 1 600 1 950 2 200 2 100 1 800 2 000 1 920 1 560 1 650 1 750 合计 –– –– –– –– –– 4 540 6 250 5 720 4 960 根据(4–15)式,得价格综合指数为: 109. 25% 4540 4960 0 0 1 0 1/ 0 = = S S = p q p q p 根据(4–16)式,得销售量综合指数为: 125. 99% 4540 5720 0 0 0 1 1/ 0 = = S S = p q p q q 计算结果表明, 与 2004 年相比, 该粮油连锁店三种商品的零售价格平均上涨了 9.25%, 销售量平均上涨了 25.99%。 拉氏指数由于以基期变量值为权数,可以消除权数变动对指数的影响,从而使不同时期 的指数具有可比性。但拉氏指数也存在一定的缺陷。比如,物价指数是在假定销售量不变的 情况下报告期价格的变动水平, 这一指数尽管可以单纯反映价格的变动水平,但不能反映出 消费量的变化。从实际生活角度看,人们更关心在报告期销售量条件下价格变动对实际生活 的影响。因此,拉氏价格指数在实际中应用得很少。而拉氏数量指标指数是假定价格不变的