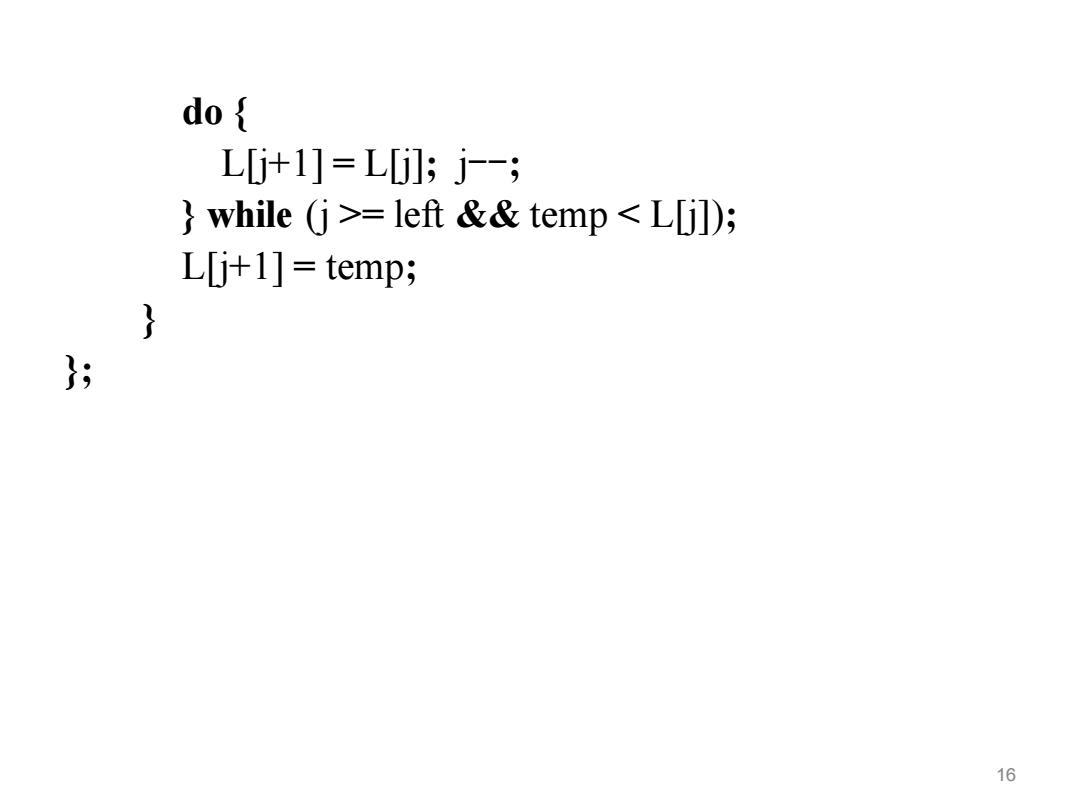
do L[+1]=L];j--; while (j>=left &temp L[jl); L[j+1]=temp; 3 ; 16
do { L[j+1] = L[j]; j--; } while (j >= left && temp < L[j]); L[j+1] = temp; } }; 16

·设待排序元素个数为currentSize=n,则该算法的主程序执 行-1趟。排序码比较次数和元素移动次数与元素排序码 的初始排列有关。 最好情况下,排序前元素已按排序码从小到大有序,每趟 只需与前面有序元素序列的最后一个元素比较1次,总的 排序码比较次数为-1,元素移动次数为0。 最坏情况下,第i趟时第i个元素必须与前面i个元素都做 排序码比较,并且每做1次比较就要做1次数据移动。则总 排序码比较次数KCN和元素移动次数RMN分别为 KCN 分i=mn-10/2≈r22, i=1 RMN=∑(i+2)=(n+4)(n-1)/2≈n2/2 i=1 平均情况下,排序的时间复杂度为O(2)。 直接插入排序是一种稳定的排序方法。 17
• 设待排序元素个数为currentSize = n, 则该算法的主程序执 行n-1趟。排序码比较次数和元素移动次数与元素排序码 的初始排列有关。 • 最好情况下,排序前元素已按排序码从小到大有序,每趟 只需与前面有序元素序列的最后一个元素比较1次,总的 排序码比较次数为 n-1, 元素移动次数为0。 • 最坏情况下, 第 i 趟时第 i 个元素必须与前面 i 个元素都做 排序码比较, 并且每做1次比较就要做1次数据移动。则总 排序码比较次数KCN和元素移动次数RMN分别为 • 平均情况下,排序的时间复杂度为 O(n 2 )。 • 直接插入排序是一种稳定的排序方法。 − = − = = + = + − = = − 1 1 1 1 2 4 1 2 2 1 2 2 n i n i RMN i n n n KCN i n n n ( ) ( )( )/ / ( )/ / , 2 2 17

折半插入排序(Binary Insert Sort) ·基本思想是: 设在顺序表中有一个元素序列V[0,V[1小,, V[n-1]。其中,VI0],Ⅵ1,,V[i-1]是已经排好 序的元素。在插入V[时,利用折半搜索法寻找 V[的插入位置。 18
折半插入排序 (Binary Insert Sort) • 基本思想是 : 设在顺序表中有一 个元素序列 V[0], V[1], …, V[n-1]。其中, V[0], V[1], …, V[i-1] 是已经排好 序的元素。在插入V[i] 时, 利用折半搜索法寻找 V[i] 的插入位置。 18

折半插入排序的算法 #include "dataList.h" template <class T> void BinaryInsertSort(dataList<T>&L, const int left,const int right) /利用折半搜索,在L.Vector[left到L.Vector[i--l]中 /查找L.Vector[i]应插入的位置,再进行插入。 Element<T>temp; int i,low,high,middle,k; for (i=left+1;i<=right;++) temp L[i];low left;high =i-1; while(low<=high){/折半搜索寻找插入位置 middle=(low+high)/2;/取中点 19
折半插入排序的算法 #include "dataList.h" template <class T> void BinaryInsertSort (dataList<T>& L, const int left, const int right) { //利用折半搜索, 在L.Vector[left]到L.Vector[i-1]中 //查找L.Vector[i]应插入的位置, 再进行插入。 Element<T> temp; int i, low, high, middle, k; for (i = left+1; i <= right; i++) { temp = L[i]; low = left; high = i-1; while (low <= high) { //折半搜索寻找插入位置 middle = (low+high)/2; //取中点 19

if (temp<L[middle]) /川插入值小于中点值 high=middle-l;/向左缩小区间 else low middle+1; 川否则,向右缩小区间 for (k=i-1;k>=low;k--L[k+1]=L[k]; 川成块移动,空出插入位置 L[low]temp; /川插入 }; 20
if (temp < L[middle]) //插入值小于中点值 high = middle-1; //向左缩小区间 else low = middle+1; //否则, 向右缩小区间 } for (k = i-1; k >= low; k--) L[k+1] = L[k]; //成块移动,空出插入位置 L[low] = temp; //插入 } }; 20