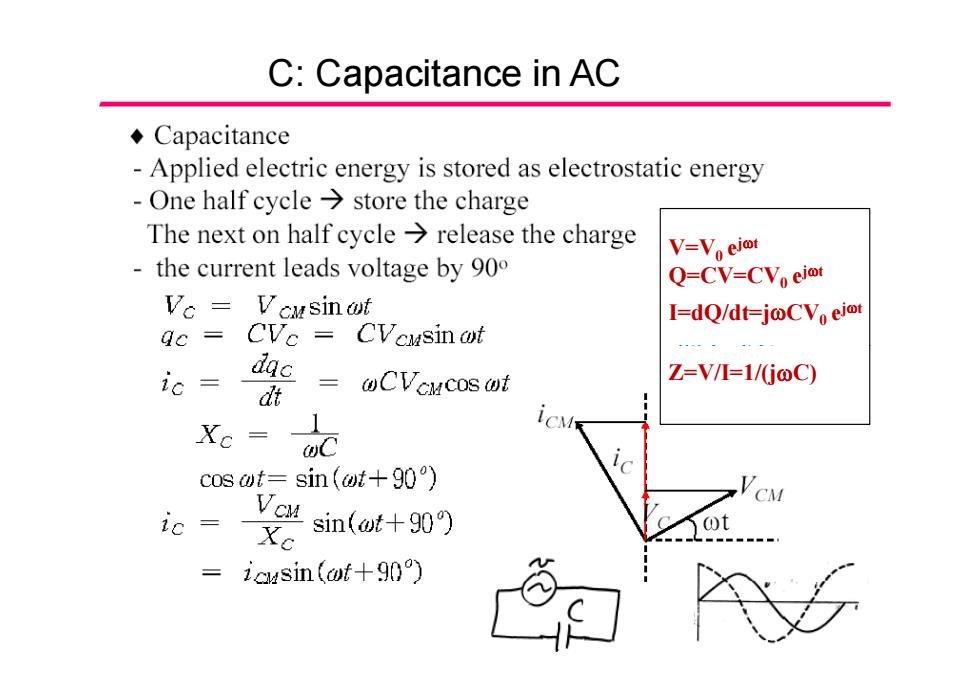
C:Capacitance in AC ◆Capacitance -Applied electric energy is stored as electrostatic energy -One half cycle>store the charge The next on half cycle>release the charge V=Vo ejot the current leads voltage by 900 Q=CV=CVoej@t Vo Vcusinot I=dQ/dt=joCVoeict gc CVc CVausinot ic da @CVCMcos @t Z=V/I=1/(j@C) dt XC cos of=sin (f+90) Vou C ic Xc sin(@t++90) icusin (of++90))
C: Capacitance in AC V=V0 ejt Q CV CV Q j t =CV =CV0 ejt I=dQ/dt=j CV0 ejt Z=V/I=1/(j C)

L:Inductance in AC I=Iejt e= -L dt V=LdI/dt=LInj@eicot d V V di = L L sinot Z=V/I=joL = VLM sin otd(ot) VLM L cosot XL= oL -cos ot=sin(ot-90) 江= X sin(@t-90) = iLusin (ot-90) LM
L: Inductance in AC I=I0 ejt V=L dI/dt=LI 0j ejt Z= V/I = j L

Complex impedance (impedance and admittance) L R IMPEDANCE ADMITTANCE CIRCUIT REAL IMAGINARY REAL IMAGINARY R - R 0 -I 0 1 000- 0 wL 0 C. 0 1 wC 0 wC
Complex impedance (impedance and admittance)

RC parallel circuit Y-R +jwC Z- 1 +C R Z- R CR2 1十a2CR2 1+0CR 1 W= 个 RC 频率走向 R 1+o2C2R2 R 2 Z"= @CR2 x— R 1+o2C2R2 Izicos(x) (a) (6 tan(0)=(-Z")/Z'=@CR 半圆:z-+z=
RC parallel circuit ' R Z 频率走向 2 2 2 1 ' C R Z 2 CR 2 2 2 1 " C R CR Z R 2 2 R 2 ) 2 ) " ( 2 ( ' R Z R tan( ) (Z")/ Z' CR 半圆:Z

Nyquist plot 1)Nyquist plot:-Z"vs.Z' 2)Characteristic frequency:=1/(RC) (maximum point) or time constant:t=RC 3)Frequency change direction 4)Components:semicircles straight lines
Nyquist plot 1) Nyquist plot: Nyquist plot: -Z” vs Z.’ 2) Characteristic freq y uenc : c = 1/(RC) c (maximum point) or time constant: = RC 3) Frequency change direction 4) Components: semicircles + straight lines