
Bool BinSrTree_Del(BiTree &BT,KeyType kval){ f=NULL: if(!BinSrTree(BT,kval,p,f)return FALSE;l∥不删除 if(p->IChild&&p->rChild){lW度为2,左右子树都非空 q=p;t=p->IChild: while (t->rChild){q=t;t=t->rChild;} p->data=t->data;∥t指向左子树中关键字最大的结点 if (q !p)q->rChild =t->IChild; else g->IChild=t->IChild;/t结点为p结点的左子树根 free(t); } else{W度<=1 q=p; p=(Ip->rChild)?p->IChild:p->rChild;∥右子树为空,挂其左子树 ∥否则挂其右子树 if()BT=p;∥删除的是根结点 elsefif(g==f->Ichild)f->Ichild=p;else f->rchild=p; delete q; M/BinSrTree_Del
Bool BinSrTree_Del(BiTree &BT, KeyType kval) { f = NULL; if (!BinSrTree(BT, kval, p, f)) return FALSE; // 不删除 if (p->lChild && p->rChild) { //度为2,左右子树都非空 q = p; t = p->lChild; while (t->rChild) { q = t; t = t->rChild;} p->data = t->data; // t指向左子树中关键字最大的结点 if (q != p) q->rChild = t->lChild; else q->lChild = t->lChild; // t结点为p结点的左子树根 free(t); } else { //度<=1 q = p; p= (!p->rChild) ? p->lChild: p->rChild; // 右子树为空,挂其左子树 // 否则挂其右子树 if(!f)BT=p; //删除的是根结点 else{if(q==f->lchild)f->lchild=p;else f->rchild=p; } delete q; } }// BinSrTree_Del

平衡三叉树 (AVL树) 。 什么是平衡二叉树 一树中每个结点的左、右子树深度之差的绝对值不 大于1,这种平衡状态的二叉查找树。 ·平衡因子 一结点的左子树深度和右子树深度之差。 - AVL树的平衡因子只能取-1,0,1 。 最小子树根 离插入结点最近且平衡因子不满足绝对值小于等 于1的祖先结点。 实现方法:平衡旋转技术 一四种平衡旋转方式 ypb@ustc.edu.cn 17 中国科学技术大学
ypb@ustc.edu.cn 17 中国科学技术大学 平衡二叉树(AVL树) • 什么是平衡二叉树 – 树中每个结点的左、右子树深度之差的绝对值不 大于1,这种平衡状态的二叉查找树。 • 平衡因子 – 结点的左子树深度和右子树深度之差。 – AVL树的平衡因子只能取-1,0,1 • 最小子树根 – 离插入结点最近且平衡因子不满足绝对值小于等 于1的祖先结点。 • 实现方法:平衡旋转技术 – 四种平衡旋转方式

B和BR深度 相等鸣? A B 2 0 A B 0 1 AR h-2 BL BL h-2 h- h-】 BR h-2 BR AR h-2 插入节点 LL型旋转
A 2 B 1 BL BR AR h-1 h-2 h-2 B 0 A 0 BR AR BL h-1 h-2 h-2 插入节点 LL型旋转 BL和BR深度 相等吗?
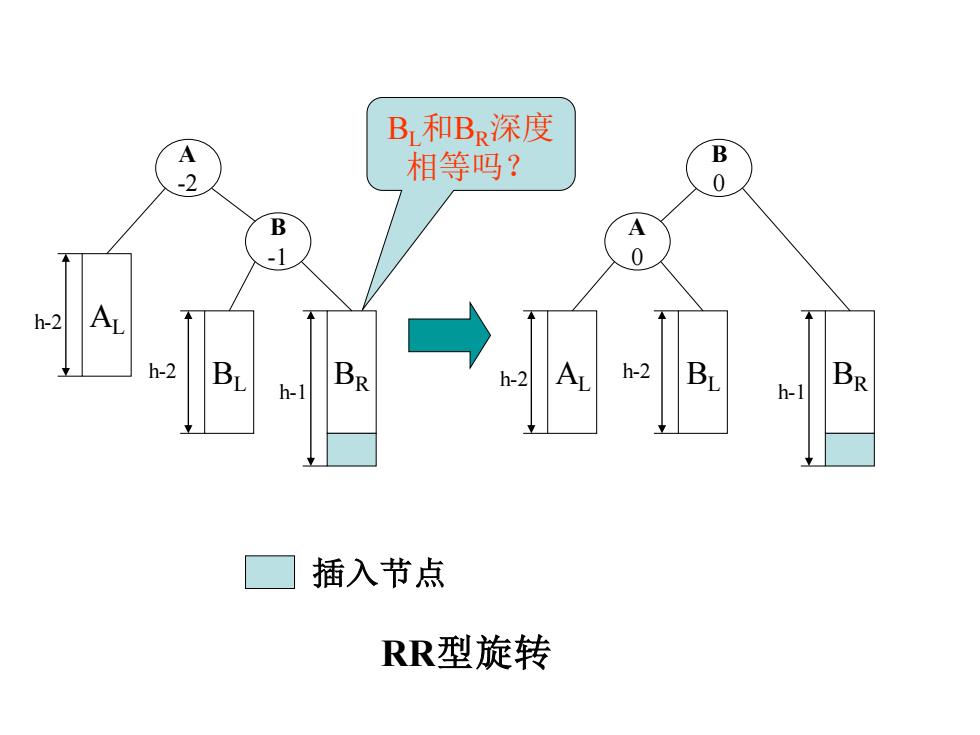
B和BR深度 A 相等吗? B 0 B A -1 0 h-2 A h-2 B h-2 h-2 h-1 BR AL B h-】 BR 插入节点 RR型旋转
A -2 B -1 h-2 AL BL BR h-1 h-2 B 0 A 0 BL h-2 BR h-1 h-2 AL 插入节点 RR型旋转 BL和BR深度 相等吗?