
·24 智能系统学报 第13卷 分别扮演着不同角色,形成的科学宇宙观是不确定 命题泛逻辑理论框架,其结构是一个四维空间 论。因为人们根本不可能在了解整个时空内的全部 [0,1],空间的中心点0代表有界逻辑(其中包含刚 信息的状态下去认识世界、解决问题,所以不确定 性逻辑x,y,z∈{0,1)。从O点伸出的4个坐标轴 性永远无法回避,形成的科学方法论只能是演化 h,k,B,e∈0,1分别代表4种不同类型的命题级不确 论,它必须适应涌现效应和生态平衡的需要,其理 定性。各种可能存在的命题级柔性逻辑都是四维空 论基础必然发生根本性改变。这是智能信息处理中 间[0,1]中连续分布的一个点,使用者可根据需要处 必须面对和解决的新问题。 理的不确定性及其不确定程度值来选择相应的柔性 假设3必须严格区分两类不同性质的矛盾 命题逻辑使用。 与确定性推理排斥一切矛盾不同,在不确定性 下面简单介绍相对于这个研究目标已经具备了 推理中必须严格区分逻辑矛盾和辩证矛盾,它们是 哪些研究基础。 两类不同性质的矛盾。逻辑矛盾是在任何一个逻辑 3.2布尔信息处理的有关情况 系统中都不允许出现的判定性错误,必须予以排 I)基于逻辑推理法的布尔信息处理 除。如在二值逻辑中判定命题A是真同时又是假, 英国数学家G.Boole1854年在《思维规律》 在连续值逻辑中判定命题B的真度是0.7,同时又是 中提出布尔逻辑算子组,它为标准逻辑(刚性逻 0.3,这些都是不允许出现的逻辑矛盾。辩证矛盾是 辑)奠定了理论基础2,可满足布尔信息处理的全 不确定性推理的研究对象,无处不在,必须正面研 部需要。图4给出了布尔逻辑算子组在概率论中的 究。如在二值逻辑中判定钱币同时具有正面和反 集合意义:设对象域U中有两个集合A和B,当任意 面,是一个对立统一体,这个辩证矛盾不能排除。 事件u出现在集合A中时,命题x(u∈A)的真值是1, 如果判定命题A(钱币正面向上)是真,同时又判定是 否则是0;当任意事件u出现在集合B中时,命题 假(钱币反面向上),这就是必须排除的逻辑矛盾。 y(u∈B)的真值是1,否则是0。基于这个集合含义, 而在连续值逻辑中,判定命题B的真度是0.7,就意 可以证明布尔逻辑算子组是完全正确的。 味着已经判定B的假度是0.3,这种真假同时存在于 命题真度之中的情况,就是一种辩证矛盾(不确定 0 性),千万不能排斥。 2.8小结 智能信息处理要面对现实世界中可能存在的各 AVB x-y1101 种确定性和不确定性,其右极限是:现实中可能存 (a)逻辑算子的集合含义 b)逻辑算子的 真值表 在的所有不确定性全部包含在待解决的问题中,只 有最完整的柔性逻辑才能描述和求解。而传统数学 图4布尔逻辑算子组及其在概率论中的集合意义 Fig.4 Boolean logic operator group and its set meaning in 中的形式演绎是智能信息处理的左极限:它通过抽 probability theory 象或忽略,可把现实中所有的不确定性全部理想化 2)基于神经网络信息变换法的布尔信息处理 为确定性,允许用刚性逻辑描述和求解。一般智能 1943年心理学家McCulloch和数学家W 信息处理介于两个极限之间,其中部分因素是确定 Pitts提出二值神经元信息变换模型M-P(又称感 的,部分因素是不确定的(见图3)。 知机)21。图5是二值神经元的基本结构,其中 刚性逻辑 柔性逻辑 完整的柔性逻辑 x,y,z∈(0,1,a、b是输人权系数,e是反应阈值,v=ar+ 左极限 一般情况 右极限 by-e是整合函数,经T[v进行0、1限幅处理后输出 全部因素具 部分因素具 全部因素具 乙,结果只有0或1状态,每一次信息处理都有△t的延迟。 有确定性 有不确定性 有不确定性 细胞壁 0,1限制器 图3智能信息处理对逻辑学的需求 整和黑 输出 Fig.3 The need for intelligent information processing to ax+by-e logic I(v] 3命题泛逻辑的研究目标和研究基础 延迟△1 什△出 图5二值神经元MP模型的基本结构 3.1命题泛逻辑的研究目标 Fig.5 The basic structure of the two value neuron M-P 如前所述,命题泛逻辑的研究目标是建立一个 model
分别扮演着不同角色,形成的科学宇宙观是不确定 论。因为人们根本不可能在了解整个时空内的全部 信息的状态下去认识世界、解决问题,所以不确定 性永远无法回避,形成的科学方法论只能是演化 论,它必须适应涌现效应和生态平衡的需要,其理 论基础必然发生根本性改变。这是智能信息处理中 必须面对和解决的新问题。 假设 3 必须严格区分两类不同性质的矛盾 A B A B B 与确定性推理排斥一切矛盾不同,在不确定性 推理中必须严格区分逻辑矛盾和辩证矛盾,它们是 两类不同性质的矛盾。逻辑矛盾是在任何一个逻辑 系统中都不允许出现的判定性错误,必须予以排 除。如在二值逻辑中判定命题 是真同时又是假, 在连续值逻辑中判定命题 的真度是 0.7,同时又是 0.3,这些都是不允许出现的逻辑矛盾。辩证矛盾是 不确定性推理的研究对象,无处不在,必须正面研 究。如在二值逻辑中判定钱币同时具有正面和反 面,是一个对立统一体,这个辩证矛盾不能排除。 如果判定命题 (钱币正面向上) 是真,同时又判定是 假 (钱币反面向上),这就是必须排除的逻辑矛盾。 而在连续值逻辑中,判定命题 的真度是 0.7,就意 味着已经判定 的假度是 0.3,这种真假同时存在于 命题真度之中的情况,就是一种辩证矛盾 (不确定 性),千万不能排斥。 2.8 小结 智能信息处理要面对现实世界中可能存在的各 种确定性和不确定性,其右极限是:现实中可能存 在的所有不确定性全部包含在待解决的问题中,只 有最完整的柔性逻辑才能描述和求解。而传统数学 中的形式演绎是智能信息处理的左极限:它通过抽 象或忽略,可把现实中所有的不确定性全部理想化 为确定性,允许用刚性逻辑描述和求解。一般智能 信息处理介于两个极限之间,其中部分因素是确定 的,部分因素是不确定的 (见图 3)。 ݆ᕓ䕧䒽 ᴀᕓ䕧䒽 Ⴘ᪠⮰ᴀᕓ䕧䒽 ጒᲭ䭼 ڣ䘔ఌ㉌ڔ ᰵᕓ ̬㝘ᗱۡ 䘔ܲఌ㉌ڣ ᰵ̹ᕓ टᲭ䭼 ڣ䘔ఌ㉌ڔ ᰵ̹ᕓ 图 3 智能信息处理对逻辑学的需求 Fig. 3 The need for intelligent information processing to logic 3 命题泛逻辑的研究目标和研究基础 3.1 命题泛逻辑的研究目标 如前所述,命题泛逻辑的研究目标是建立一个 [0,1] 4 O x, y,z ∈ {0,1} O h, k, β, e ∈ [0,1] [0,1] 4 命题泛逻辑理论框架,其结构是一个四维空间 ,空间的中心点 代表有界逻辑 (其中包含刚 性逻辑 )。从 点伸出的 4 个坐标轴 分别代表 4 种不同类型的命题级不确 定性。各种可能存在的命题级柔性逻辑都是四维空 间 中连续分布的一个点,使用者可根据需要处 理的不确定性及其不确定程度值来选择相应的柔性 命题逻辑使用。 下面简单介绍相对于这个研究目标已经具备了 哪些研究基础。 3.2 布尔信息处理的有关情况 1) 基于逻辑推理法的布尔信息处理 U A B u A x (u ∈ A) u B y (u ∈ B) 英国数学家 G. Boole 1854 年在《思维规律》 中提出布尔逻辑算子组,它为标准逻辑 (刚性逻 辑) 奠定了理论基础[22] ,可满足布尔信息处理的全 部需要。图 4 给出了布尔逻辑算子组在概率论中的 集合意义:设对象域 中有两个集合 和 ,当任意 事件 出现在集合 中时,命题 的真值是 1, 否则是 0;当任意事件 出现在集合 中时,命题 的真值是 1,否则是 0。基于这个集合含义, 可以证明布尔逻辑算子组是完全正确的。 A A A A A A B A B U U U U A A A A U B B B B A B 1C(u) 0 u y(u)=cB(u) x(u)=cA(u) y x x y x y x y x 1 1 1 1 11 1 111 11 10 0 0 0 0 0 0 0 00 0 (a) 䕧䒽ッၼ⮰䯲ऴॗ͵ (b) 䕧䒽ッၼ⮰ ⱋը㶔 图 4 布尔逻辑算子组及其在概率论中的集合意义 Fig. 4 Boolean logic operator group and its set meaning in probability theory 2) 基于神经网络信息变换法的布尔信息处理 M−P x, y,z ∈ {0,1} a、b e v = ax+ by−e Γ[v] z ∆t 1943 年心理学家 McCulloch 和数学家 W. Pitts 提出二值神经元信息变换模型 (又称感 知机) [ 2 3 ]。图 5 是二值神经元的基本结构,其中 , 是输入权系数, 是反应阈值, 是整合函数,经 进行 0、1 限幅处理后输出 ,结果只有 0 或 1 状态,每一次信息处理都有 的延迟。 x y z v ax+by−e ax bx b a 1 0 t e −e 䒿ڑ 䬴ը ᪠সஔ 䒿ܦ ㏲㘊෭ 0, 1䭼ݢஔ ᱯ ը ᐢ䔋 ∆t t+∆t Γ[v] 图 5 二值神经元 M-P 模型的基本结构 Fig. 5 The basic structure of the two value neuron M-P model ·24· 智 能 系 统 学 报 第 13 卷
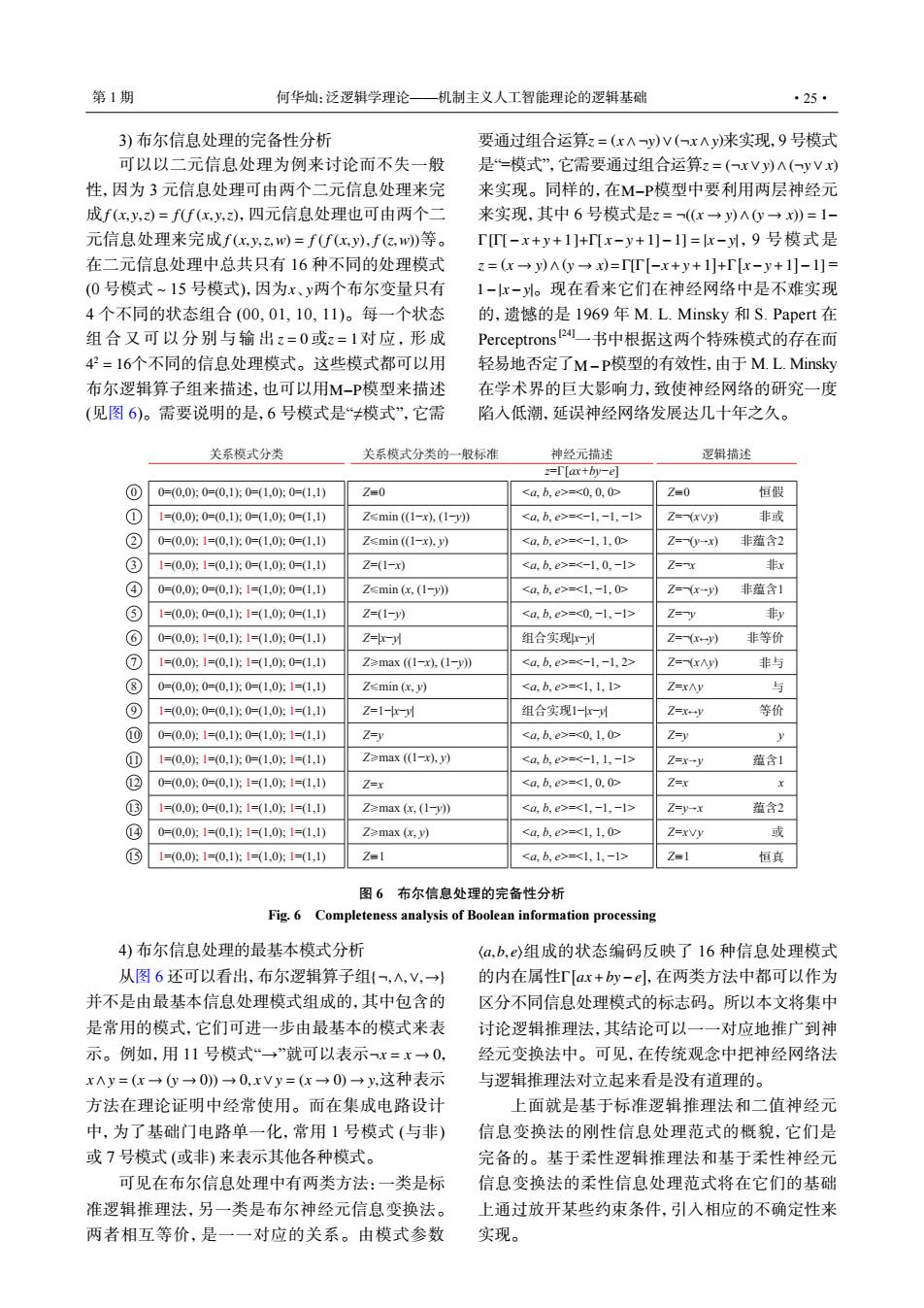
第1期 何华灿:泛逻辑学理论一机制主义人工智能理论的逻辑基础 ·25· 3)布尔信息处理的完备性分析 要通过组合运算z=(xAy)V(xAy)来实现,9号模式 可以以二元信息处理为例来讨论而不失一般 是“=模式”,它需要通过组合运算z=(xVy)A(yVx) 性,因为3元信息处理可由两个二元信息处理来完 来实现。同样的,在M-P模型中要利用两层神经元 成f(x,y,)=ff(x,y,,四元信息处理也可由两个二 来实现,其中6号模式是z=(x→y)A0y→x)=1- 元信息处理来完成f(x,y,乙,w)=ff(xy,f(亿,w)等。 「[-x+y+1]+T[x-y+1]-1)=x-y,9号模式是 在二元信息处理中总共只有16种不同的处理模式 z=(x→y)A(y→x)=T[-x+y+1]+T[x-y+1]-1]= (0号模式~15号模式),因为x、y两个布尔变量只有 1-x-。现在看来它们在神经网络中是不难实现 4个不同的状态组合(00,01,10,11)。每一个状态 的,遗憾的是1969年M.L.Minsky和S.Papert在 组合又可以分别与输出z=0或?=1对应,形成 Perceptrons叫一书中根据这两个特殊模式的存在而 42=16个不同的信息处理模式。这些模式都可以用 轻易地否定了M-p模型的有效性,由于M.L.Minsky 布尔逻辑算子组来描述,也可以用M-P模型来描述 在学术界的巨大影响力,致使神经网络的研究一度 (见图6)。需要说明的是,6号模式是“≠模式”,它需 陷入低潮,延误神经网络发展达几十年之久。 关系模式分类 关系模式分类的一般标准 神经元描述 逻辑描述 z=T[ax+by-e) 0=(0,0:0=(0,1方0=(1,0:0=(1,1) Z=0 <a,b.e>=<0.0,0> Z=0 恒假 ⊙ 1=(0.0):0=(0.1)50=(1,0):0=(1,1) Zsmin ((1-x),(1-v)) <a,b,e>=<-1-1,-1> Z=-(xvy) 非或 ② 0=0,0:1=0,1):0=(1,0):0=(1,1) Zsmin ((1-x),y) <a.b,e>=<-1,1,0> Z=-0-x) 非蕴含2 ③ 1=(0,0:1=(0,1):0=(1,0):0=(1,1) Z=(1-x <a,b,e>=<-1,0,-1 Z=-x 非x ④ 0=(0,0):0=(0,1):1=(1,0):0=(1,1) Z≤min(x,(1-y) <a,b,e>=<l,-1,0> Z=-(x-y) 非蕴含1 ⑤ 1=(0,0:0=(0,1)51=(1,0):0=(1,1) Z=(1-y) <ab,e>=<0,-1,-12 Z=-y 非y ⑥ 0=(0,0):1=0,1):1=(1,0):0=(1,1) Z=- 组合实现一川 Z=-x-y) 非等价 ① 1=(0,0):1=(0,1):1=(1,0:0=(1,1) Z≥max(1-x),(1-y) <a,b,e>=<-1,-1,2> Z=-(xAy) 非与 ⑧ 0=(0,0):0=(0,1)50=(1,0);1=(1,1) Z≤min(x,y) <a,b,e>=<1,1,1> Z=xAy 与 ⑨ 1=(0,0:0=(0,150=(1,0):1=(1,1) Z=1--y 组合实现1--川 Z=x-y 等价 ⑩ 0=(0,0:1=(0,1):0=(1,0:1=(1,1) Z=y <a,b,e>=<0,1,0> Z=y y ① 1=0,0):1=(0,1):0=(1,0):1=(1,1) Z≥max(1-x),y) <a,b,e>=<-l,1,-1> Z=x-y 蕴含1 @ 0=(0,0):0=0,1):1=(1,0):1=(1,1) Z=x <a,b,e>=<1,0,0 Z=x x ③ 1=(0,0):0=(0,1):1=(1,0):1=(1,1) Z≥maxx,(1-y) <a,b,e>=<1,-1,-1> Z=y-x 蕴含2 ©④ 0=(0,0):1=(0,1):1=(1,0);1=(1,1) Z≥max(x,y) <a,b,e>=<l,1,0> Z=rvy 或 1=(0,0):1=(0,1):1=(1,0):1=(1,1) Z=1 <a,b,e>=<1,1,-1> Z=1 恒其 图6布尔信息处理的完备性分析 Fig.6 Completeness analysis of Boolean information processing 4)布尔信息处理的最基本模式分析 (a,b,e)组成的状态编码反映了16种信息处理模式 从图6还可以看出,布尔逻辑算子组(一,Λ,V,→} 的内在属性Γ[ar+by-e,在两类方法中都可以作为 并不是由最基本信息处理模式组成的,其中包含的 区分不同信息处理模式的标志码。所以本文将集中 是常用的模式,它们可进一步由最基本的模式来表 讨论逻辑推理法,其结论可以一一对应地推广到神 示。例如,用11号模式“→”就可以表示x=x→0, 经元变换法中。可见,在传统观念中把神经网络法 xAy=(x→y→0)→0,xVy=(x→0)→y,这种表示 与逻辑推理法对立起来看是没有道理的。 方法在理论证明中经常使用。而在集成电路设计 上面就是基于标准逻辑推理法和二值神经元 中,为了基础门电路单一化,常用1号模式(与非) 信息变换法的刚性信息处理范式的概貌,它们是 或7号模式(或非)来表示其他各种模式。 完备的。基于柔性逻辑推理法和基于柔性神经元 可见在布尔信息处理中有两类方法:一类是标 信息变换法的柔性信息处理范式将在它们的基础 准逻辑推理法,另一类是布尔神经元信息变换法。 上通过放开某些约束条件,引入相应的不确定性来 两者相互等价,是一一对应的关系。由模式参数 实现
3) 布尔信息处理的完备性分析 f (x, y,z) = f(f (x, y,z) f (x, y,z,w) = f (f (x, y), f (z,w)) x y z = 0 z = 1 4 2 = 16 M−P 可以以二元信息处理为例来讨论而不失一般 性,因为 3 元信息处理可由两个二元信息处理来完 成 ,四元信息处理也可由两个二 元信息处理来完成 等。 在二元信息处理中总共只有 16 种不同的处理模式 (0 号模式~15 号模式),因为 、 两个布尔变量只有 4 个不同的状态组合 (00, 01, 10, 11)。每一个状态 组合又可以分别与输出 或 对应,形成 个不同的信息处理模式。这些模式都可以用 布尔逻辑算子组来描述,也可以用 模型来描述 (见图 6)。需要说明的是,6 号模式是“≠模式”,它需 z = (x∧ ¬y)∨(¬x∧y) z = (¬x∨y)∧(¬y∨ x) M−P z = ¬((x → y)∧(y → x)) = 1− Γ[Γ[− x+y+1]+Γ[ x−y+1]−1] = |x−y| z = (x → y)∧(y → x)=Γ[Γ [ −x+y+1 ] +Γ[ x−y+1 ] −1] 1−|x−y| M−P 要通过组合运算 来实现,9 号模式 是“=模式”,它需要通过组合运算 来实现。同样的,在 模型中要利用两层神经元 来实现,其中 6 号模式是 ,9 号模式是 = 。现在看来它们在神经网络中是不难实现 的,遗憾的是 1969 年 M. L. Minsky 和 S. Papert 在 Perceptrons[24]一书中根据这两个特殊模式的存在而 轻易地否定了 模型的有效性,由于 M. L. Minsky 在学术界的巨大影响力,致使神经网络的研究一度 陷入低潮,延误神经网络发展达几十年之久。 ڟ㈧Ὅᐻܲㆧ ڟ㈧Ὅᐻܲㆧ⮰̬㝘ᴳ۲ ⺊㏻ٯ䔜 䕧䒽䔜 z=Γ[ax+by−e] 0 0=(0,0); 0=(0,1); 0=(1,0); 0=(1,1) Zį0 <a, b, e>=<0, 0, 0> Zį0 ᕾճ 2 0=(0,0); 1=(0,1); 0=(1,0); 0=(1,1) Zİmin ((1−x), y) <a, b, e>=<−1, 1, 0> Z=¬(yėx) 䲊㪠ॗ2 3 1=(0,0); 1=(0,1); 0=(1,0); 0=(1,1) Z=(1−x) <a, b, e>=<−1, 0, −1> Z=¬x 䲊x 4 0=(0,0); 0=(0,1); 1=(1,0); 0=(1,1) Zİmin (x, (1−y)) <a, b, e>=<1, −1, 0> Z=¬(xėy) 䲊㪠ॗ1 5 1=(0,0); 0=(0,1); 1=(1,0); 0=(1,1) Z=(1−y) <a, b, e>=<0, −1, −1> Z=¬y 䲊y 6 0=(0,0); 1=(0,1); 1=(1,0); 0=(1,1) Z=|x−y| ㏰ऴ⣜|x−y| Z=¬(x↔y) 䲊ふУ 7 1=(0,0); 1=(0,1); 1=(1,0); 0=(1,1) Zımax ((1−x), (1−y)) <a, b, e>=<−1, −1, 2> Z=¬(xġy) 䲊̺ 9 1=(0,0); 0=(0,1); 0=(1,0); 1=(1,1) Z=1−|x−y| ㏰ऴ⣜1−|x−y| Z=x↔y ふУ 10 0=(0,0); 1=(0,1); 0=(1,0); 1=(1,1) Z=y <a, b, e>=<0, 1, 0> Z=y y 11 1=(0,0); 1=(0,1); 0=(1,0); 1=(1,1) Zımax ((1−x), y) <a, b, e>=<−1, 1, −1> Z=xėy 㪠ॗ1 12 0=(0,0); 0=(0,1); 1=(1,0); 1=(1,1) Z=x <a, b, e>=<1, 0, 0> Z=x x 13 1=(0,0); 0=(0,1); 1=(1,0); 1=(1,1) Zımax (x, (1−y)) <a, b, e>=<1, −1, −1> Z=yėx 㪠ॗ2 0=(0,0); 1=(0,1); 1=(1,0); 1=(1,1) Zımax (x, y) <a, b, e>=<1, 1, 0> Z=xĢy ᝂ 15 1=(0,0); 1=(0,1); 1=(1,0); 1=(1,1) Zį1 <a, b, e>=<1, 1, −1> Zį1 ᕾⱋ 14 1 1=(0,0); 0=(0,1); 0=(1,0); 0=(1,1) Zİmin ((1−x), (1−y)) <a, b, e>=<−1, −1, −1> Z=¬(xĢy) 䲊ᝂ 8 0=(0,0); 0=(0,1); 0=(1,0); 1=(1,1) Zİmin (x, y) <a, b, e>=<1, 1, 1> Z=xġy ̺ 图 6 布尔信息处理的完备性分析 Fig. 6 Completeness analysis of Boolean information processing 4) 布尔信息处理的最基本模式分析 {¬,∧,∨,→} ¬x = x → 0 x∧y = (x → (y → 0)) → 0, x∨y = (x → 0) → y, 从图 6 还可以看出,布尔逻辑算子组 并不是由最基本信息处理模式组成的,其中包含的 是常用的模式,它们可进一步由最基本的模式来表 示。例如,用 11 号模式“→”就可以表示 , 这种表示 方法在理论证明中经常使用。而在集成电路设计 中,为了基础门电路单一化,常用 1 号模式 (与非) 或 7 号模式 (或非) 来表示其他各种模式。 可见在布尔信息处理中有两类方法:一类是标 准逻辑推理法,另一类是布尔神经元信息变换法。 两者相互等价,是一一对应的关系。由模式参数 ⟨a,b, e⟩ Γ [ ax+by−e ] 组成的状态编码反映了 16 种信息处理模式 的内在属性 ,在两类方法中都可以作为 区分不同信息处理模式的标志码。所以本文将集中 讨论逻辑推理法,其结论可以一一对应地推广到神 经元变换法中。可见,在传统观念中把神经网络法 与逻辑推理法对立起来看是没有道理的。 上面就是基于标准逻辑推理法和二值神经元 信息变换法的刚性信息处理范式的概貌,它们是 完备的。基于柔性逻辑推理法和基于柔性神经元 信息变换法的柔性信息处理范式将在它们的基础 上通过放开某些约束条件,引入相应的不确定性来 实现。 第 1 期 何华灿:泛逻辑学理论——机制主义人工智能理论的逻辑基础 ·25·