
2013-3-1 Review:Mechanical Concepts of Energy v2 Kinetic energy KE=m2 (kJ) Potential energy PE =mg (kJ) Total energy of a system v2 E=U+KE+PE-U+m+ (kJ) Energy of a system per unit mass e=u+ke+pe-u+2 (kJ/kg) 2-13 Units for Energy Units for kinetic energy,potential energy and work are the same and they are: SI:N-m=Jor kJ (Joule) English:foot-pound force ft-lbfor British Thermal Unit,BTU 2-14 7
2013-3-1 7 Review: Mechanical Concepts of Energy 2-13 Total energy of a system Energy of a system per unit mass Potential energy Kinetic energy Units for kinetic energy, potential energy and work are the same and they are: SI: N·m = J or kJ (Joule) English: foot-pound force ft·lbf or British Thermal Unit, BTU Units for Energy 2-14

2013-3-1 0 Total Energy 2-15 Summary:Energy of a System In summary,the change in energy of a system from state 1 to state 2 is E2-E,=(U2-U)+(KE2-KE)+(PE2-PE) △E=△U+△KE+△PE Since an arbitrary value E can be assigned to the energy of a system at a given state 1,no particular significance can be attached to the value of energy at state 1 or any other state.Only changes in the energy of a system between states have significance. 2-16 8
2013-3-1 8 Total Energy 2-15 http://bcs.wiley.com/he-bcs/Books?action=index&itemId=0470918012&bcsId=6606 Summary: Energy of a System 2-16 ►In summary, the change in energy of a system from state 1 to state 2 is E2 – E1 = (U2 – U1) + (KE2 – KE1) + (PE2 – PE1) ΔE = ΔU + ΔKE + ΔPE ►Since an arbitrary value E1 can be assigned to the energy of a system at a given state 1, no particular significance can be attached to the value of energy at state 1 or any other state. Only changes in the energy of a system between states have significance

2013-3-1 Energy Transfer by Work Heat System boundary Energy can be transferred to and from closed systems CLOSED by two means only: SYSTEM Work Work (m=constant) Heat You've most probably studied work in mechanics. However,thermodynamics deals with phenomena not included within the scope of mechanics,and this requires a broader interpretation of work. 2-17 Heat vs.Work >Both are recognized at the boundaries of a 8g8tenaneycostnebounares6ouincen Systems possess energy,but not heat or work. >Both are associated with a process,not a state Unlike properties,heat or work has no meaning at a state. Both are path functions(i.e..their magnitudes depend on the path followed during a process as well as the end states). >Both are directional quantities:have magnitude AND direction 9
2013-3-1 9 Energy Transfer by Work & Heat ►Energy can be transferred to and from closed systems by two means only: ►Work ►Heat ►You’ve most probably studied work in mechanics. However, thermodynamics deals with phenomena not included within the scope of mechanics, and this requires a broader interpretation of work. 2-17 Heat vs. Work ¾ Both are recognized at the boundaries of a system as they cross the boundaries (boundary phenomena) ¾ Systems possess energy, but not heat or work. ¾ Both are associated with a process, not a state. ¾ Unlike properties, heat or work has no meaning at a state. ¾ Both are path functions (i.e., their magnitudes depend on the path followed during a process as well as the end states). ¾ Both are directional quantities: have magnitude AND direction

2013-3-1 Heat vs.Work Properties are point functions/have exact differentials(d). (2 V=-V=△V J Path functions(Heat and work)have inexact differentials(8) 2m 2 Properties are point functions; 8W=W12 (not△W) but heat and work are path functions(their magnitudes depend on the path followed). 2.19 Illustrations of Work When a spring is compressed, energy is transferred to the spring by work. When a gas in a closed vessel is stirred,energy is transferred to the gas by work. When a battery is charged electrically,energy is transferred to the battery contents by work. The first two examples of work are encompassed by mechanics.The third example is an example of the broader interpretation of work encountered in thermodynamics. 2-20 10
2013-3-1 10 Heat vs. Work 2-19 Properties are point functions; but heat and work are path functions (their magnitudes depend on the path followed). Properties are point functions / have exact differentials (d ). Path functions (Heat and work) have inexact differentials (δ ) ►When a spring is compressed, energy is transferred to the spring by work. ►When a gas in a closed vessel is stirred, energy is transferred to the gas by work. ►When a battery is charged electrically, energy is transferred to the battery contents by work. Illustrations of Work ►The first two examples of work are encompassed by mechanics. The third example is an example of the broader interpretation of work encountered in thermodynamics. 2-20
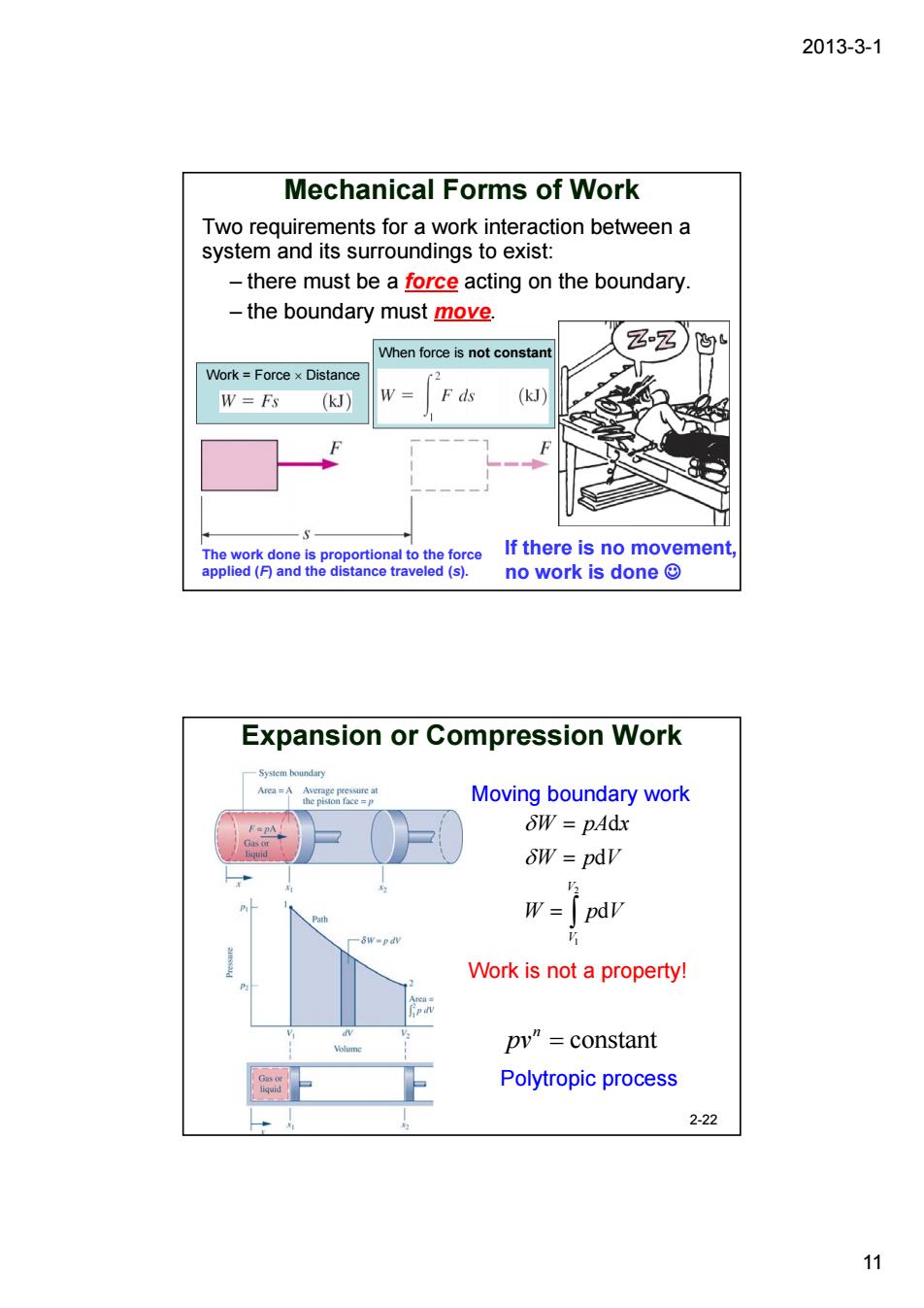
2013-3-1 Mechanical Forms of Work Two requirements for a work interaction between a system and its surroundings to exist: -there must be a force acting on the boundary -the boundary must move. zz) When force is not constar Nork=Forcex Distanc W=F() (kJ If there is no movement no work is done© Expansion or Compression Work A月 Moving boundary work SW=pAdx SW =pdv W=「pdV Work is not a property! pv"=constant Polytropic process 2-22 11
2013-3-1 11 Mechanical Forms of Work Two requirements for a work interaction between a system and its surroundings to exist: – there must be a force acting on the boundary. – the boundary must move. The work done is proportional to the force applied (F) and the distance traveled (s). Work = Force × Distance When force is not constant If there is no movement, no work is done ☺ Expansion or Compression Work 2-22 2 1 d d d V V W pA x W pV W pV δ δ = = = ∫ constant n pv = Work is not a property! Moving boundary work Polytropic process