
Clauses for Abstract 0-CFA (2) (Cp)(if to then tf else) iff (C,可)=t∧ (C,)=tA(C,)=t好N c(1)CC()∧C(2)≤C() (C,)=(topt经) iff (C,)=经A(C,)=t经 PPA Section 3.1 C F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 16
Clauses for Abstract 0-CFA (2) ( bC, ρb) |= (if t `0 0 then t `1 1 else t `2 2 ) ` iff ( bC, ρb) |= t `0 0 ∧ ( bC, ρb) |= t `1 1 ∧ ( bC, ρb) |= t `2 2 ∧ bC(`1) ⊆ bC(`) ∧ bC(`2) ⊆ bC(`) ( bC, ρb) |= (t `1 1 op t `2 2 ) ` iff ( bC, ρb) |= t `1 1 ∧ ( bC, ρb) |= t `2 2 PPA Section 3.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 16

Clauses for Abstract 0-CFA (3) (C,p)(>)e iff (fnC() (c,)=(t经t经) iff (C,)=t1A(C,)=tA ((nr>t始8)∈c(1): (c,可上t始o c(2)(x)ΛC(o)cC() PPA Section 3.1 F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 17
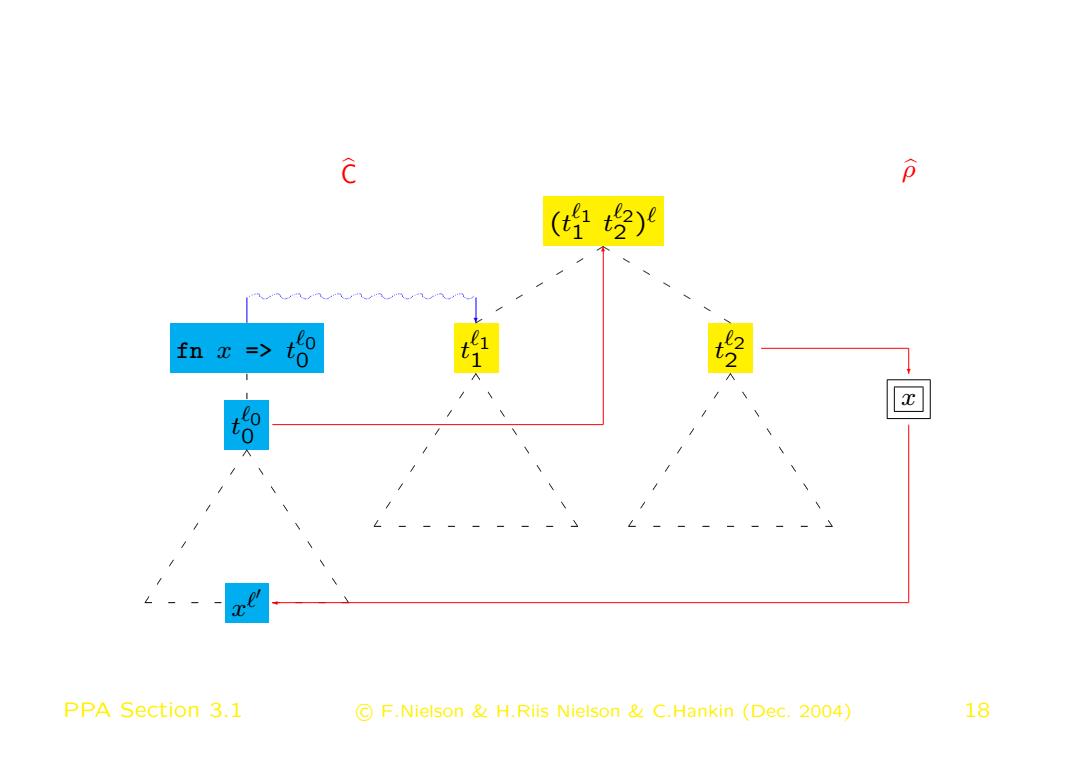
Clauses for Abstract 0-CFA (3) ( bC, ρb) |= (fn x => t `0 0 ) ` iff {fn x => t `0 0 } ⊆ bC(`) ( bC, ρb) |= (t `1 1 t `2 2 ) ` iff ( bC, ρb) |= t `1 1 ∧ ( bC, ρb) |= t `2 2 ∧ (∀( fn x => t `0 0 ) ∈ bC(`1) : ( bC, ρb) |= t `0 0 ∧ bC(`2) ⊆ ρb(x) ∧ bC(`0) ⊆ bC(`)) PPA Section 3.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 17
c p (t好)‘ fn x = 7八 PPA Section 3.1 C F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 18
bC ρb (t `1 1 t `2 2 ) ` t `1 1 t `2 2 fn x => t `0 0 t `0 0 x x ` 0 ✛ ✻ ❄ ❄ PPA Section 3.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 18

Clauses for Abstract 0-CFA (4) (C,p)(fun f x=>eo)e iff {fun f x=>eo}C(e) (C,)上(tt经) iff(C,)=t经A(C,)=tN ((nx>8)∈c(e1): (c,)=t始0 C(2)p()C(o)c())A ((un f a=>t始)∈C(1):(C,p)片t始8A C(2)p()C(o)C(e)A {fun f x=>top(f)) PPA Section 3.1 C F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 19
Clauses for Abstract 0-CFA (4) ( bC, ρb) |= (fun f x => e0) ` iff {fun f x => e0} ⊆ bC(`) ( bC, ρb) |= (t `1 1 t `2 2 ) ` iff ( bC, ρb) |= t `1 1 ∧ ( bC, ρb) |= t `2 2 ∧ (∀( fn x => t `0 0 ) ∈ bC(`1) : ( bC, ρb) |= t `0 0 ∧ bC(`2) ⊆ ρb(x) ∧ bC(`0) ⊆ bC(`)) ∧ (∀( fun f x => t `0 0 ) ∈ bC(`1) : ( bC, ρb) |= t `0 0 ∧ bC(`2) ⊆ ρb(x) ∧ bC(`0) ⊆ bC(`) ∧ {fun f x => t `0 0 } ⊆ ρb(f) ) PPA Section 3.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 19

Example: Two guesses for ((fn x=>x1)2 (fn y=>y3)4)5 (Ce;pe) (Ce,pe) 1 {fn y =y3} (fn y =>y 2 {fn x = x2} fn x = x1} 3 0 0 4 {fn y ->y3 (fn y=>y3) 5 {fn y => y3) {fn y =>y3 (fn y -y3) 0 y 0 0 Checking the guesses: (Ce,pe)=(fnx=>x21)2(fny=>y3)4)5 (C,)≠(tnx=>x21)2(fny=>y3)4)5 PPA Section 3.1 F.Nielson H.Riis Nielson C.Hankin (Dec.2004) 20
Example: Two guesses for ((fn x => x1) 2 (fn y => y3) 4) 5 ( bCe, ρbe) ( bC 0 e , ρb 0 e ) 1 2 3 4 5 x y {fn y => y3} {fn x => x1} ∅ {fn y => y3} {fn y => y3} {fn y => y3} ∅ {fn y => y3} {fn x => x1} ∅ {fn y => y3} {fn y => y3} ∅ ∅ Checking the guesses: ( bCe, ρbe) |= ((fn x => x1) 2 (fn y => y3) 4) 5 ( bC 0 e , ρb 0 e ) 6|= ((fn x => x1) 2 (fn y => y3) 4) 5 PPA Section 3.1 c F.Nielson & H.Riis Nielson & C.Hankin (Dec. 2004) 20