二、有限域GF()上的椭圆曲线 (二)E,(a,b)上的点在Abel群上加法规则的几何意义 ③ (不同点相加)横坐标不同的两个点P,Q相加时,先在它们之间 画一条直线并求直线与曲线的第三个交点R,则P+Q+R=O,即 P+Q=-R. 1 P+Q之值 P+Q+R=0
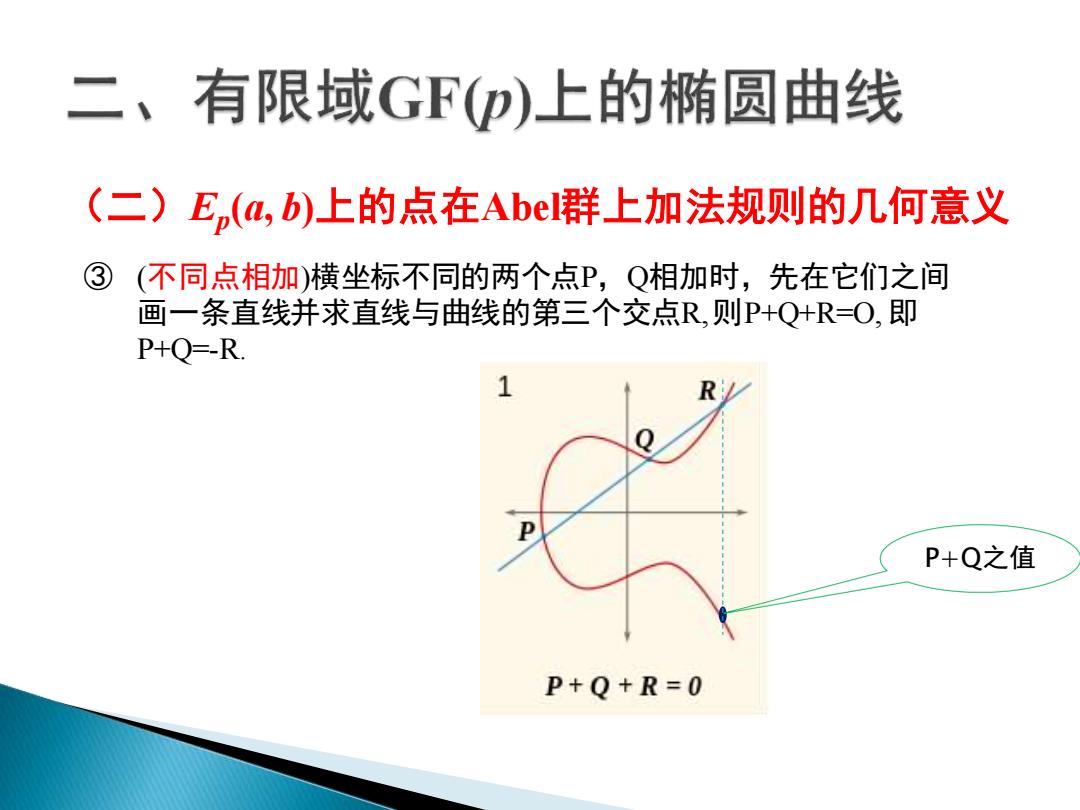
(二)Ep (a, b)上的点在Abel群上加法规则的几何意义 ③ (不同点相加)横坐标不同的两个点P,Q相加时,先在它们之间 画一条直线并求直线与曲线的第三个交点R, 则P+Q+R=O, 即 P+Q=-R. P+Q之值
二、有限域GF()上的椭圆曲线 (二)E,(a,b)上的点在Abe群上加法规则的几何意义 ④ (相同点相加)两个相同的点Q相加时,通过该点画一条切线, 切线与曲线交于另一个点P,则Q+Q=2Q=-P. 2 2Q之值 P+Q+Q=0
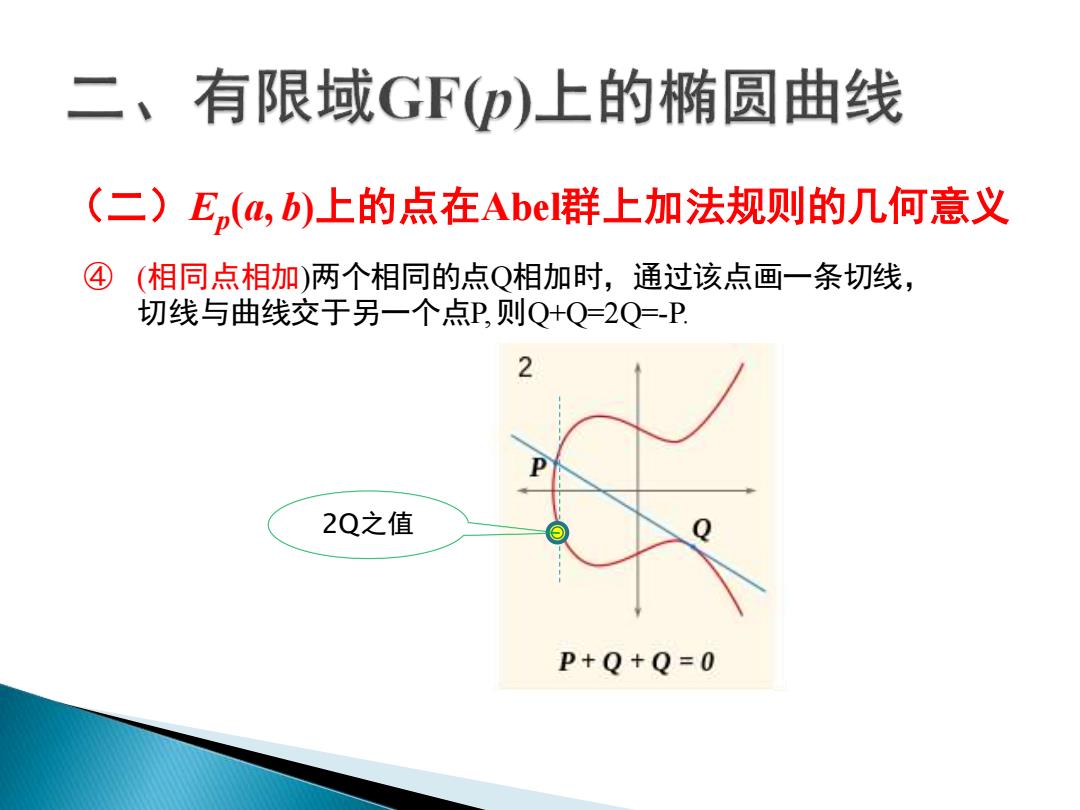
(二)Ep (a, b)上的点在Abel群上加法规则的几何意义 ④ (相同点相加)两个相同的点Q相加时,通过该点画一条切线, 切线与曲线交于另一个点P, 则Q+Q=2Q=-P. 2Q之值

二、有限域GF(p)上的椭圆曲线 (三)椭圆曲线点乘规则 P=P+P+..+P(k个P相加) ②s,t为整数,(S+t)P=sP+P s(P)=(st)P 定义1椭圆曲线的阶:椭圆曲线E,(a,b)在有限域GF(p)所有离 散点的个数,记为N,称为椭圆曲线的阶。 定义2点的阶:P=(K,y)∈E,(a,b),若存在最小的整数n,使得 nP=O,则称n为椭圆曲线上点P的阶。 定义3生成元:除了无穷远点O之外,椭圆曲线上任何可以 生成所有点的点都可称为椭圆曲线E的生成元,但并不是所 有点都是生成元
(三)椭圆曲线点乘规则 ① kP=P+P+…+P (k个P相加) ② s, t为整数,(s+t)P=sP+tP, s(tP)=(st)P 定义1椭圆曲线的阶:椭圆曲线Ep (a, b)在有限域GF(p)所有离 散点的个数,记为N,称为椭圆曲线的阶。 定义2点的阶:P=(x,y)∈Ep (a, b), 若存在最小的整数n,使得 nP=O, 则称n为椭圆曲线上点P的阶。 定义3生成元:除了无穷远点O之外,椭圆曲线上任何可以 生成所有点的点都可称为椭圆曲线E的生成元,但并不是所 有点都是生成元

三、椭圆曲线上点的计算 1 Hasse's theorem on elliptic curves Hasse's theorem on elliptic curves,also referred to as the Hasse bound,provides an estimate of the number of points on an elliptic curve over a finite field,bounding the value below. If N is the number of points on the elliptic curve E over a finite field with p elements,then Helmut Hasse's result states that lW-(p+1≤2VP
1、Hasse's theorem on elliptic curves Hasse's theorem on elliptic curves, also referred to as the Hasse bound, provides an estimate of the number of points on an elliptic curve over a finite field, bounding the value below. If N is the number of points on the elliptic curve E over a finite field with p elements, then Helmut Hasse's result states that N − ( p +1) 2 p