校绵鼎 Example p2 t2 pl tl p4 ● t3 p3
Example p2 t1 p1 t2 p4 t3 p3

效绵鼎 Definition of Petri Net C=(P,T,LO) Places P={p1,P2,P3,,Pn} Transitions T={t1,t2,t3,…,tn} 0 Input I:T>Pr(r=number of places) ot Output O:T→Pq(q=number of places)t· .12
Definition of Petri Net ◼ C = ( P, T, I, O) Places P = { p1 , p2 , p3 , …, pn} Transitions T = { t1 , t2 , t3 , …, tn} Input I : T → P r (r = number of places) •t Output O : T → P q (q = number of places) t • 12

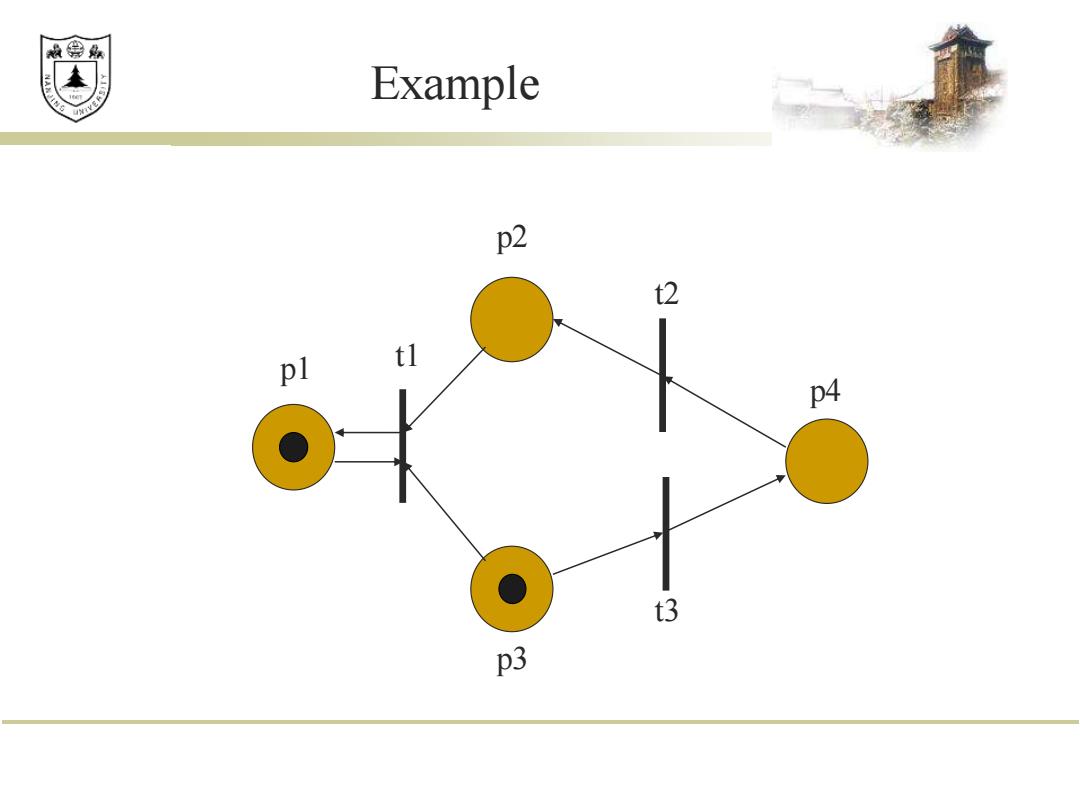
效绵鼎 marking u assignment of tokens to the places of Petri net u=μ1,u2,u3,…ln p2 t2 pl tl p4 3 13 p3
◼ marking µ : assignment of tokens to the places of Petri net µ = µ1 , µ2 , µ3 , … µn 13 p2 t1 p1 t2 p4 t3 p3

效绵 Applications performance evaluation communication protocols distributed-software systems distributed-database systems concurrent and parallel programs ◆ industrial control systems discrete-events systems multiprocessor memory systems dataflow-computing systems fault-tolerant systems etc,etc,etc
Applications ◼ performance evaluation ◼ communication protocols ◼ distributed-software systems ◼ distributed-database systems ◼ concurrent and parallel programs ◼ industrial control systems ◼ discrete-events systems ◼ multiprocessor memory systems ◼ dataflow-computing systems ◼ fault-tolerant systems ◼ etc, etc, etc

效绵 Basics of Petri Nets Petri net consist two types of nodes:places and transitions.And arc exists only from a place to a transition or from a transition to a place. A place may have zero or more tokens. Graphically,places,transitions,arcs,and tokens are represented respectively by:circles,bars,arrows, and dots. Below is an example Petri net with two places and one transaction. P2 15
Basics of Petri Nets ◼ Petri net consist two types of nodes: places and transitions. And arc exists only from a place to a transition or from a transition to a place. ◼ A place may have zero or more tokens. ◼ Graphically, places, transitions, arcs, and tokens are represented respectively by: circles, bars, arrows, and dots. ◼ Below is an example Petri net with two places and one transaction. p 15 p1 2 t1