
解:(1)采用集总参数法,根据题意有: pev +hF(t-ty)=g,V dt dr 对应的初始条件: T=0,t=tf d8, hF 令B=t-t,方程可以化为: 8= dt pc hF 分离变量积分的解为:B=cexp(- peV )+9P hF 由初始条件,得:c=-g业 故=g-ep hF hF hF ] (2)采用集总参数法,对电熨斗底板做能量守恒分析有:+ er是+-ro,F-)=g T=0.t=if 12
12

3.3对流边界条件下一维瞬态导热 第三类边界条件下大平壁、长圆柱及球体的加热 或冷却是工程上常见的一维非稳态导热问题。 3.3.1无限大平壁对称冷却或加热问题的分析解 假设:厚度为2δ,导热系数2、 热扩散率a为常数,无内热源 初始温度与两侧流体相同,为1o。 =0 两侧流体温度突然降低为1:,并 保持不变,平壁表面与流体间对 流换热表面传热系数为常数。 考虑温度场的对称性,选取 te 坐标系如图,仅需讨论半个平壁 的导热问题。 -6 0 这是一维的非稳态导热问题, 13
13 3.3 对流边界条件下一维瞬态导热 第三类边界条件下大平壁、长圆柱及球体的加热 或冷却是工程上常见的一维非稳态导热问题。 3.3.1 无限大平壁对称冷却或加热问题的分析解 假设:厚度为2,导热系数、 热扩散率为常数,无内热源, 初始温度与两侧流体相同,为t0。 两侧流体温度突然降低为t f,并 保持不变,平壁表面与流体间对 流换热表面传热系数h为常数。 考虑温度场的对称性,选取 坐标系如图,仅需讨论半个平壁 的导热问题。 这是一维的非稳态导热问题。 t f t f

1.数学模型 0t 821 令0=t-t 20 =a =a Ox2 过余温度 ar x=0, t= x=0,0=0=1-t 00 x=0, =0(对称性) x=0, =0 8x x=δ,-见=h(t-) x=δ, 采用分离变量法求解:取 0=X(x)·φ(T) 只为的函数 1 do 1 d'x 只为心的函数 ag dr x dx I do 1 d2x 只能为常数: aΦdx 14
14 1. 数学模型 2 2 t t a x = 0, 0 = =t t 0, 0 t x x = = (对称性) , ( f ) t x h t t x = − = − 2 2 a x = 0, 0 0 f = = = − t t x 0, 0 x = = x h , x = − = f 令 = −t t 过余温度 采用分离变量法求解:取 = X (x) ( ) 2 2 1 1 d x d X d X d a = 只为 的函数 只为 x 的函数 = = 2 2 1 1 dx d X d X d 只能为常数: a

1 d 1 d2X u ag dr X dx2 =u 积分得: p=Cer→ceas 1 d2x X dx2 =-g2x=c:cos(ox)+c,sin(x) 0(x,t)=[Acos(ax)+Bsin (sx)e 由对称边界条件得:B=0 0(x,t)=Acos(x)e 由对流换热边界条件得:-Aesin(eδeas:=hAcos()ea: 化简得: =cot(6)=cotu Bi 15
15 = = 2 2 1 1 dx d X d X d a 积分得: 2 1 1 a a c e c e − = X c ( x) c ( x) dx d X X cos sin 1 2 3 2 2 2 = − = + ( ) ( ) ( ) 2 , cos sin a x A x B x e − = + 由对称边界条件得: ( ) ( ) 2 0 , cos a B x A x e − = = 由对流换热边界条件得: ( ( ) ) ( ) 2 2 sin cos a a A e hA e − − − − = 化简得: ( ) ( ) cot = cot = cot = = h h Bi
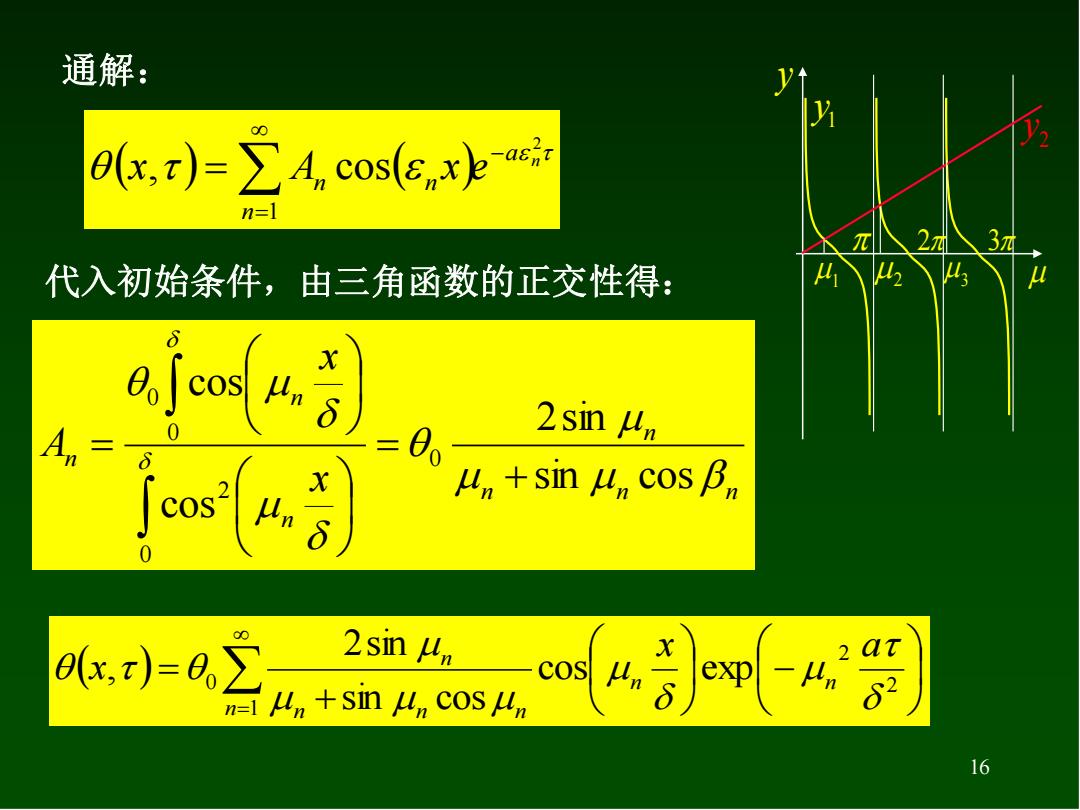
通解: (x)=>4 cos(xe-aei n= 2 3 代入初始条件,由三角函数的正交性得: 442 43 An 二00 2smn u ò u+sin u cos B 0x)=0∑ 2sin un w+sin L cOS i =l coe-gg) 16
16 1 2 3 1 y y 2 y 2 3 ( ) ( ) 2 1 , cos a n n n n x A x e − = = 通解: 代入初始条件,由三角函数的正交性得: n n n n n n n x x A sin cos 2sin cos cos 0 0 2 0 0 + = = ( ) = − + = 1 2 2 0 cos exp sin cos 2sin , n n n n n n n x a x