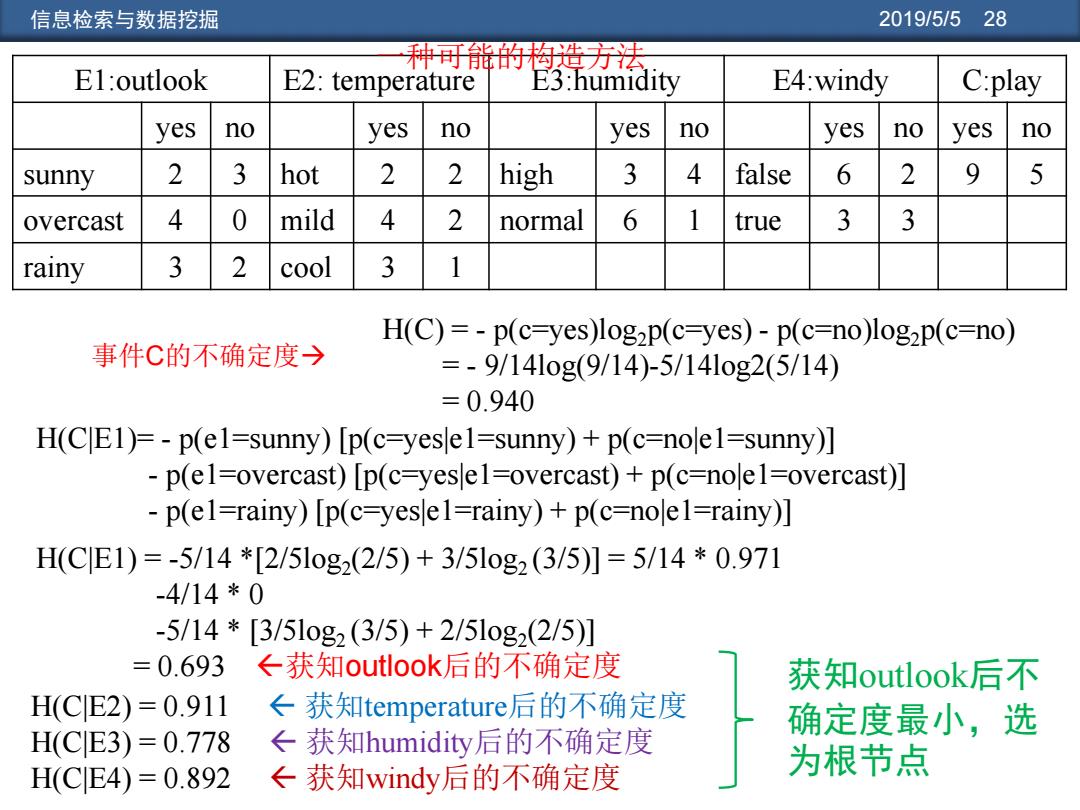
信息检索与数据挖掘 2019/5/528 种可能的构造方法 El:outlook E2:temperature E3:humidity E4:windy C:play yes no yes no yes no yes no yes no sunny 2 3 hot 2 2 high 3 4 false 6 2 9 5 overcast 4 0 mild 4 2 normal 6 1 true 3 3 rainy 3 2 cool 3 1 H(C)=-p(c=yes)log2p(c-yes)-p(c=no)log2p(c=no) 事件C的不确定度→ =-9/141og(9/14)-5/141og2(5/14) =0.940 H(CE1)=-p(el=sunny)[p(c=yesle1=sunny)+p(c=nole1=sunny)] p(el=overcast)[p(c-yeslel=overcast)+p(c=nole1=overcast)] p(el=rainy)[p(c-yesel=rainy)+p(c=nolel=rainy)] H(CE1)=-5/14*[2/51og2(2/5)+3/51og2(3/5)】=5/14*0.971 -4/14*0 -5/14*[3/51og2(3/5)+2/51og2(2/5)] =0.693 ←获知outlook后的不确定度 获知outlook后不 H(CE2)=0.911 ←获知temperature后的不确定度 确定度最小,选 H(CE3)=0.778 ←获知humidity后的不确定度 H(CE4)=0.892 ←获知windy后的不确定度 为根节点
信息检索与数据挖掘 2019/5/5 28 E1:outlook E2: temperature E3:humidity E4:windy C:play yes no yes no yes no yes no yes no sunny 2 3 hot 2 2 high 3 4 false 6 2 9 5 overcast 4 0 mild 4 2 normal 6 1 true 3 3 rainy 3 2 cool 3 1 H(C|E1)= - p(e1=sunny) [p(c=yes|e1=sunny) + p(c=no|e1=sunny)] - p(e1=overcast) [p(c=yes|e1=overcast) + p(c=no|e1=overcast)] - p(e1=rainy) [p(c=yes|e1=rainy) + p(c=no|e1=rainy)] H(C|E1) = -5/14 *[2/5log2 (2/5) + 3/5log2 (3/5)] = 5/14 * 0.971 -4/14 * 0 -5/14 * [3/5log2 (3/5) + 2/5log2 (2/5)] = 0.693 获知outlook后的不确定度 H(C|E2) = 0.911 获知temperature后的不确定度 H(C|E3) = 0.778 获知humidity后的不确定度 H(C|E4) = 0.892 获知windy后的不确定度 H(C) = - p(c=yes)log2p(c=yes) - p(c=no)log2p(c=no) = - 9/14log(9/14)-5/14log2(5/14) = 0.940 事件C的不确定度 获知outlook后不 确定度最小,选 为根节点 一种可能的构造方法
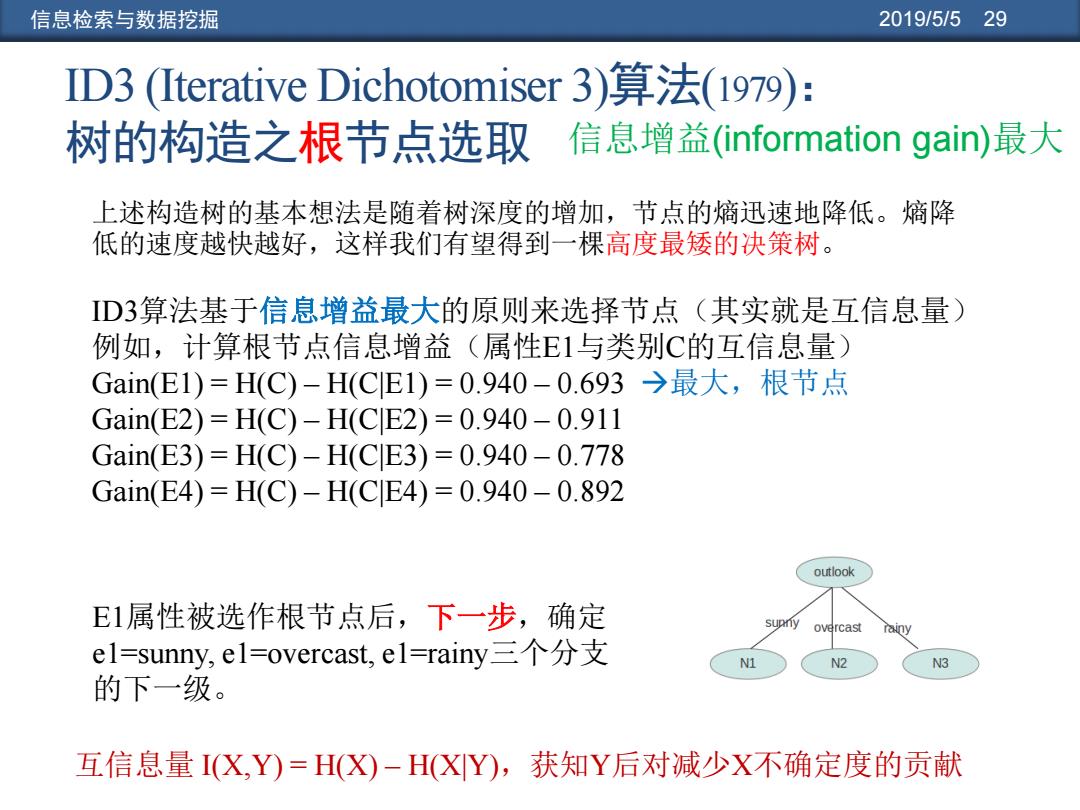
信息检索与数据挖掘 2019/5/529 ID3(Iterative Dichotomiser3)算法(1979): 树的构造之根节点选取 ,信息增益(information gain)最大 上述构造树的基本想法是随着树深度的增加,节点的熵迅速地降低。熵降 低的速度越快越好,这样我们有望得到一棵高度最矮的决策树。 ID3算法基于信息增益最大的原则来选择节点(其实就是互信息量) 例如,计算根节点信息增益(属性E1与类别C的互信息量) Gain(E1)=H(C)-H(CE1)=0.940-0.693→最大,根节点 Gain(E2)=H(C)-H(CE2)=0.940-0.911 Gain(E3)=H(C)-H(CE3)=0.940-0.778 Gain(E4)=H(C)-H(CE4)=0.940-0.892 outlook E1属性被选作根节点后,下一步,确定 overcast el=sunny,el=overcast,.el=rainy三个分支 N1 N2 N3 的下一级。 互信息量I(X,Y)=H(X)-H(XY),获知Y后对减少X不确定度的贡献
信息检索与数据挖掘 2019/5/5 29 ID3算法基于信息增益最大的原则来选择节点(其实就是互信息量) 例如,计算根节点信息增益(属性E1与类别C的互信息量) Gain(E1) = H(C) – H(C|E1) = 0.940 – 0.693 最大,根节点 Gain(E2) = H(C) – H(C|E2) = 0.940 – 0.911 Gain(E3) = H(C) – H(C|E3) = 0.940 – 0.778 Gain(E4) = H(C) – H(C|E4) = 0.940 – 0.892 E1属性被选作根节点后,下一步,确定 e1=sunny, e1=overcast, e1=rainy三个分支 的下一级。 ID3 (Iterative Dichotomiser 3)算法(1979): 树的构造之根节点选取 上述构造树的基本想法是随着树深度的增加,节点的熵迅速地降低。熵降 低的速度越快越好,这样我们有望得到一棵高度最矮的决策树。 互信息量 I(X,Y) = H(X) – H(X|Y),获知Y后对减少X不确定度的贡献 信息增益(information gain)最大
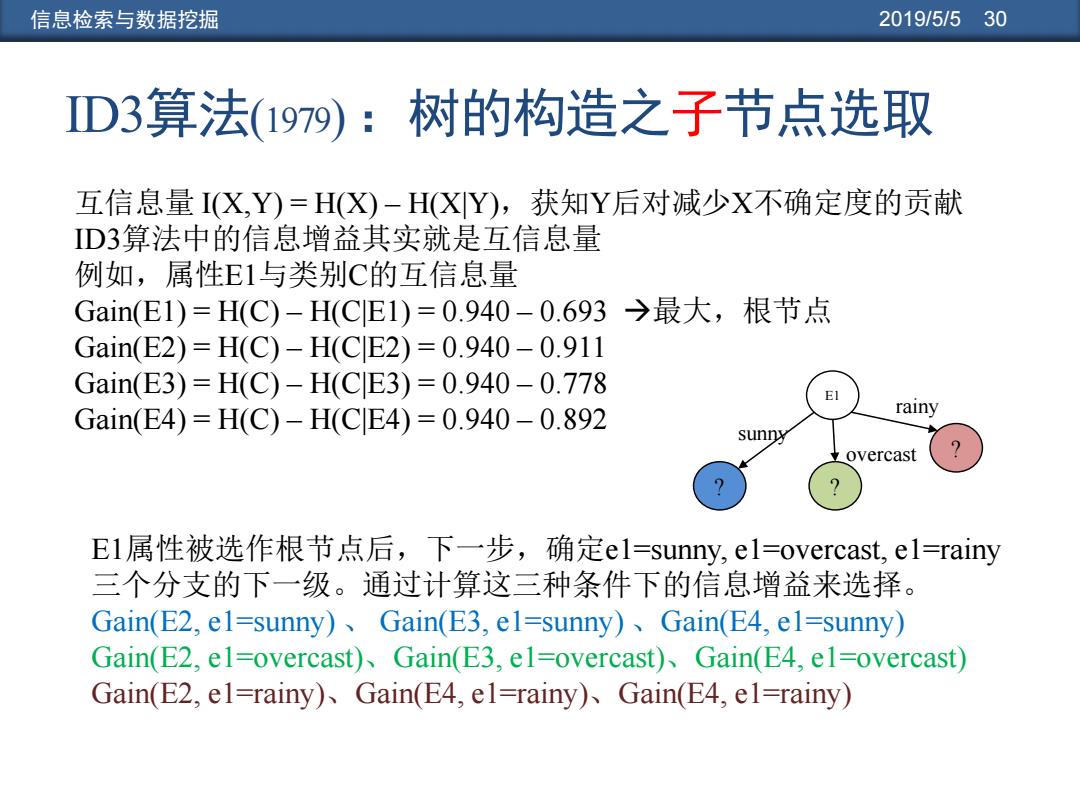
信息检索与数据挖掘 2019/5/530 D3算法(1979):树的构造之子节点选取 互信息量I(X,Y)=H(X)-H(XY),获知Y后对减少X不确定度的贡献 ID3算法中的信息增益其实就是互信息量 例如,属性E1与类别C的互信息量 Gain(E1)=H(C)-H(CE1)=0.940-0.693→最大,根节点 Gain(E2)=H(C)-H(CE2)=0.940-0.911 Gain(E3)=H(C)-H(CE3)=0.940-0.778 El Gain(E4)=H(C)-H(CE4)=0.940-0.892 rainy sunny 立overcast El属性被选作根节点后,下一步,确定el=sunny,el=overcast,el=rainy 三个分支的下一级。通过计算这三种条件下的信息增益来选择。 Gain(E2,el-sunny)、Gain(E3,el=sunny)、Gain(E4,el=sunny) Gain(E2,el=overcast)Gain(E3,el=overcast)Gain(E4,el=overcast) Gain(E2,el=rainy)Gain(E4,el=rainy)Gain(E4,el=rainy)
信息检索与数据挖掘 2019/5/5 30 互信息量 I(X,Y) = H(X) – H(X|Y),获知Y后对减少X不确定度的贡献 ID3算法中的信息增益其实就是互信息量 例如,属性E1与类别C的互信息量 Gain(E1) = H(C) – H(C|E1) = 0.940 – 0.693 最大,根节点 Gain(E2) = H(C) – H(C|E2) = 0.940 – 0.911 Gain(E3) = H(C) – H(C|E3) = 0.940 – 0.778 Gain(E4) = H(C) – H(C|E4) = 0.940 – 0.892 E1属性被选作根节点后,下一步,确定e1=sunny, e1=overcast, e1=rainy 三个分支的下一级。通过计算这三种条件下的信息增益来选择。 Gain(E2, e1=sunny) 、 Gain(E3, e1=sunny) 、Gain(E4, e1=sunny) Gain(E2, e1=overcast)、Gain(E3, e1=overcast)、Gain(E4, e1=overcast) Gain(E2, e1=rainy)、Gain(E4, e1=rainy)、Gain(E4, e1=rainy) ID3算法(1979) :树的构造之子节点选取 E1 ? ? ? sunny overcast rainy
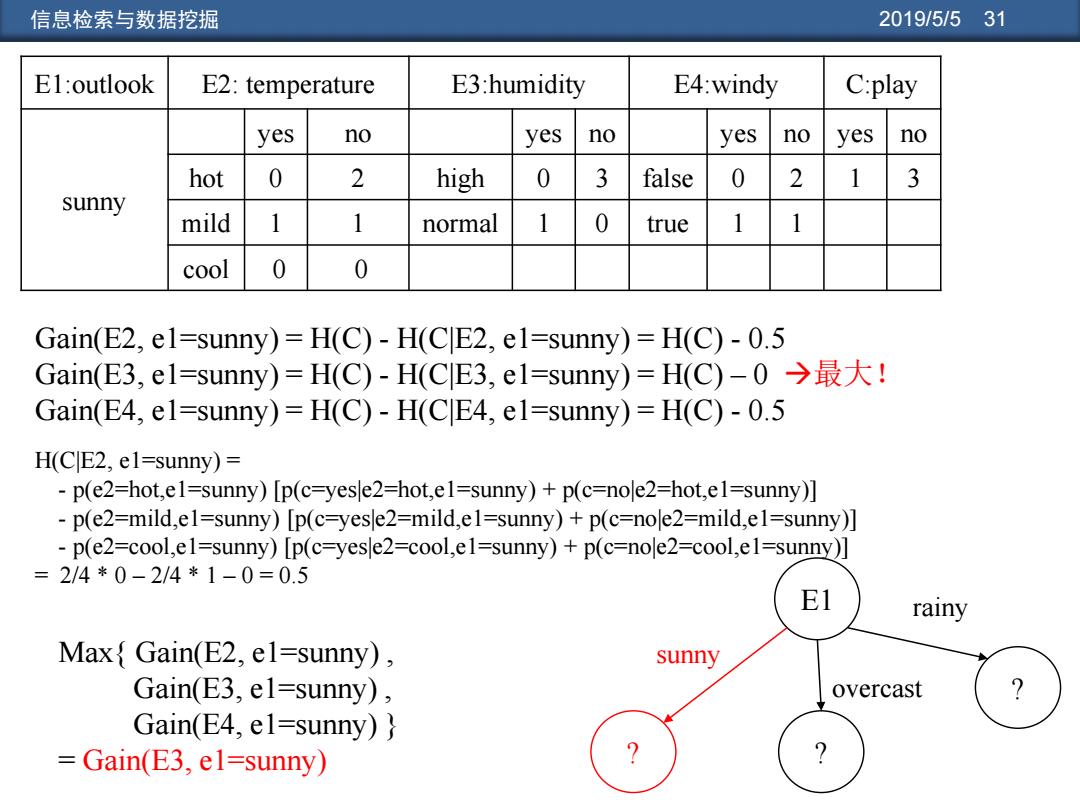
信息检索与数据挖掘 2019/5/531 El:outlook E2:temperature E3:humidity E4:windy C:play yes no yes no yes no yes no hot 0 2 high 0 3 false 0 2 1 3 sunny mild 1 1 normal 1 0 true 1 1 cool 0 0 Gain(E2,el=sunny)=H(C)-H(CE2,e1=sunny)=H(C)-0.5 Gain(E3,el=sunny)=H(C)-H(ClE3,el=sunny)=H(C)-0→最大! Gain(E4,el=sunny)=H(C)-H(CE4,el=sunny)=H(C)-0.5 H(CE2,el=sunny)= -p(e2=hot,e1=sunny)[p(c=yesle2=hot,e1=sunny)+p(c=nole2=hot,e1=sunny)] p(e2=mild,el=sunny)[p(c=yesle2=mild,e1=sunny)+p(c=nole2=mild,el=sunny)] -p(e2=cool,e1=sunny)[p(c=yesle2=cool,e1=sunny)+p(c=nole2=cool,e1=sunny)] =2/4*0-2/4*1-0=0.5 E1 rainy Max{Gain(E2,el=sunny), sunny Gain(E3,el=sunny), overcast ? Gain(E4,el=sunny)} Gain(E3,el=sunny) ? ?
信息检索与数据挖掘 2019/5/5 31 E1:outlook E2: temperature E3:humidity E4:windy C:play sunny yes no yes no yes no yes no hot 0 2 high 0 3 false 0 2 1 3 mild 1 1 normal 1 0 true 1 1 cool 0 0 E1 ? ? ? sunny overcast rainy Gain(E2, e1=sunny) = H(C) - H(C|E2, e1=sunny) = H(C) - 0.5 Gain(E3, e1=sunny) = H(C) - H(C|E3, e1=sunny) = H(C) – 0 最大! Gain(E4, e1=sunny) = H(C) - H(C|E4, e1=sunny) = H(C) - 0.5 H(C|E2, e1=sunny) = - p(e2=hot,e1=sunny) [p(c=yes|e2=hot,e1=sunny) + p(c=no|e2=hot,e1=sunny)] - p(e2=mild,e1=sunny) [p(c=yes|e2=mild,e1=sunny) + p(c=no|e2=mild,e1=sunny)] - p(e2=cool,e1=sunny) [p(c=yes|e2=cool,e1=sunny) + p(c=no|e2=cool,e1=sunny)] = 2/4 * 0 – 2/4 * 1 – 0 = 0.5 Max{ Gain(E2, e1=sunny) , Gain(E3, e1=sunny) , Gain(E4, e1=sunny) } = Gain(E3, e1=sunny)
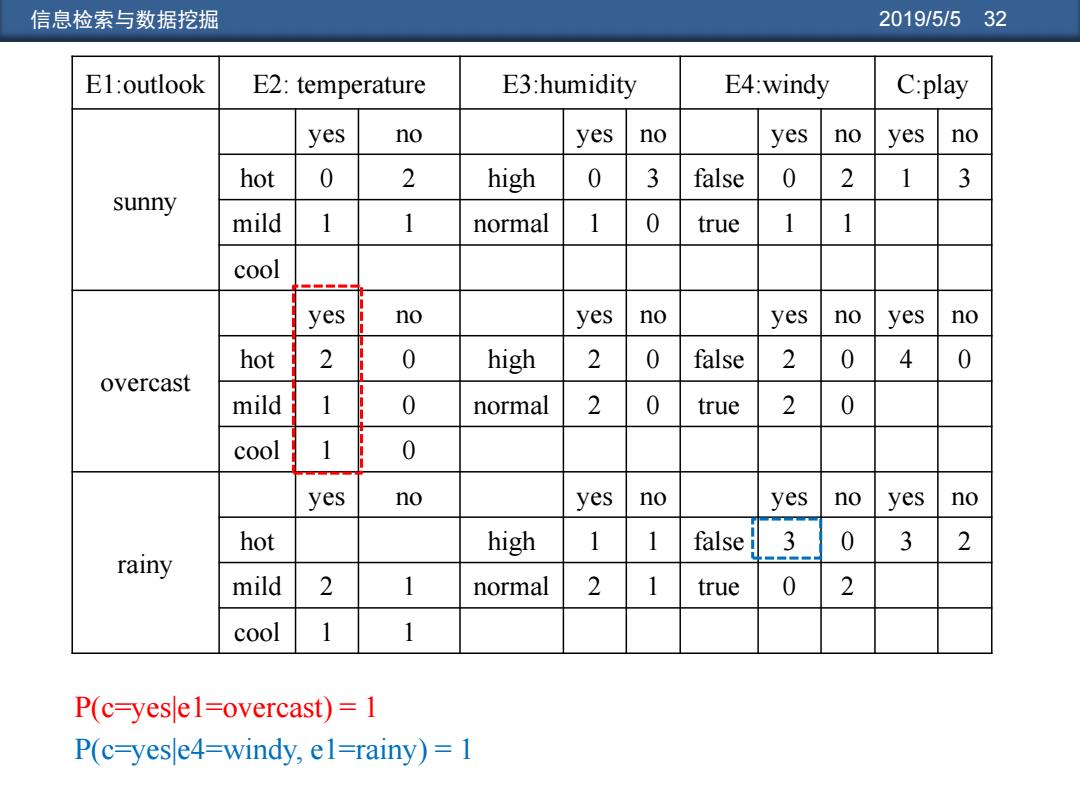
信息检索与数据挖掘 2019/5/532 El:outlook E2:temperature E3:humidity E4:windy C:play yes no yes no yes no yes no hot 0 2 high 0 3 false 0 2 1 3 sunny mild 1 1 normal 1 0 true 1 1 cool yes no yes no yes no yes no hot 2 0 high 2 0 false 2 0 4 0 overcast mild 1 0 normal 2 0 true 2 0 cool 1 0 yes no yes no yes no yes no hot high 1 1 false 3 0 3 2 rainy mild 2 normal 2 1 true 0 2 cool 1 1 P(c-yese1=overcast)=1 P(c=yese4=windy,el=rainy)=1
信息检索与数据挖掘 2019/5/5 32 E1:outlook E2: temperature E3:humidity E4:windy C:play sunny yes no yes no yes no yes no hot 0 2 high 0 3 false 0 2 1 3 mild 1 1 normal 1 0 true 1 1 cool overcast yes no yes no yes no yes no hot 2 0 high 2 0 false 2 0 4 0 mild 1 0 normal 2 0 true 2 0 cool 1 0 rainy yes no yes no yes no yes no hot high 1 1 false 3 0 3 2 mild 2 1 normal 2 1 true 0 2 cool 1 1 P(c=yes|e1=overcast) = 1 P(c=yes|e4=windy, e1=rainy) = 1