
δ=2eVn2-n2sin2i+ 2 =6(i) 明纹 6(i)=k2,k=1,2,3,. 暗纹60=(2k+1)7,k=01,2 倾角相同的光线对应同 一条干涉条纹。 上意不意道可退欢
上页 下页 返回 退出 ( ) 2 2 sin 2 2 2 e n n i i = − + = 明纹 (i) = k, k =1,2,3, 暗纹 ( ) ( ) , 0,1,2, 2 i = 2k +1 k = 倾角i相同的光线对应同 一条干涉条纹

条纹特点: 等倾条纹 ·形状: 一系列同心圆环 。条纹间隔分布:内疏外密 条纹级次分布:e一定时,k个→6个→i↓→↓ 。 膜厚变化时,条纹的移动:k一定,1个i个个 波长对条纹的影响:ke一定,个→i↓→↓ 让意下元蕴司退
上页 下页 返回 退出 • 形状: 条纹特点: 一系列同心圆环 • 条纹间隔分布: 内疏外密 • 条纹级次分布: • 波长对条纹的影响: • 膜厚变化时,条纹的移动: e 一定时, k → → i → rk 等倾条纹 k k,e 一定, i r → → k k 一定, i r → →

例题12-9用波长为2的单色光观察等倾条纹,看到视场 中心为一亮斑,外面围以若干圆环,如图所示.今若慢慢 增大薄膜的厚度,则看到的干涉圆环会有什么变化? 解:由薄膜的折射率n和折射角表示 的等倾条纹明环的条件 几 2 ne cosr+二=k2 2 知,当r=O时,级次最高,且满足: 2ne+=k入 2 这对应于中心亮斑,k是它的级次。 让无子文返回退此
上页 下页 返回 退出 例题12-9 用波长为的单色光观察等倾条纹,看到视场 中心为一亮斑,外面围以若干圆环,如图所示.今若慢慢 增大薄膜的厚度,则看到的干涉圆环会有什么变化? 解:由薄膜的折射率n和折射角r表示 的等倾条纹明环的条件 知,当 r =0时,级次最高,且满足: ne r + = k 2 2 cos c 2 2 ne k + = 这对应于中心亮斑,kc是它的级次

中 心:暗→亮→暗 e逐渐增大 中心级数:k。→k+1→k+2 中心每冒出一个亮斑(△k=1), 就意味着薄膜厚度增加A?并且 λ △e 2n 让美觉返司退
上页 下页 返回 退出 e逐渐增大 中 心:暗 亮 暗 中心级数: kc kc+1 kc+2 n e 2 = 中心每冒出一个亮斑(kc=1), 就意味着薄膜厚度增加 , e 并且
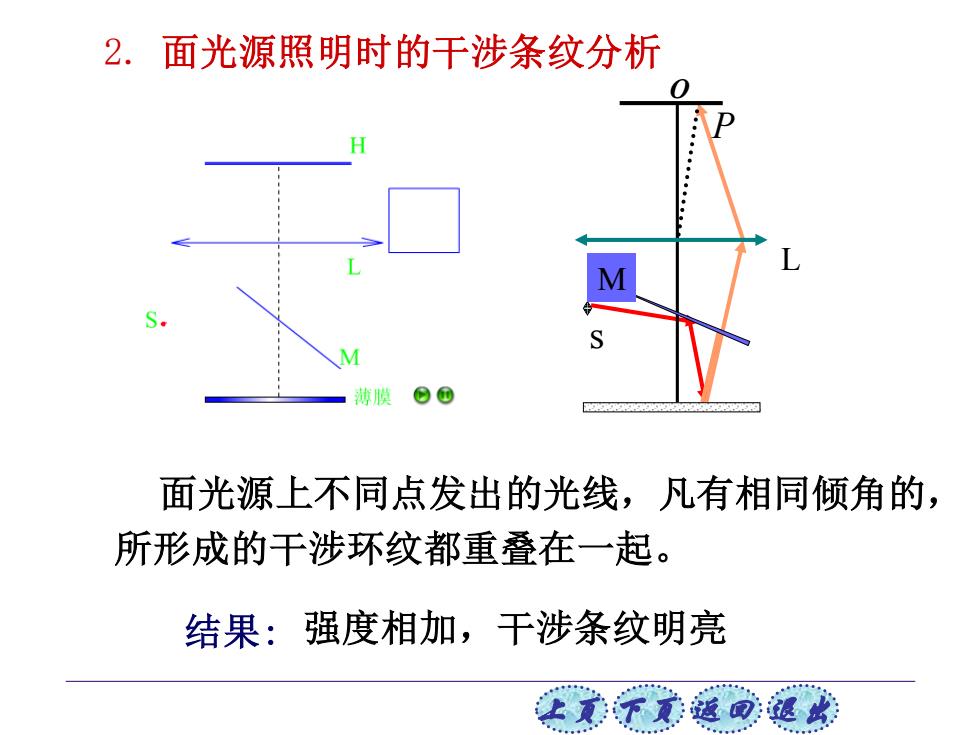
2.面光源照明时的干涉条纹分析 薄膜©© 面光源上不同点发出的光线,凡有相同倾角的, 所形成的干涉环纹都重叠在一起。 结果:强度相加,干涉条纹明亮
上页 下页 返回 退出 2. 面光源照明时的干涉条纹分析 s P O L M 面光源上不同点发出的光线,凡有相同倾角的, 所形成的干涉环纹都重叠在一起。 结果: 强度相加,干涉条纹明亮