
则E=手, 入x (a+x Are,2ra (d 1 qx 4π6(a2+x2) 当x>>a时,即在远离圆环处,有 E= 14 4π6x 相当于将带电圆环看作点电荷时的场强
则 3 2 2 2 0 1 4 ( ) x L L x E dE dl a x = = + 2 3 2 2 0 2 0 1 4 2 ( ) x q a dl a a x = + 3 2 2 2 0 1 4 ( ) qx a x = + 当x>>a时,即在远离圆环处,有 2 0 1 4 q E x = 相当于将带电圆环看作点电荷时的场强

利用上题的结果,可以求出均匀带 电圆盘轴线上的场强。将圆盘分成 无数多个同心圆环,每一圆环相当 于一个电荷元,所有圆环电荷元轴 线上的场强积分便是整个圆盘轴线上的场强。 解:将圆盘分成无穷多个圆环, 以r为半径,O为圆心、厚为dr D x的圆环,所带电量为电荷元dq? 面电荷密度。云,得 dr dg=odS而dS=2πrh 2πr -2-
利用上题的结果,可以求出均匀带 电圆盘轴线上的场强。将圆盘分成 无数多个同心圆环,每一圆环相当 于一个电荷元,所有圆环电荷元轴 线上的场强积分便是整个圆盘轴线上的场强。 q o r P x dr 解:将圆盘分成无穷多个圆环, 以r为半径,O为圆心、厚为dr 的圆环,所带电量为电荷元dq, 面电荷密度 2 ,得 q a = dr 2r dq dS = 而 dS rdr = 2 2 2 2 2 q qr dq rdr dr a a = =

利用结果E= gx 4(a+x2 式中q→dq,a>r,EdE :dB= xdq πx2+r2 ar rdr XO a
利用结果 3 2 2 2 0 1 4 ( ) qx E a x = + 式中q→dq,a→r,E→dE 3 2 2 2 0 1 4 ( ) xdq dE x r = + 3 0 2 2 2 0 1 2 4 ( ) a x r E dE dr x r = = + 2 2 3 3 0 0 2 2 2 2 2 2 0 0 1 ( ) 2 2 2 ( ) ( ) x rdr x d x r a a x r x r + = = + + 1 2 2 2 0 1 1 ( )( ) 2 2 3 0 1 2 x a x r − = + − +

Ja+ 2 -+ 注:小m+ xm-1 +C 总之,要把握信计算电荷连续分布的带 电体场强的思想: I求出电荷元dg的场强dE一一微分过程 (关键)。 【积分(叠加)求出所有电荷元的总场 强一一积分过程,即数学运算
2 2 0 1 1 ( ) 2 x a x x = − − + 2 2 2 2 2 0 0 (1 ) (1 ) 2 2 x x q x a x a x a = − = − + + 注: 1 1 1 m m x dx x C m − = + + 总之,要把握信计算电荷连续分布的带 电体场强的思想: I 求出电荷元dq的场强 --微分过程 (关键)。 II 积分(叠加)求出所有电荷元的总场 强--积分过程,即数学运算。dE
四、电力线 电通量 1、电力线密度 为形象地表示电场的 特征,了解电场的分布,在电 E。场中人为的引入一系列的曲线, 曲线各点的切线方向都与该点 场强方向一致,这样的曲线称 为电力线。通过单位面积的电力线条数称为该 dN 点的电力线密度,即然。 场强也可用电力线密 dN 度来表示:E= ds
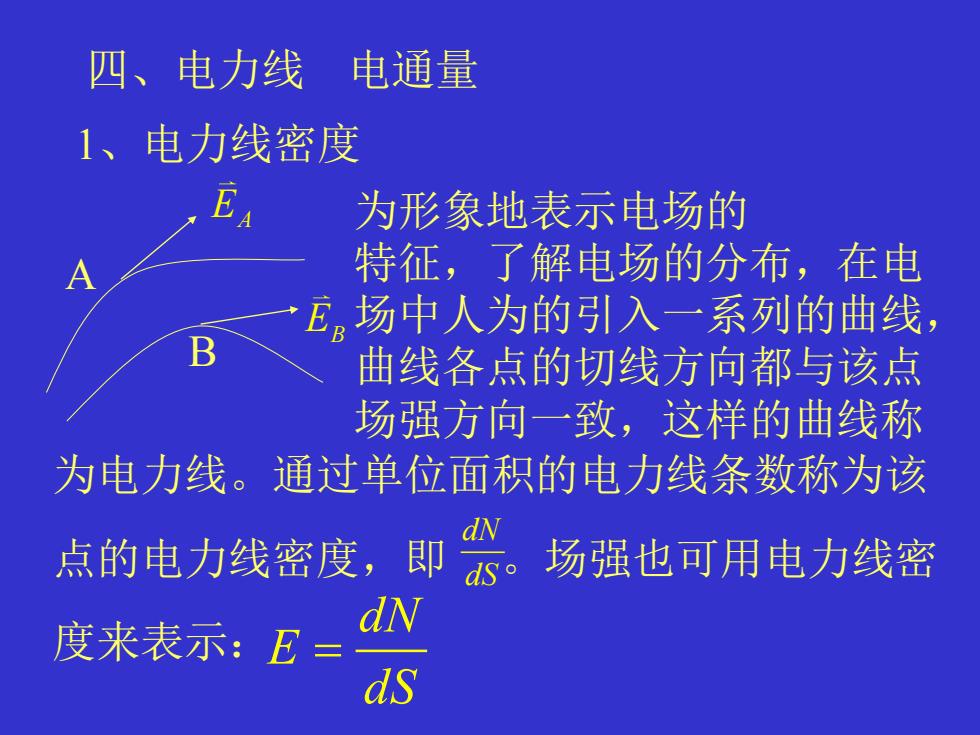
四、电力线 电通量 1、电力线密度 为形象地表示电场的 特征,了解电场的分布,在电 场中人为的引入一系列的曲线, 曲线各点的切线方向都与该点 场强方向一致,这样的曲线称 A B EA EB 为电力线。通过单位面积的电力线条数称为该 点的电力线密度,即 。场强也可用电力线密 度来表示: dN dS dN E dS =