
3.2正规文法和状态转换图 ·正规文法定义了3型语言,常见的单词可由正 规文法定义。 ●状态转换图可用于识别3型语言;它是设计和 实现扫描器的一种有效工具,是有限自动机的 直观图示
3.2 正规文法和状态转换图 •正规文法定义了3型语言,常见的单词可由正 规文法定义。 •状态转换图可用于识别3型语言;它是设计和 实现扫描器的一种有效工具,是有限自动机的 直观图示

3.2.1由正规文法构造状态转换图 ·一般说来,凡能用正规文法描 ·程序设计语言的单词都能 述的语言,均可由某种有限状 用正规文法描述; 态算法—状态转换图进行分 ·例如,标识符可定义为 析。 <标识符>→<标识符>字母 ● 状态转换图由有限个结点所 <标识符>→<标识符>数字 组成的有向图。 <标识符>→字母 ● 每个结点代表在识别分析过程 ·若把字母、数字视为终结 中扫描器所处的状态,其中含 符,则上述产生式为(左 有一个初始状态和若干个终态。 线性)正规文法 在图中,状态用圆圈表示,终 。 态用双层圆圈表示。 若我们用d表示0-9间的 。 数字,则C语言的<无符 状态之间可用有向边连接,其 上标记一字符a∈Σ,表示从有 号数>的文法也是(右线 向边的射出状态出发,识别 性)正规文法(见P49) 字符a后,将进入箭头所指状 态(结点)
3.2.1 由正规文法构造状态转换图 • 程序设计语言的单词都能 用正规文法描述; • 例如,标识符可定义为 <标识符>→<标识符>字母 <标识符>→<标识符>数字 <标识符> →字母 • 若把字母、数字视为终结 符,则上述产生式为(左 线性)正规文法 • 若我们用d表示0-9间的 数字,则C语言的<无符 号数>的文法也是(右线 性)正规文法(见P49) • 一般说来,凡能用正规文法描 述的语言,均可由某种有限状 态算法——状态转换图进行分 析。 • 状态转换图 由有限个结点所 组成的有向图。 • 每个结点代表在识别分析过程 中扫描器所处的状态,其中 含 有一个初始状态和若干个终态。 在图中,状态用圆圈表示,终 态用双层圆圈表示。 • 状态之间可用有向边连接,其 上标记一字符a,表示从有 向边的射出状态出发,识别一 字符a后,将进入箭头所指状 态(结点)
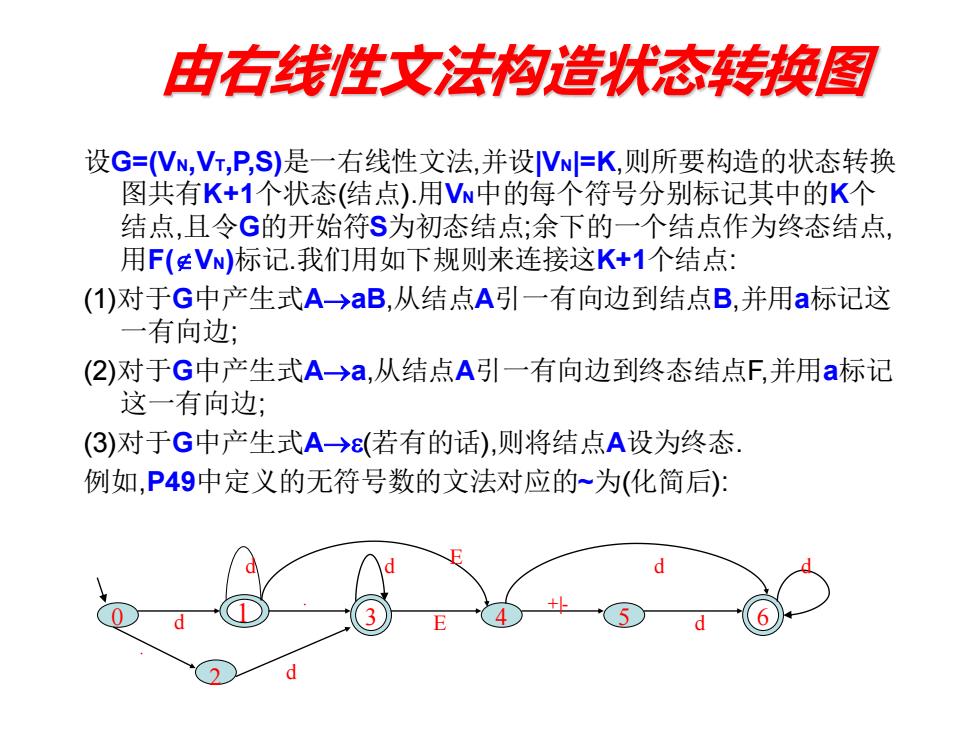
由右线性文法构造状态转换图 设G=(VN,Vī,P,S)是一右线性文法,并设VN=K,则所要构造的状态转换 图共有K+1个状态(结点).用Vw中的每个符号分别标记其中的K个 结点,且令G的开始符S为初态结点;余下的一个结点作为终态结点, 用F(VN)标记.我们用如下规则来连接这K+1个结点: (1)对于G中产生式A→aB,从结点A引一有向边到结点B,并用a标记这 一有向边; (2)对于G中产生式A→a,从结点A引一有向边到终态结点F,并用a标记 这一有向边; (3)对于G中产生式A→(若有的话),则将结点A设为终态 例如,P49中定义的无符号数的文法对应的~为(化简后):
由右线性文法构造状态转换图 设G=(VN,VT,P,S)是一右线性文法,并设|VN|=K,则所要构造的状态转换 图共有K+1个状态(结点).用VN中的每个符号分别标记其中的K个 结点,且令G的开始符S为初态结点;余下的一个结点作为终态结点, 用F(VN)标记.我们用如下规则来连接这K+1个结点: (1)对于G中产生式A→aB,从结点A引一有向边到结点B,并用a标记这 一有向边; (2)对于G中产生式A→a,从结点A引一有向边到终态结点F,并用a标记 这一有向边; (3)对于G中产生式A→(若有的话),则将结点A设为终态. 例如,P49中定义的无符号数的文法对应的~为(化简后): 0 4 5 2 d 1 3 6 . d d d d . E +|- E d d

利用状态转换图识别符号串的方法 对于已给的字符串w=aa2.an,aieV1,利用~对w识别的步 骤如下: (1)从初始状态S出发,自左至右逐个扫描w的各个字符(当 前为a),此时在结点S所射出的诸矢线中,寻找标记为a 的矢线(若不存在,则表明w有语法错误),读入ā并沿矢 线所指方向前进,过渡到下一状态(设为A): (2)设当前处在A状态,所扫描的字符为a,在结点A所射出 的诸矢线中,寻找标记为a的矢线(若不存在,则表明W 有语法错误),读入a+,并进入状态A+1; (3)重复(2),直到w中所有字符被读完且恰好进入终态F时, 宣告整个识别结束,W可被接受. 显然,若我们从初态出发,分别沿一切可能的路径到达终态 结点,并将中径中矢线上所标记的字符依次连接起来,便 得到状态转换图所能识别的全部符号串,这些符号串组 成的集合构成了该~识别的语言
利用状态转换图识别符号串的方法 对于已给的字符串w=a1a2…an,aiVT,利用~对w 识别的步 骤如下: (1)从初始状态S出发,自左至右逐个扫描w的各个字符(当 前为a1),此时在结点S所射出的诸矢线中,寻找标记为a1 的矢线(若不存在,则表明w有语法错误),读入a1并沿矢 线所指方向前进,过渡到下一状态(设为A1). (2)设当前处在Ai状态,所扫描的字符为ai+1,在结点Ai所射出 的诸矢线中,寻找标记为ai+1的矢线(若不存在,则表明w 有语法错误),读入ai+1,并进入状态Ai+1; (3)重复(2),直到w中所有字符被读完且恰好进入终态F时, 宣告整个识别结束,w可被接受. 显然,若我们从初态出发,分别沿一切可能的路径到达终态 结点,并将中径中矢线上所标记的字符依次连接起来,便 得到状态转换图所能识别的全部符号串,这些符号串组 成的集合构成了该~识别的语言

状态转换图与文法雅导 用状态转换图识别符号串w的过程,就是为w建立一个 推导S→*w的过程。 在第一步(在初始状态S下,扫描到a而过渡到下一状 态A),由状态转换图的构造规则可知,G中必有产 生式S→aA;对于识别过程的后续步骤,由状态A识别 a+1后过渡到A恰好对应了使用产生式A→a+1A,, 最后在状态Aa-识别a后到达终态F,对应了使用产生 式 A→a进行推导: ·S→aA1→a1a2A2→…→a1a2…an-1An-1 →a1a2.an
状态转换图与文法推导 • 用状态转换图识别符号串w的过程,就是为w建立一个 推导S* w的过程。 • 在第一步(在初始状态S下,扫描到a1而过渡到下一状 态A1),由状态转换图的构造规则可知,G中必有产 生式S→a1A1;对于识别过程的后续步骤,由状态Ai识别 ai+1后过渡到Ai+1恰好对应了使用产生式Ai →ai+1Ai+1,…, 最后在状态An-1识别an后到达终态F,对应了使用产生 式 A →an进行推导: • S a 1A1a 1a 2A2…… a 1a2…an-1An-1 a 1a2…an