
3.3有限自动机 状态转换图实际上是有限自动机的 图形表示
3.3 有限自动机 状态转换图实际上是有限自动机的 图形表示

3.3.1确定的有限自动机DFA 1抽象地看,状态转换图由五个郁分组成: (1)有限个状态之集,犯作K写 (2)有限个输入符号组成的字母表,犯作 3)从Kx∑到K的转换函数fiK×∑→Kf(p,a)=q表示若 省前状态为P,且输入符号为a,刚进入下一个状态为q日 (4)S0∈K,初始(开始)状态; 5)若干个玲态之集:Z(三K) 由上述五个要素组成的五元式M=(K,∑,S0,Z)称为 一个确定的有限自动机(DFA:Deterministic Finite Automata) 由此可见,一DFA实际上是状态转换图的形式描迷(数学 定义),状态转换图是DFA的几佰(图形)表示
3.3.1 确定的有限自动机DFA 1.抽象地看,状态转换图由五个部分组成: (1)有限个状态之集,记作K; (2)有限个输入符号组成的字母表,记作; (3)从K到K的转换函数 f: K→K. f(p,a)=q表示若 当前状态为p,且输入符号为a,则进入下一个状态为q; (4)S0K,初始(开始)状态; (5)若干个终态之集: Z( K ) 由上述五个要素组成的五元式 M=(K, , f,S0,Z )称为 一个确定的有限自动机 (DFA: Deterministic Finite Automata) 由此可见, 一DFA实际上是状态转换图的形式描述(数学 定义),状态转换图是DFA的几何(图形)表示

DFA的接受集 2.为定义DFA所接受(或识别的符号串集合,我们 先将其转换函数f的定义域拓广到KxΣ*: (1)f^(S,=S,S∈K, 2f(S,w=f(fS,,w,S∈K,a∈2w∈D, 由上面的定义可知,对于x∈*,f6,x)=t的含义是,当M从 状态s出发,依次扫描完x的各个符号后将进入状态t,即只 要f有定义f与的效果是一致的 我们称DFAM接受(或识别某符号串x∈,用状态转换图 来说,就是从初态S出发,经一恰好标有x的路径后可达 到某终态SeZ;用f描述就是:SeZ,fS,x)=S M的接受集我们把一DFAM所接受的符号串的全体称为 M的接受集,记为L(M),即L(MW={x|fSy∈Z,x∈}
DFA的接受集 2.为定义DFA所接受(或识别)的符号串集合,我们 先将其转换函数f 的定义域拓广到K* : (1)f^ (s,)=s, sK; (2)f^ (s,aw)=f^ ( f(s,a),w), sK,a,w*; 由上面的定义可知,对于x* ,f^(s,x)=t 的含义是,当M从 状态s出发,依次扫描完x的各个符号后将进入状态t.即只 要f有定义,f^与f的效果是一致的. 我们称DFA M接受(或识别)某符号串x* ,用状态转换图 来说,就是从初态S0出发,经一恰好标有x 的路径后可达 到某终态SZ ;用f^描述就是: SZ, f(S0,x)=S M的接受集 我们把一DFA M所接受的符号串的全体称为 M的接受集,记为L(M),即 L(M)={ x | f(S0 ,x) Z,x* }

确定的有限自动机 。 我们之所以把前面定义的有限自动机称为确定的 FA,是因为在状态转换的每一步,根据FA当前的 状态及扫描的输入字符,便能唯一地确定FA的下 一状态。在转换图上看,若=n,则任何结点所 引出的矢线至多有条,且矢线上的标记均不同。 ● 例如,P52图3-4所对应的DFA为 M=({R,U,S},{0,1},f,R,S》其中,f的定义如下: f(R,0)=U f(U,0)=U f(U,1)=S f(S,1)=S ● 由DFA与状态转换图的关系可知,构造状态转换 图的算法,同样适用于构造DFA。 ·实际上,我们可以证明,V正规文法G,DFAM, 使L(M)=L(G),反之亦然
确定的有限自动机 • 我们之所以把前面定义的有限自动机称为确定的 FA,是因为在状态转换的每一步,根据FA当前的 状态及扫描的输入字符,便能唯一地确定FA的下 一状态。在转换图上看,若||=n,则任何结点所 引出的矢线至多有n条,且矢线上的标记均不同。 • 例如,P52图3-4所对应的DFA为 M=({R,U,S},{0,1},f,R,{S}) 其中,f的定义如下: f(R,0)=U f(U,0)=U f(U,1)=S f(S,1)=S • 由DFA与状态转换图的关系可知,构造状态转换 图的算法,同样适用于构造DFA。 • 实际上,我们可以证明,正规文法G,DFA M, 使 L(M)=L(G),反之亦然
3.3.2非确定的有限自动机 ·若在一左线性文法中含 有多个右部相同的产生 式,如A→Ua BUaC-→Ua.. X-→Ua, 或在一右线性文法中同 时含有形如 U-→aAU-→aBU→aC . U→aX的产生式, 图3-8NFA的状态转换图 在相应的状态转换图中, 央特买下状碧 就会出现这样的结点U, 不唯一,而是在状态集 它具有多条标记为同一 A,B,C ,中任选其一 ,具 输入符号a的矢线,如 有这种性质的FA称为非确定的 FA (NFA:Nondeterministic 右图所示 FA
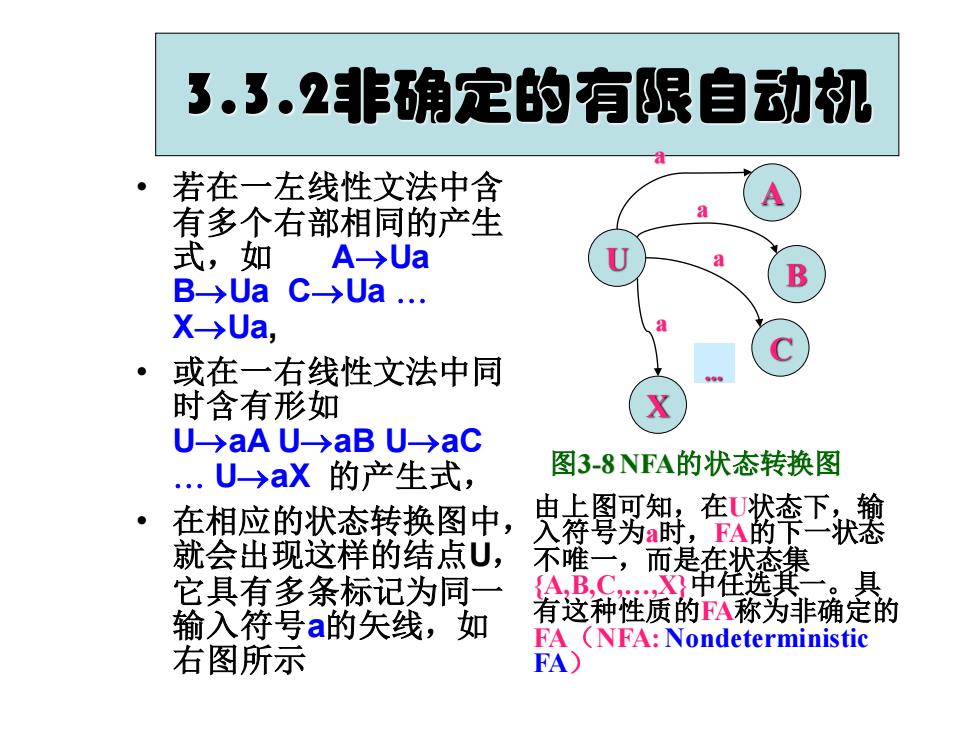
3.3.2非确定的有限自动机 • 若在一左线性文法中含 有多个右部相同的产生 式,如 A→Ua B→Ua C→Ua X→Ua, • 或在一右线性文法中同 时含有形如 U→aA U→aB U→aC U→aX 的产生式, • 在相应的状态转换图中, 就会出现这样的结点U, 它具有多条标记为同一 输入符号a的矢线,如 右图所示 图3-8 NFA的状态转换图 由上图可知,在U状态下,输 入符号为a时,FA的下一状态 不唯一,而是在状态集 {A,B,C,…,X}中任选其一。具 有这种性质的FA称为非确定的 FA(NFA: Nondeterministic FA) U A B C X a a a a