
4 History of Decision Tree Induction .1970s,J.Ross Quinlan,ID3; .E.B.Hunt etc.expanded,C4.5; ●1984,a group of statisticians,.CART .ID3,C4.5,and CART adopt a greedy (i.e., nonbacktracking)approach in which decision trees are constructed in a top-down recursive divide-and-conquer manner. 16 DATA Copyright 2019 by Xiaoyu Li
Copyright © 2019 by Xiaoyu Li. 16 4 History of Decision Tree Induction 1970s, J. Ross Quinlan, ID3; E. B. Hunt etc. expanded, C4.5; 1984, a group of statisticians, CART ID3, C4.5, and CART adopt a greedy (i.e., nonbacktracking) approach in which decision trees are constructed in a top-down recursive divide-and-conquer manner

5 A Basic Algorithm It is with three parameters:D,attribute list,and Attribute selection method. Algorithm:Generate_decision_tree.Generate a decision tree from the training tuples of data partition,D. Input: Data partition,D,which is a set of training tuples and their associated class labels; attribute_list,the set of candidate attributes; Attribute-selection-method,a procedure to determine the splitting criterion that"best" partitions the data tuples into individual classes.This criterion consists of a splitting-attribute and,possibly,either a split-point or splitting subset. Output:A decision tree. 17 Copyright 2019 by Xiaoyu Li
Copyright © 2019 by Xiaoyu Li. 17 5 A Basic Algorithm It is with three parameters: D, attribute_list, and Attribute_selection_method

5 A Basic Algorithm Method: (1) create a node N; (2) if tuples in D are all of the same class,C,then (3) return N as a leaf node labeled with the class C; (4) if attribute_list is empty then (5) return N as a leaf node labeled with the majority class in D;/majority voting (6) apply Attribute_selection_method(D,attribute_list)to find the "best"splitting_criterion; (7) label node N with splitting_criterion; (8) if splitting-attribute is discrete-valued and multiway splits allowed then//not restricted to binary trees (9) attribute-list +attribute-list-splitting-attribute;/remove splitting-attribute (10)for each outcome j of splitting-criterion /partition the tuples and grow subtrees for each partition (11) let D be the set of data tuples in D satisfying outcome j;/a partition (12) if D;is empty then (13) attach a leaf labeled with the majority class in D to node N; (14) else attach the node returned by Generate_decision-tree(Di,attribute_list)to node N; endfor (15) return N; Copyright 2019 by Xiaoyu Li
5 A Basic Algorithm Copyright © 2019 by Xiaoyu Li
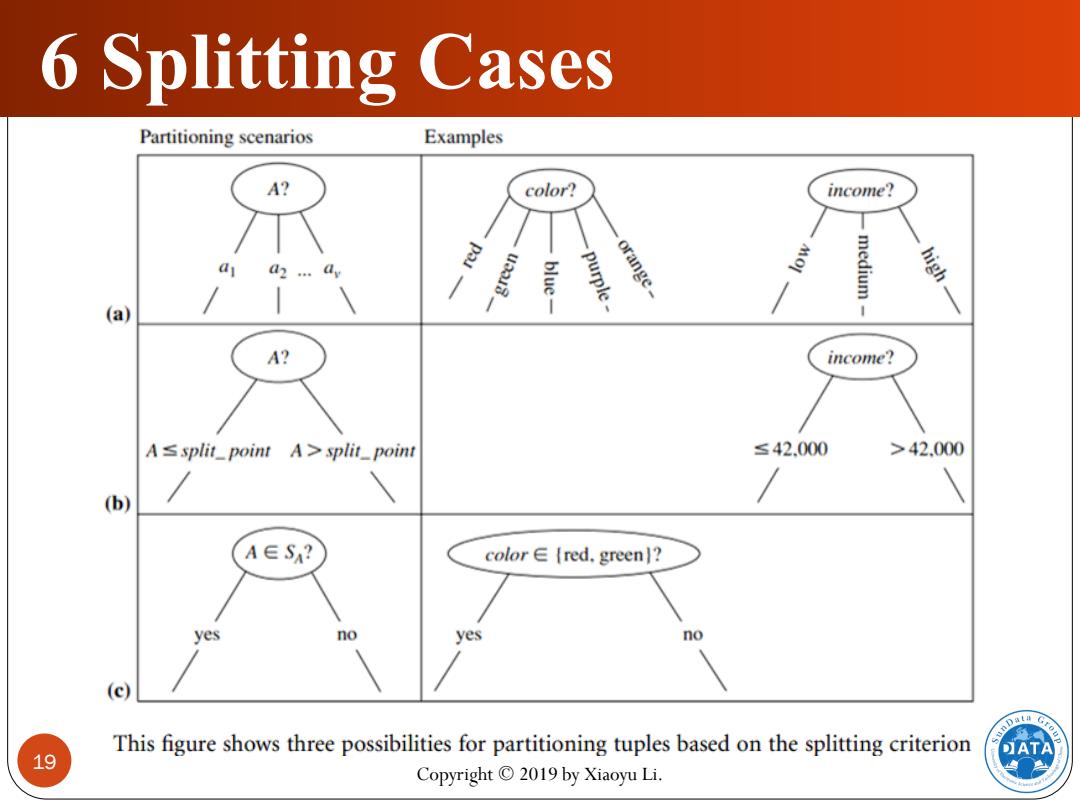
6 Splitting Cases Partitioning scenarios Examples A? color? income? a2...dy purple orange- medium (a) A? income? A ssplit_point A>split_point ≤42.000 >42.000 (b) A∈SA? color∈{red.green]? yes no yes no (c) This figure shows three possibilities for partitioning tuples based on the splitting criterion 19 Copyright 2019 by Xiaoyu Li
19 6 Splitting Cases Copyright © 2019 by Xiaoyu Li

6 Splitting Cases I.A is discrete-valued:In this case,the outcomes of the test at node N correspond directly to the known values of A.A branch is created for each known value, aj,of A and labeled with that value (Figure 8.4a).Partition Di is the subset of class-labeled tuples in D having value aj of A.Because all the tuples in a given partition have the same value for A,A need not be considered in any future partitioning of the tuples.Therefore,it is removed from attribute list (steps 8 and 9). A? color? income? a red -green blue purple orange medium 20 Copyright 2019 by Xiaoyu Li
20 6 Splitting Cases Copyright © 2019 by Xiaoyu Li