
固体的热导率 固体热导率 k=3c,1 金属中能量传递既有电子运动,又有声子运动 在大多数纯导体中, 液氮温度以上:电子运动所占能量远大于声子运动。电子比热与绝 对温度T成正比,该温区上电子平均自由程与T成反比。由于密度和 平均电子速度只是温度的弱函数因而电导体的热导率在液氮温度 以上几乎是定值 液氨温度以下时,声子对比热的贡献变得越来越明显,在这个温度 范围内,纯金属的热导率与T2成正比 温度进一步降低,热导率将达到一最大值,直至能量载流子的平均自 由程达到试样尺度 在绝对零度附近极低温区内,热导率将随温度下降而下降(比热→0)。 合金和不纯金属的热导率随温度下降而下降,合金中不会有最大值现象 上游充通大学 2018年3月6日 16 SHANGHAI JLAO TONG UNIVERSITY
2018年3月6日 16 固体的热导率 固体热导率 k c v t v 1 3 金属中能量传递既有电子运动,又有声子运动 液氮温度以上:电子运动所占能量远大于声子运动。电子比热与绝 对温度T成正比,该温区上电子平均自由程与T成反比。由于密度和 平均电子速度只是温度的弱函数,因而电导体的热导率在液氮温度 以上几乎是定值 在大多数纯导体中, 液氮温度以下时,声子对比热的贡献变得越来越明显,在这个温度 范围内,纯金属的热导率与T-2成正比 温度进一步降低,热导率将达到一最大值, 直至能量载流子的平均自 由程达到试样尺度 在绝对零度附近极低温区内,热导率将随温度下降而下降 (比热0)。 合金和不纯金属的热导率随温度下降而下降,合金中不会有最大值现象
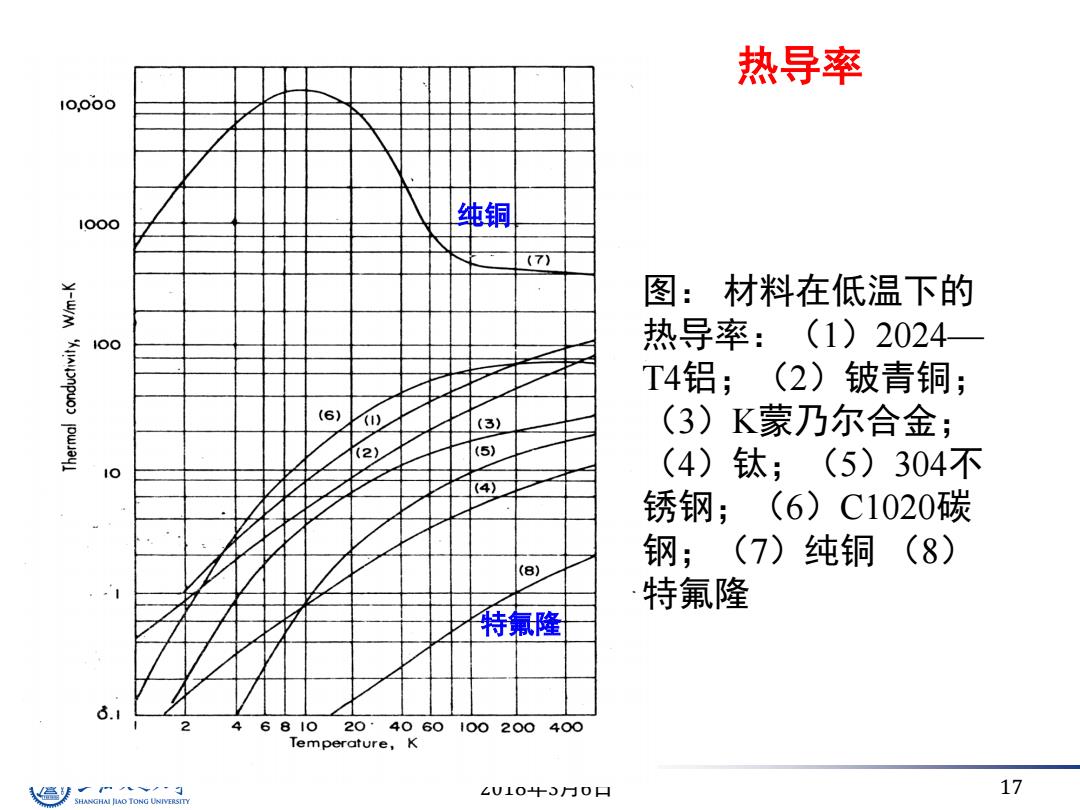
热导率 10,000 1000 纯铜 (7) -w/M 图:材料在低温下的 1○0 热导率:(1)2024一 T4铝;(2)铍青铜; (6) (1) (3) (3)K蒙乃尔合金; (2) (5) (4)钛;(5)304不 (4) 锈钢;(6)C1020碳 钢;(7)纯铜(8) (B) 特氟隆 特氟隆 6.1 2 4 681020·4060100200400 Temperature,K ∠U10+5月0口 17
2018年3月6日 17 热导率 图: 材料在低温下的 热导率:(1)2024— T4铝;(2)铍青铜; (3)K蒙乃尔合金; (4)钛;(5)304不 锈钢;(6)C1020碳 钢;(7)纯铜 (8) 特氟隆 纯铜 特氟隆

热导率计算示例 例求空气在250K和101.3kPa时的热导率。已知:平均自 由程为49nm,空气气体常数为287J/kg-K,绝热指数为1.4, 定容比热为716.5J/kg-K。 解: 由于气体压力低于临界压力,因此可由理想气体方程计算空气的密度: p=P=1013×10 RT287×250 =1.412g/m3 由公式(2.4),分子平均速度为: D=8×287×250)=427.4m1s π 由公式(2.3),气体热导率为: (9x14-5)×1412×716.5×427.4×49×10=2.013x102W1m-K=20.13mw1 空气在250K时实验测得的热导率为22.27mWm-K,理论计算值与之比较相差10%左右。 上游气通大学 2018年3月6日 18 SHANGHAI JLAO TONG UNIVERSITY
2018年3月6日 18 热导率计算示例 例 求空气在250K和101.3kPa时的热导率。已知:平均自 由程为49nm,空气气体常数为287J/kg-K,绝热指数为1.4, 定容比热为716.5J/kg-K。 解: 由于气体压力低于临界压力,因此可由理想气体方程计算空气的密度: p RT kg m 101 3 10 287 250 1 412 3 3 . . / 由公式(2.4),分子平均速度为: v m s ( ) . / 8 287 250 / 427 4 1 2 由公式(2.3),气体热导率为: kt W m K mW m K 1 8 9 1 4 5 1 412 716 5 427 4 49 10 2 013 10 20 13 9 2 ( . ) . . . . / . / 空气在250K时实验测得的热导率为22.27mW/m-K, 理论计算值与之比较相差10%左右

固体的比热 物体的比热被定义为使单位质量的物体温度上升一度所需的能量 定压比热(C);定容比热(C) 对常压下的固体和液体,两种比热值相差很小,而对于气体 却有很大差别 运用统计学和量子理论就可以较为精确地计算 固体比热随温度的变化,Debye模型给出了令人满意的解释 假设固体是一个连续介质 定义Oo是Debye特征温度 6 h是普朗克常数;v,是固体内的声速;k是玻尔兹曼常数;N/V是固体单位体积原子数 上游充通大学 2018年3月6日 19 SHANGHAI JLAO TONG UNIVERSITY
2018年3月6日 19 固体的比热 物体的比热被定义为使单位质量的物体温度上升一度所需的能量 定压比热(cp);定容比热(cv) 对常压下的固体和液体,两种比热值相差很小,而对于气体 却有很大差别 运用统计学和量子理论就可以较为精确地计算 固体比热随温度的变化,Debye模型给出了令人满意的解释 假设固体是一个连续介质 定义θD是Debye特征温度 D hva k N V ( ) 3 / 4 1 3 h是普朗克常数;va是固体内的声速;k是玻尔兹曼常数;N/V是固体单位体积原子数
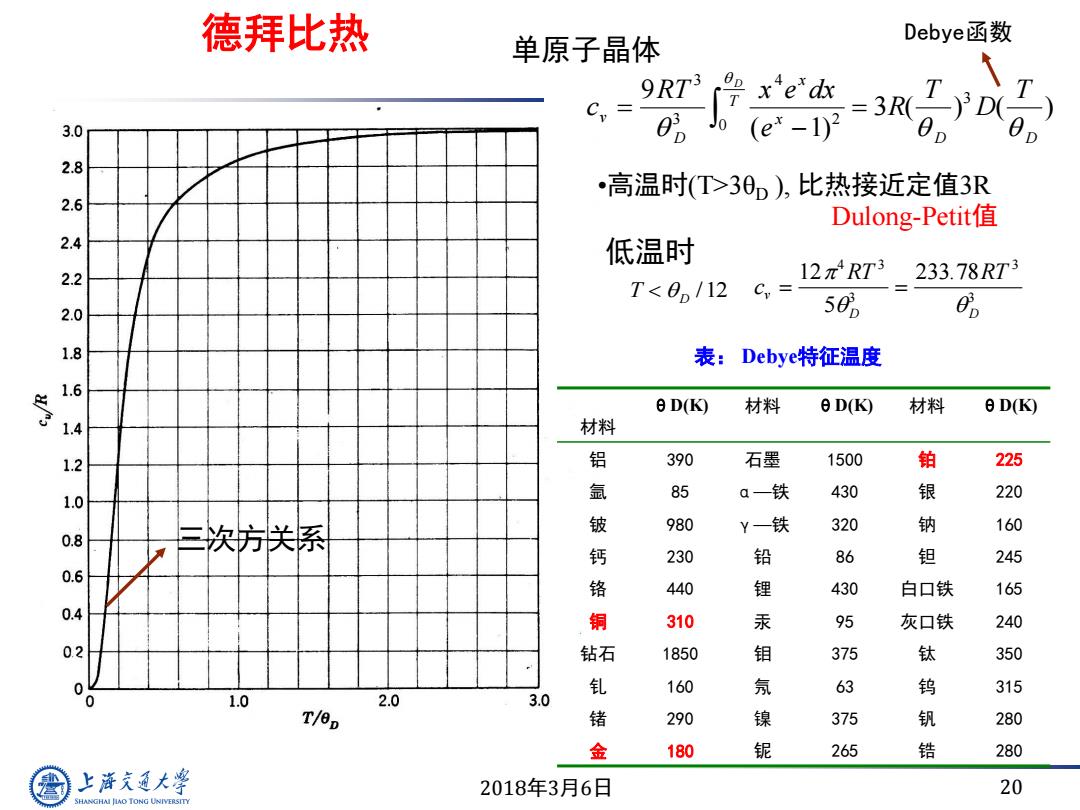
德拜比热 单原子晶体 Debyer函数 3.0 2.8 ·高温时(T>30D),比热接近定值3R 2.6 Dulong-Petit值 2.4 低温时 2.2 12πRT3 233.78RT3 T<0。/12 C= 2.0 50 8 1.8 表:Debye特征温度 1.6 e D(K) 材料 D(K) 材料 e D(K) 1.4 材料 1.2 铝 390 石墨 1500 铂 225 1.0 氩 85 a一铁 430 银 220 0.8 三次方关系 铍 980 Y一铁 320 钠 160 钙 230 铅 86 钽 245 0.6 铬 440 锂 430 白口铁 165 0.4 铜 310 汞 95 灰口铁 240 02 钻石 1850 钼 375 钛 350 0 钆 160 氖 63 钨 315 1.0 2.0 3.0 T/ep 锗 290 镍 375 钒 280 金 180 铌 265 锆 280 上降充通大学 2018年3月6日 20 SHANGHAI JIAO TONG UNIVERSITY
2018年3月6日 20 德拜比热 c RT x e dx e R T D T v D x x D D T D 9 1 3 3 3 4 2 3 0 ( ) ( ) ( ) •高温时(T>3θD ), 比热接近定值3R T D /12 c RT RT v D D 12 5 233 78 4 3 3 3 3 . 表: Debye特征温度 材料 θD(K) 材料 θD(K) 材料 θD(K) 铝 390 石墨 1500 铂 225 氩 85 α—铁 430 银 220 铍 980 γ—铁 320 钠 160 钙 230 铅 86 钽 245 铬 440 锂 430 白口铁 165 铜 310 汞 95 灰口铁 240 钻石 1850 钼 375 钛 350 钆 160 氖 63 钨 315 锗 290 镍 375 钒 280 金 180 铌 265 锆 280 单原子晶体 Debye函数 Dulong-Petit值 低温时 三次方关系