惰性气体固体 •正原子核位于中心,电子电荷分布平均为球对称 )=0 ·但热涨落(有限T)产生瞬间电偶极子 P(t)≠0 D P=0 P≠0 涨落 ·如果偶极子是随机的话,一个近邻原子不存在净作用力 (时间平均 ·但偶极子诱导最近邻原子产生的偶极子总是给出吸引力 黄春晖编著 6
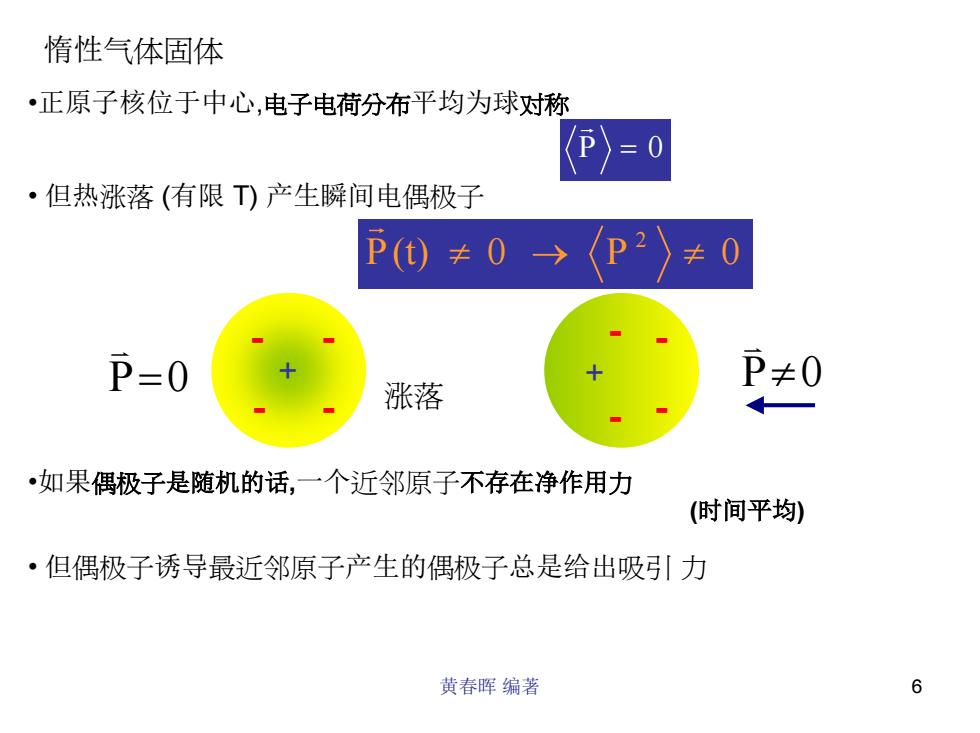
黄春晖 编著 6 惰性气体固体 •正原子核位于中心,电子电荷分布平均为球对称 P = 0 r • 但热涨落 (有限 T) 产生瞬间电偶极子 P (t) 0 P 0 2 ≠ → ≠ r - - - - + - - - - + P≠0 v P=0 v 涨落 •如果偶极子是随机的话,一个近邻原子不存在净作用力 (时间平均) • 但偶极子诱导最近邻原子产生的偶极子总是给出吸引 力

两个理想的谐振子 X2 X1 +e00o000m-e +e000000m-e R P1和P2是这两个振子的动量 C是力常数 不受微扰的哈密顿-没有库仑相互作用 H。=D+Cx+ 2m 2 m 系统的库仑相互作用能的哈密顿项 e H e2 e e2 2e'x X2 R R+x-x2 R+X1 R-X2 xX2<<R R3 黄春晖编著
黄春晖 编著 7 惰性气体固体模型– 两个理想的谐振子 R x2 +e -e x1 +e -e p1 和 p2是这两个振子的动量 C是力常数 不受微扰的哈密顿– 没有库仑相互作用 2 2 2 2 2 1 2 1 o Cx 21 2mp Cx 21 2mp H = + + + 系统的库仑相互作用能的哈密顿项 3 1 2 2 x , x R R 2e x x 1 2 → − << 2 2 1 2 1 2 2 2 1 R x e R x e R x x e R e H − − + − + − = +
简正模式变换-对称(s)和反-对称(a) x.-XitX2:X.=X-X2 √2 P,=Pu+p2. √2 √2 经过变换后的总哈密顿量 2e2 2e2 H= 2m 2 R3 2m R3 H。=+++cx 2m2 2m2 m 黄春晖编著 8
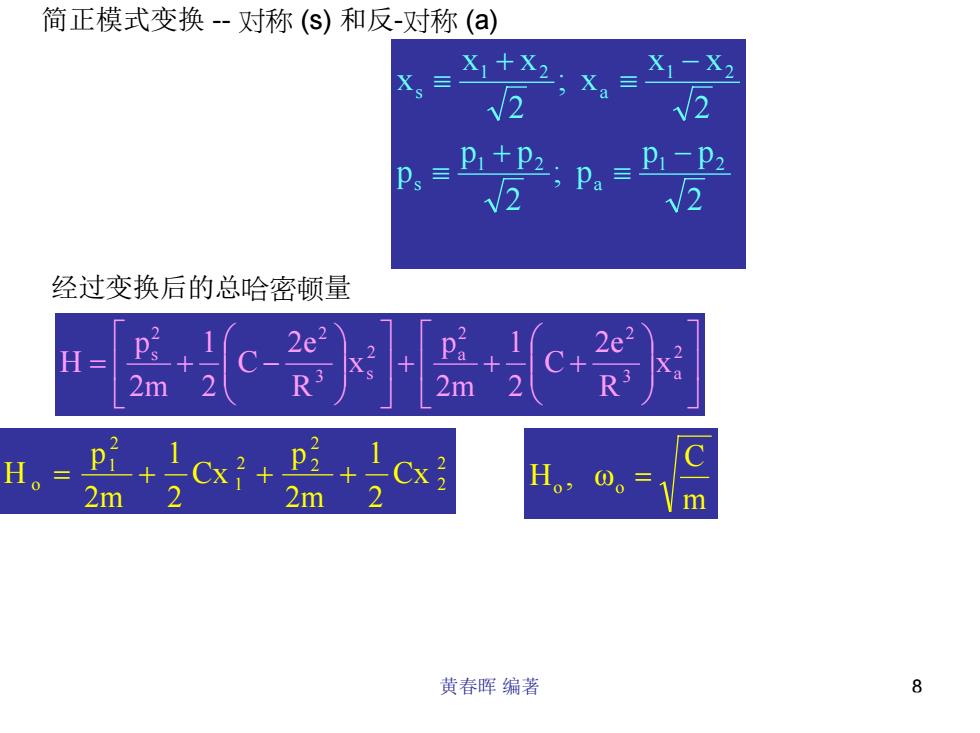
黄春晖 编著 8 简正模式变换 - 对称 (s) 和反-对称 (a) 2 p p ; p 2 p p p 2 x x ; x 2 x x x 1 2 a 1 2 s 1 2 a 1 2 s − ≡ + ≡ − ≡ + ≡ 经过变换后的总哈密顿量 + + + = + − 2 3 a 2 2 2 a 3 s 2 2 s x R2e C 21 2mp x R2e C 21 2mp H 2 2 2 2 2 1 2 1 o Cx 21 2mp Cx 21 2mp H = + + + mC Ho , ωo = m C 2e / R m C ω m C 2e / R m C H , ω 2 3 a a 2 3 s s + = = − 藕合振子的两个频率 = = 对称 (s) 和反-对称 (a)
零点能量 >非藕合振子 。h。+。ho。 1 > 藕合振子 h0+h0。 C-2e2/R3 m C+2e2/R3 m 因此,藕合振子的零点能量 低于没藕合振子的零点能量 1 2e2 △U= ×2 A ho 吸引相互作用 2 8 CR3 9
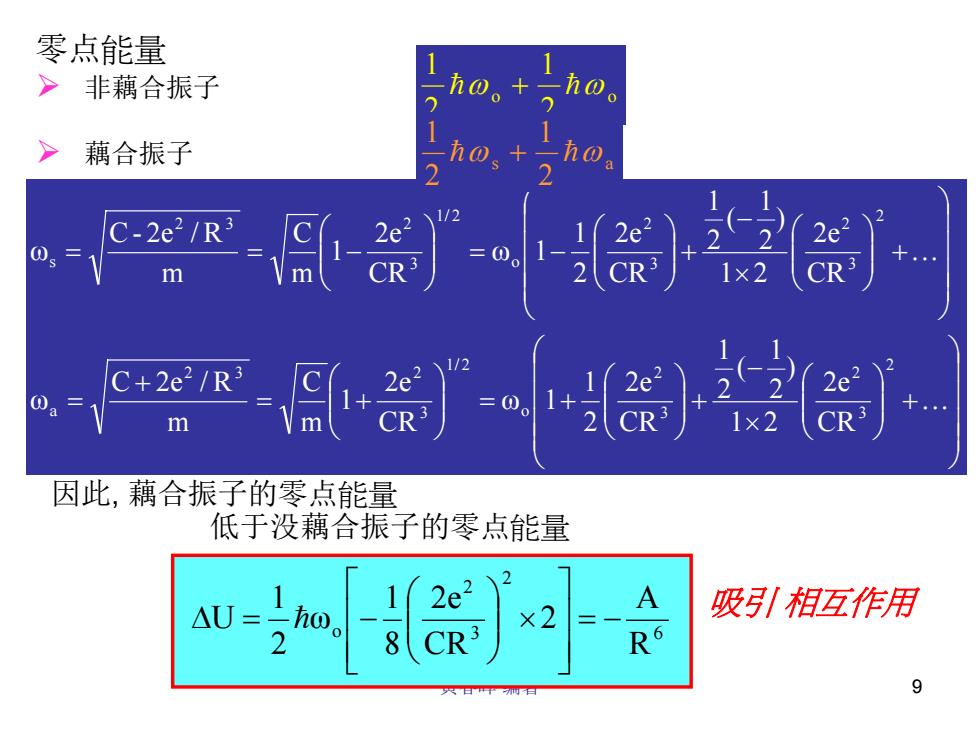
黄春晖 编著 9 + × − + = + = + + = + × − + = − = = − K K 2 3 2 3 2 o 1/ 2 3 2 3 2 a 2 3 2 3 2 o 1/ 2 3 2 3 2 s CR 2e 1 2 ) 2 1 ( 2 1 CR 2e 2 1 ω 1 CR 2e 1 m C m C 2e / R ω CR 2e 1 2 ) 2 1 ( 2 1 CR 2e 2 1 ω 1 CR 2e 1 m C m C - 2e / R ω 因此, 藕合振子的零点能量 低于没藕合振子的零点能量 o o 2 1 2 1 h ω + h ω s a 2 1 2 1 h ω + h ω 零点能量 ¾ 非藕合振子 ¾ 藕合振子 6 2 3 2 o R A 2 CR 2e 8 1 ω 2 1 U = − × ∆ = h − 吸引 相互作用
van der Waals相互作用,London相互作用, 诱导偶极子-偶极子相互作用 A △U= <0 R6 A= =ho,a2 这里α是电极化率 原子的“极化” P=aE 涨落 诱导 P -X <0 R3 黄春晖编著 10
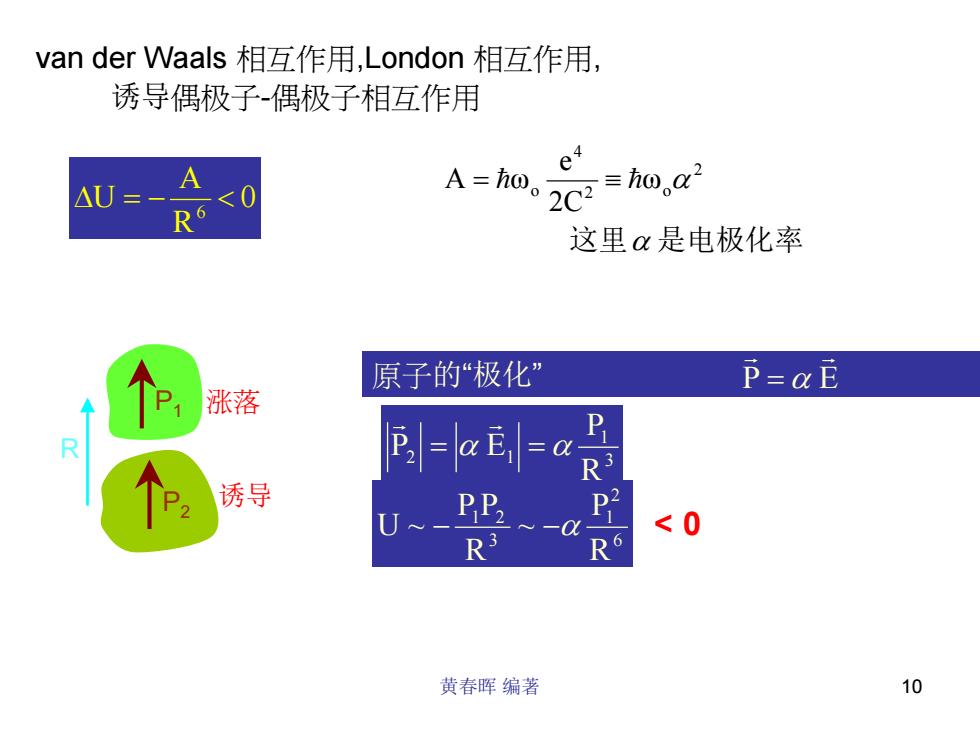
黄春晖 编著 10 van der Waals 相互作用,London 相互作用, 诱导偶极子-偶极子相互作用 这里 是电极化率 ω 2C e A ω 2 2 o 4 o α = h ≡ h α 0 R A U 6 ∆ = − < P2 诱导 P1 涨落 P E r r 原子的“极化” =α 3 1 2 1 R P P = α E =α r r 6 2 1 3 1 2 R P ~ R P P U ~ − −α R < 0