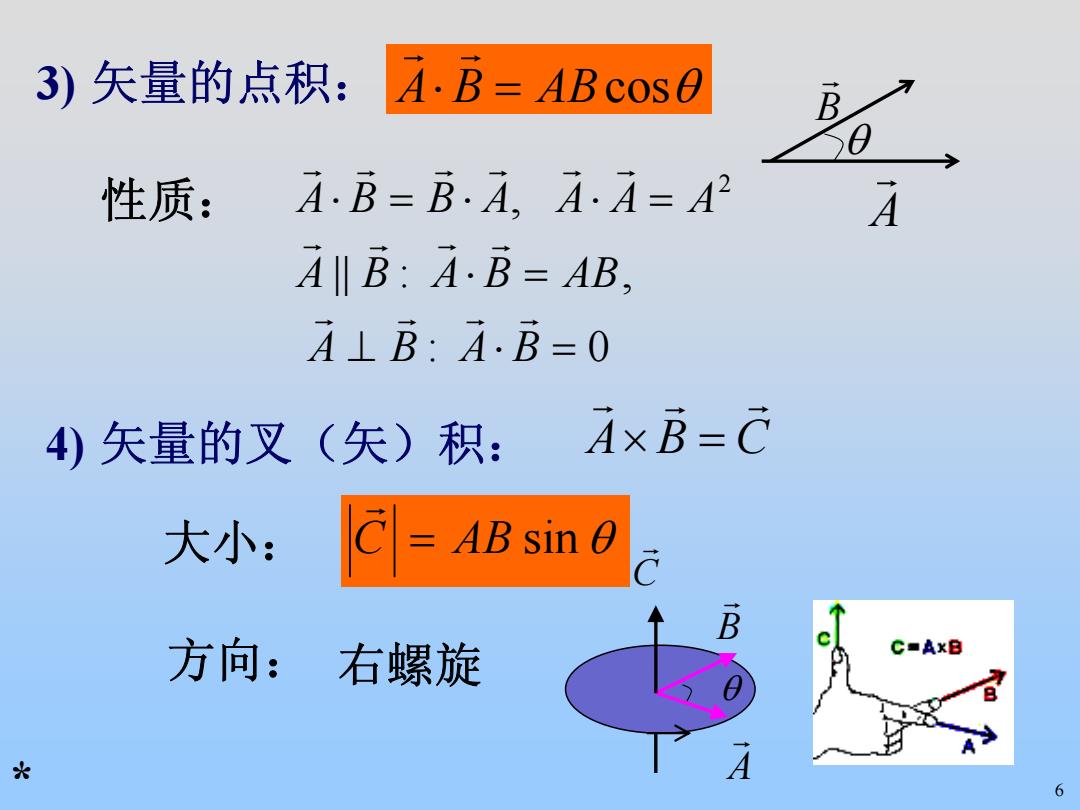
3)矢量的点积: 4.B=ABcos0 B 性质: 4.B=B.A.A.A=A2 A A‖B:AB=AB, A⊥B:A.B=0 4)矢量的叉(矢)积: AxB=C 大小: C=ABsin0 方向:右螺旋 C■AxB 光 A 6
6 3) 矢量的点积: 4) 矢量的叉(矢)积: 大小: 方向: A r B r θ =⋅ ABBA cosθ r r CBA r r r =× = ABC sin θ r 右螺旋 性质: 0 : :|| , , 2 =⋅⊥ =⋅ =⋅⋅=⋅ BABA ABBABA AAAABBA r r r r r r r r r r r r r r A r B r θ C r *

性质:AxB=-BxA, A‖B:A×B=0, A⊥B:|A×B=AB 5)矢量的直角分量表示: A=Ai+Aj+A.k Z Ai:沿x轴分矢量 A:沿x轴分量 y X 7
7 性质: ABBABA BABA ABBA =×⊥ =× ×−=× || : , :|| , r r r r r r r r r r r r 0 5) 矢量的直角分量表示: x y zkAjAiAA r r r r ++= x :沿xiA 轴分矢量 r x :沿xA 轴分量 A x A z A y x y z A r i r j r k r

矢量的模:A=√A?+A+A经 A 矢量的方向余弦: y X cos2a+cos2 B+cos2y =1 矢量运算的直角分量表示 A=Ai+4j+A.k B=Bi+Bj+B. A±B=(A±B)i+(A±B,)j+(A.±B)k A·B=A,B+A,B+AB Ax B=(A,B.-A.B)i+(A.B,-AB.)j(AB,-A,B.)k 8
8 xx yy zz kBAjBAiBABAr r r r r ±+±+±=± )()()( ++=⋅ BABABABA zzyyxx r r yzzy zxxz xyyx kBABAjBABAiBABABAr r r r r ( () () −+−+−=× ) x y zkBjBiBBr r r r ++= 矢量的模: 222 ++= AAAA zyx 矢量的方向余弦: Ax Az Ay x y z A r α β γ 1 2 2 2 =++ = = = γβα α β γ coscos cos A A cos , A A cos , cos y z A A x 矢量运算的直角分量表示 x y zkAjAiAAr r r r ++=
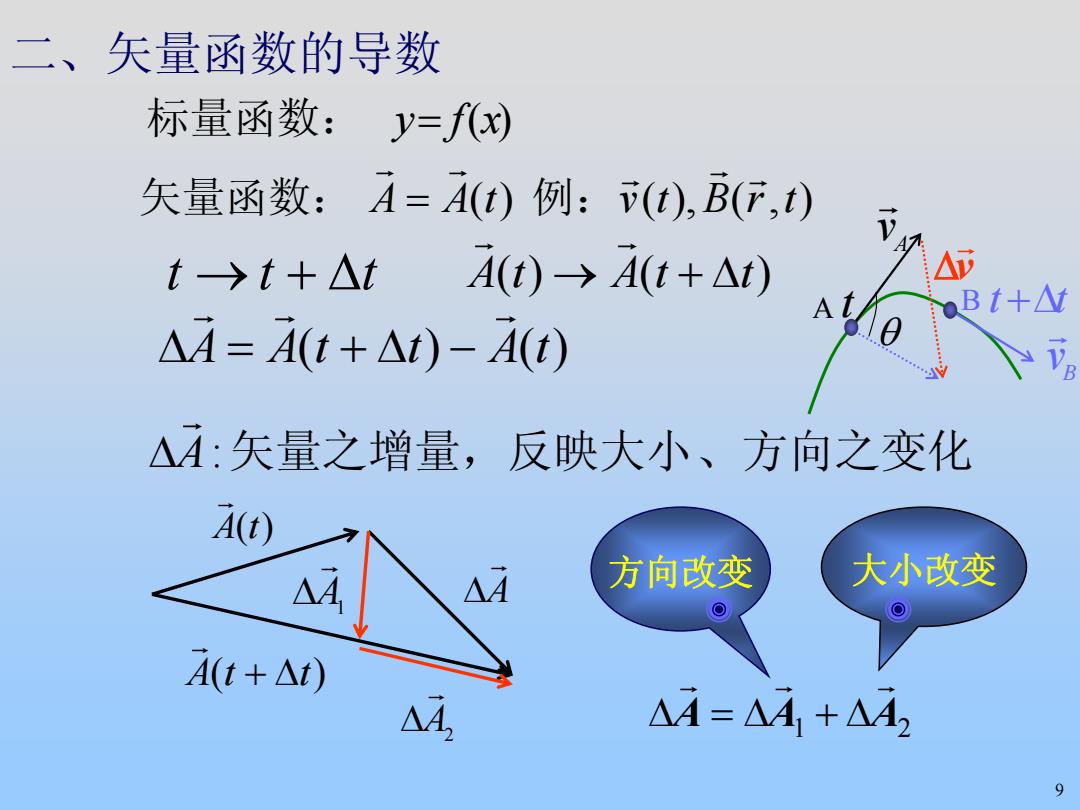
二、矢量函数的导数 标量函数:y=f() 矢量函数:A=A(t)例:(t),B(行,t) t>t+△t A(t)→A(t+△t) △ oBt+△t △A=A(t+△t)-A(t) △A:矢量之增量,反映大小、方向之变化 A() △4 △4 方向改变 大小改变 A(t+△t) △A=△41+△42 9
9 二、矢量函数的导数 标量函数: = xfy )( trBtvtAA ),(),( )( r r r r r 矢量函数: = 例: t → t + Δ t Δ+→ ttAtA )()( r r tAttAA )()( r r r −Δ+=Δ A:矢量之增量,反映大小、方向之变化 r Δ tA )( r Δ+ ttA )( r A r Δ A2 r Δ A1 r Δ AAA 21 r r r Δ+Δ=Δ 方向改变 大小改变 A t A v r θ v r Δ B t + Δt Bv r
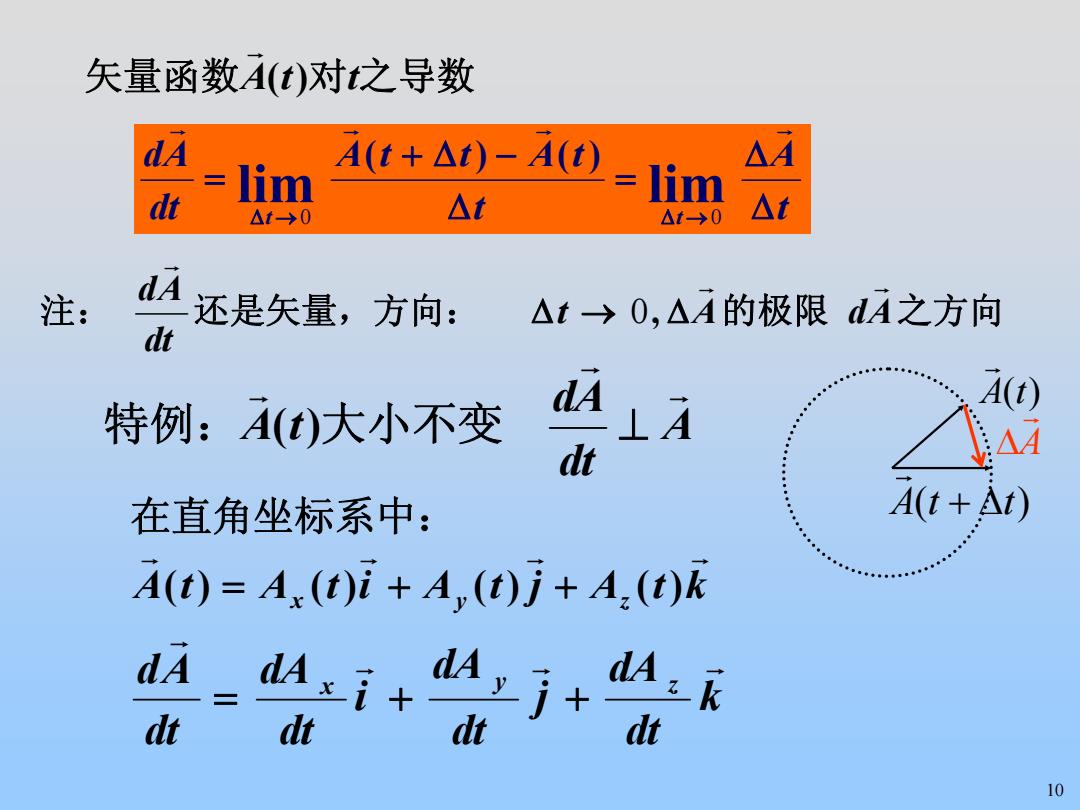
矢量函数A(t)对t之导数 dA lim At+△)-A(四=]im △A t→0 △t △1→0 △t 注: 还是矢量,方向: △t→0,△A的极限dA之方向 dt 特例:A(t)大小不变 dA ⊥A A(+) dt △4 在直角坐标系中: A(t+At) A(t)=A,(t)i+A,(t)j+A.(t)k dA A:k dt dt dt dt 10
10 矢量函数 )( 对ttA 之导数 r t A t tAttA dt Ad t t Δ Δ = Δ −Δ+ = →Δ →Δ r r r r lim lim )()( 0 0 注: 还是矢量,方向: 的极限 AdAt 之方向 dtAd r r r 0, Δ→Δ A dt Ad tA r r r 特例: )( 大小不变 ⊥ x y z ktAjtAitAtA r rrr ++= )()()()( 在直角坐标系中: k dt dA j dt dA i dt dA dtAd x y z rrr r ++= tA )( r Δ+ ttA )( r A r Δ