
第上章图
第七章 图

√7.1图的抽象数据类型定义 7.2图的存储表示 7.3图的遍历 7.4最小生成树 7.5拓扑排序 7.6关键路径 7.7两点之间的最短路径问题
7.1 图的抽象数据类型定义 7.2 图的存储表示 7.3 图的遍历 7.4 最小生成树 7.7 两点之间的最短路径问题 7.5 拓扑排序 7.6 关键路径

7.1图的抽象数据类型定义 一、图的结构定义 二、名词和术语 三、基本操作
7.1 图的抽象数据类型定义 一、图的结构定义 二、名词和术语 三、基本操作
、 图的结构定义 图是由一个顶点集V和一个弧集VR构成的数 据结构。 Graph =(V,VR) V是顶点的有穷非空集合, VR是两顶点间关系的集合。 其中,VR={<V,w>|V,w∈V且P(W,w)} <y,w>表示从v到w的一条弧,并称v为弧尾, w为弧头。 谓词Py,w定义了弧<y,w>的意义或信息
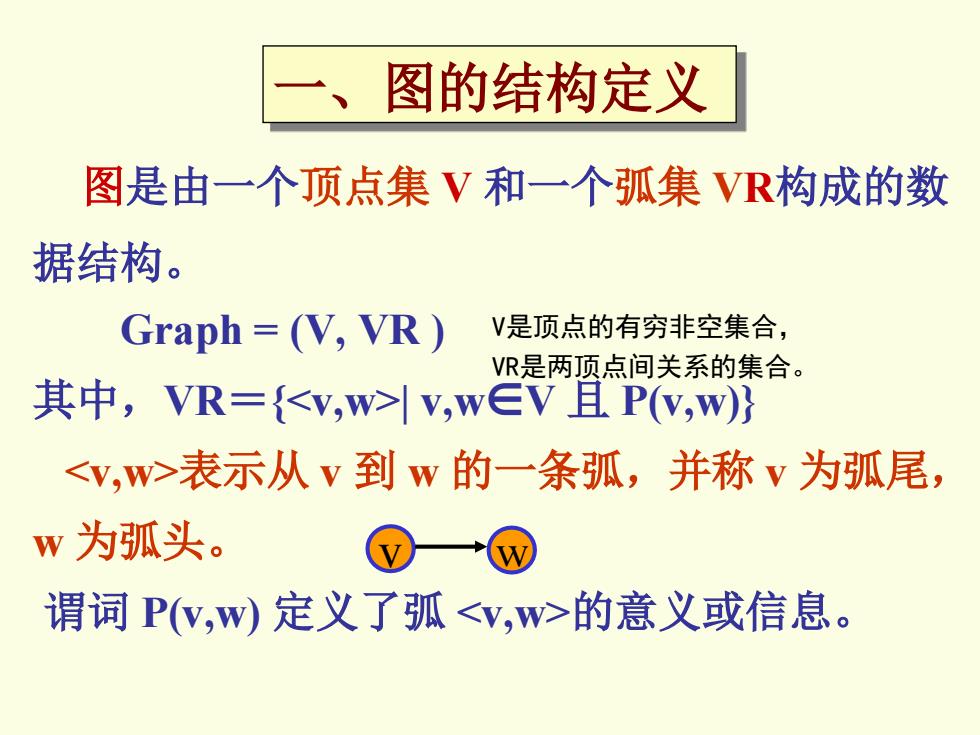
图是由一个顶点集 V 和一个弧集 VR构成的数 据结构。 Graph = (V, VR ) 其中,VR={<v,w>| v,w∈V 且 P(v,w)} <v,w>表示从 v 到 w 的一条弧,并称 v 为弧尾, w 为弧头。 谓词 P(v,w) 定义了弧 <v,w>的意义或信息。 V是顶点的有穷非空集合, VR是两顶点间关系的集合。 v w 一、图的结构定义

二、名词和术语 1.有向图:由于“弧”是有方向的,因此 称由项点集和弧集构成的图为有向图。 例如:G1=(V1,VR1) 其中 V=A,B,C,D,E VR={<A,B>,<A,E>, E <B,C>,<C,D>,<D,B> <D,A>,<E,C>}
由于“弧”是有方向的,因此 称由顶点集和弧集构成的图为有向图。 E A C B D 例如: G1 = (V1 , VR1 ) 其中 V1={A, B, C, D, E} VR1={<A,B>, <A,E>, <B,C>, <C,D>, <D,B>, <D,A>, <E,C> } 1.有向图: 二、名词和术语