
1-1-2-1 Newton--Raphson迭代法 问题的提出 例:已知醋酸HAc浓度为c的溶液,求其pH 解:HAc稀溶液中存在: HAc台Ht+Ac K,=[HIAc (1) [HAc] H,O台Ht+OH Kw=[H*][OH-] (2) 国 质量平衡: c=[HAc]+[Ac 电荷平衡: [H*]=[Ac ]+[OH 将Ac,HAc代入(1)1 =HKIH']-[OH-) c-[H]+[OH] (3) 画 将OH=KHI代入(3) [H*]+K[H*]-(Kc+Kw)[H*]-KKw=0 解上述方程得H] pH =-log[H*]
例:已知醋酸HAc浓度为c的溶液,求其pH 解:HAc稀溶液中存在: H O H OH w [H ][OH ] (2) (1) [HAc] [H ][Ac ] HAc H Ac 2 + − + − + − + − ⇔ + = ⇔ + = K Ka 质量平衡: 电荷平衡: [H ] [Ac ] [OH ] [HAc] [Ac ] - = + = + + − − c (3) [H ] [OH ] [H ]([H ] [OH ]) + − + + − − +− = c 将 Ka [Ac-],[HAc]代入(1) 将[OH-]=Kw/[H+]代入(3) [H ] [H ] ( )[H ] 0 w w 3 2 + − + − = + + + Ka Kac K KaK 解上述方程得[H+] pH log[H ] + = − 1-1-2-1 Newton-Raphson迭代法——问题的提出

1-1-2-2 Newton--Raphson:迭代法 方法原理 有非线性N次方程式 f(x)=a0+a1x+a2x2+…= ◆ Newton法适用条件一 (1)f”)有明确表示式且容易计算 f(x)=0 (2)容易确定根的初值x 里 在x=xa附近进行泰勒(Taylor)级数展开 f(x)=f(xo)+(x-xo)f'(xo)+ 21 忽略二阶以上的&误差项 ◆Newton公式 量 f(xo) Xm Xn-1- f(xn-1 f'(xo) f'(xm-1) n次迭代 X2 f(x) f(x)
1-1-2-2 Newton-Raphson迭代法——方法原理 有非线性 N次方程式 ( ) 0 2 f x = a 0 + a1 x + a 2 x + ⋅ ⋅ ⋅ = 在x=x 0 - ε 0附近进行泰勒(Taylor)级数展开 ( 1 ) f ’(x )有明确表示式且容易计算 ( 2)容易确定根的初值x 0 = + − ′ + − ′′ + ⋅⋅⋅ + ( − ) ( ) + ⋅⋅⋅ ! 1 ( ) ( ) 2! 1 ( ) ( ) ( ) ( ) 0 0 0 2 0 0 0 0 x x f x n f x f x x x f x x x f x n n 忽略二阶以上的 ε 0误差项 ( ) ( ) 0 0 0 f x f x x x ′ = − ,L ( ) ( ) ( ) ( ) 1 1 2 1 0 0 1 0 f x f x x x f x f x x x ′ = − ′ = − ◆ Newton法适用条件—— f ( x ) = 0 ( ) n次迭代 ( ) 1 1 1 − − − ′ = − n n n n f x f x x x ◆ Newton公式——
1-1-2-2 Newton--Raphson:迭代法 方法原理 ◆几何意义: 切线法 y=f(x) f(xo) X0-X1= tg a f'(xo) 面 x1=X0- f(xo) f'(x) f(x) X2=X1 f'(x) 判据: Xn --1<EPS (EPS取10-5)
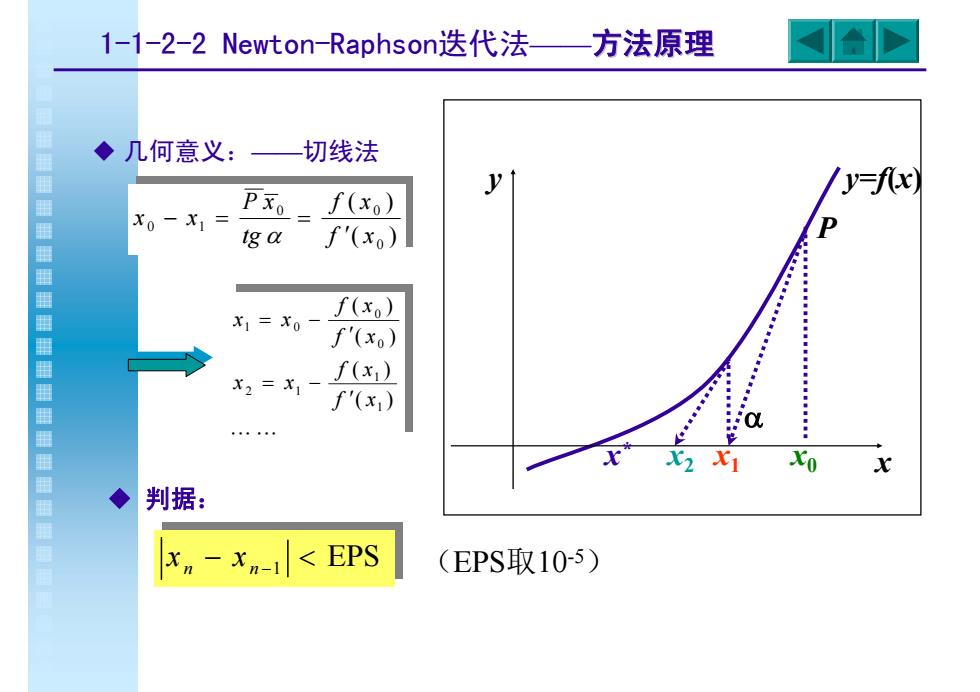
(EPS取10 x n − x n −1 < EPS -5) ◆ 判据: ◆ 几何意义:——切线法 x y y=f(x) x x2 x1 x0 * P α L L ( ) ( ) ( ) ( ) 1 1 2 1 0 0 1 0 f x f x x x f x f x x x ′ = − ′ = − ( ) ( ) 0 0 0 0 1 f x f x tg P x x x ′ − = = α 1-1-2-2 Newton-Raphson迭代法——方法原理