1-1-1-2二分法— 方法原理 计算步骤: a+b 里 1.取x的初值 X0= 2 (对分) 里 计算函数x)值,若xo)KEPS, (EPS为105),则 x为所求之根。 里 2若1xo)>EPS,计算并比较函数值,I 取与x)异号的区间 里 为新的区间,(可能为[xob]或[a,xoJ),如图) 1 画 [a.xo] [xo.b] 判据: b-a<EPS (EPS取105)
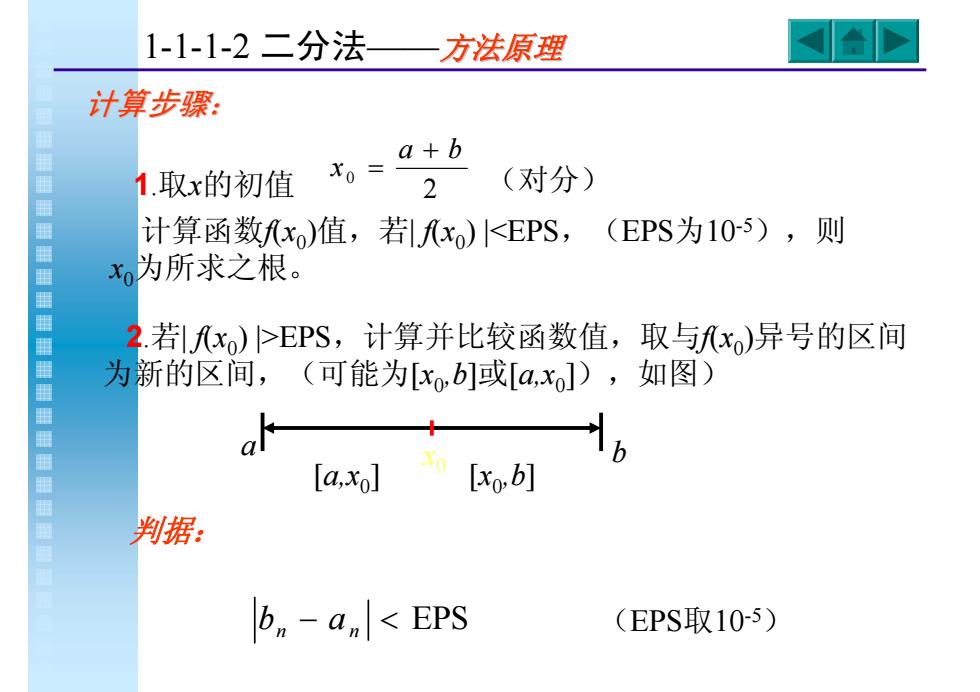
计算步骤: 1.取x的初值 计算函数f(x0)值,若| f(x0) |<EPS,(EPS为10-5),则 x0为所求之根。 2 0 a b x + = (对分) 2.若| f(x0) |>EPS,计算并比较函数值,取与f(x0)异号的区间 为新的区间,(可能为[x0,b]或[a,x0]),如图) a [a,x0] [x0,b] x b 0 (EPS取10 bn − an < EPS -5) 判据: 1-1-1-2 二分法——方法原理
1-1-1-3二分法 HALF(A.B.EPS,F.X) 合 程序框图 A1=A B1=B FO=F(A) X=(A1+B1)/2 F=F(X) F=0 yes no no F0*F<0 yes A1=X B1=X no (B1-A1/X<EPS> yes 改进的二分法:将区间 [a,b]划分成若干小区间 RETURN
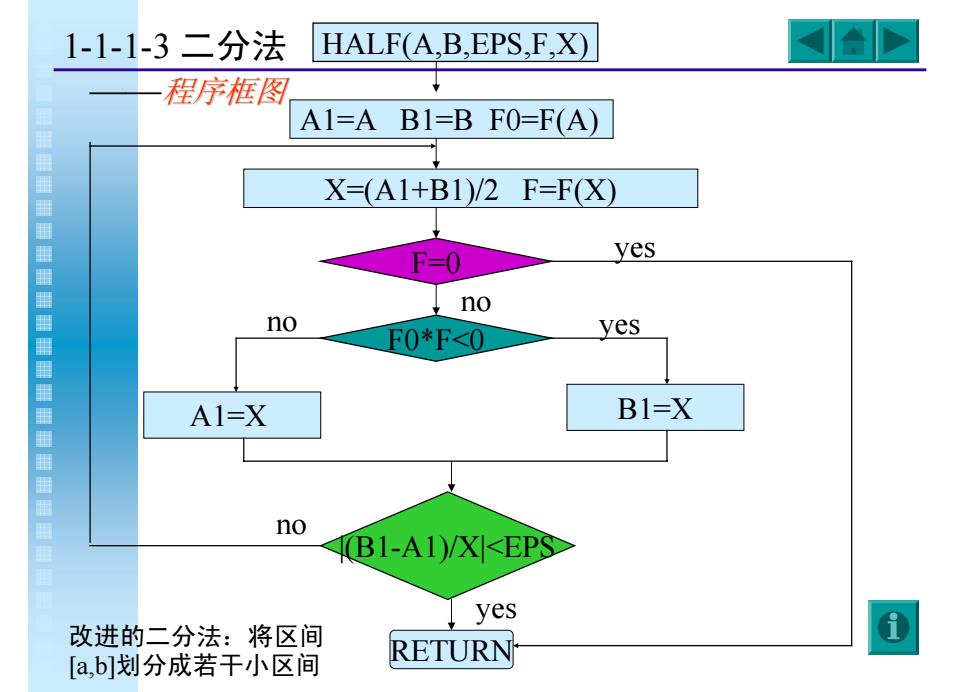
A1=A B1=B F0=F(A) X=(A1+B1)/2 F=F(X) A1=X RETURN HALF(A,B,EPS,F,X) F=0 F0*F<0 no B1=X |(B1-A1)/X|<EPS no yes yes yes no 改进的二分法:将区间 [a,b]划分成若干小区间 1-1-1-3 二分法 ——程序框图
1-1-1-4二分法 应用示例 开始 输入:M,N(①,K0,P 计算SR,SP,KN 定义函数SN,F=F(x) A=0.0B=1.0A1=AB1=BF1=F(A1)F2=F(B1) 调用二分法子程序求解方程F=0,解出转化率x 输出:转化率x 结束 显示程序
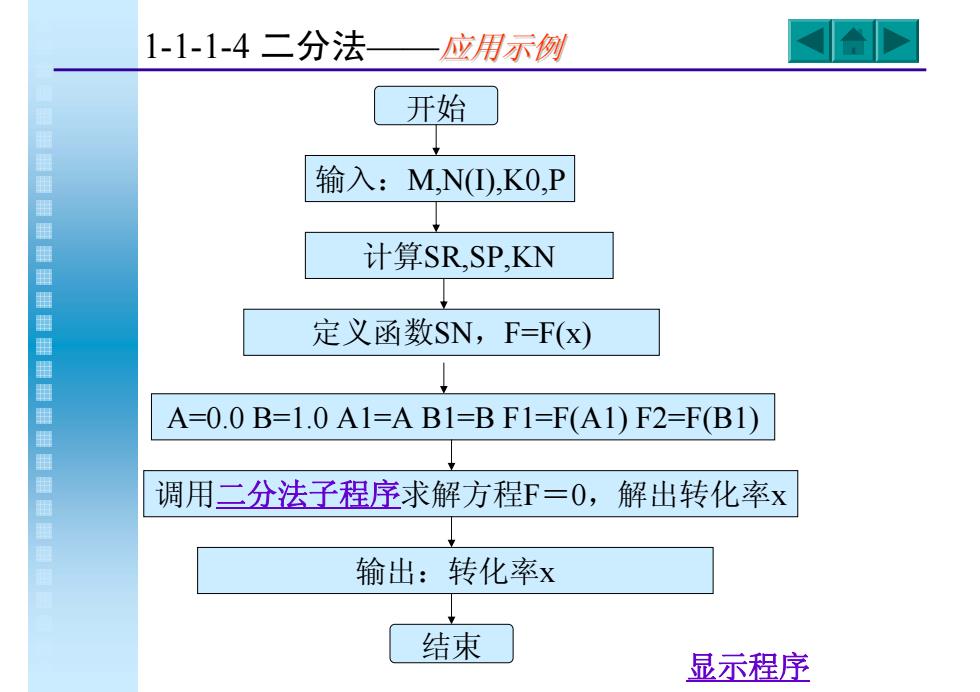
开始 输入:M,N(I),K0,P 计算SR,SP,KN A=0.0 B=1.0 A1=A B1=B F1=F(A1) F2=F(B1) 调用二分法子程序求解方程F=0,解出转化率x 输出:转化率x 结束 定义函数SN,F=F(x) 显示程序 1-1-1-4 二分法——应用示例
1-1-1-4二分法 应用示例 计算反应 )N(g)+H,(g=NH,(g 在773K时,不同压力一的平衡转化率,结果如 下:(已知773K时反应平衡常数0=0.3007) p/MPa 转化率x 0.1 0.986547 5.0 0.998097 10.0 0.998655 30.0 0.999223
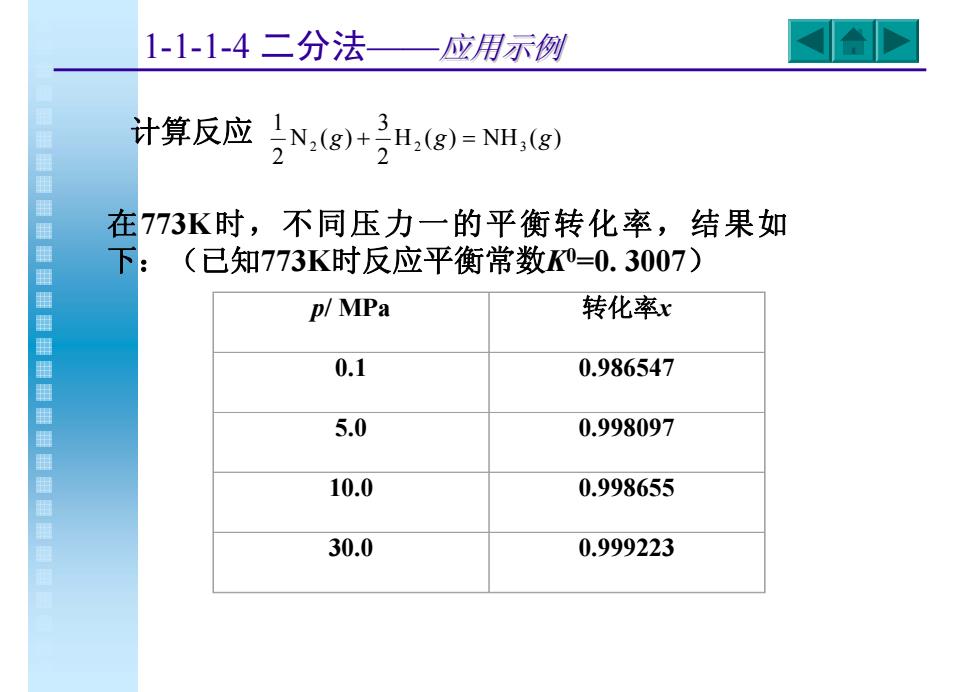
计算反应 H ( ) NH ( ) 23 N ( ) 21 2 g + 2 g = 3 g 在773K时,不同压力一的平衡转化率,结果如 下:(已知773K时反应平衡常数K0=0. 3007) p/ MPa 转化率x 0.1 0.986547 5.0 0.998097 10.0 0.998655 30.0 0.999223 1-1-1-4 二分法——应用示例

二分法一 练习 P48-6 弱酸及其相应共轭碱钠盐的水溶液平衡 回
二分法——练习 P48-6 弱酸及其相应共轭碱钠盐的水溶液平衡