
1.5传输矩阵与相空间、发射度和包络·刘 维尔定理 mi m2 01 612 M- m21 m22 012 22 以状态点坐标(r,P,)为方程变量,(rm,P,m)为束流质心 用矩阵Σ的益处是它的矩阵元即o1,o2和o2与粒子群性质联系密切 (U一Um)T∑1(U一Um)≤1πe就是该椭圆的面积e= /No1122- 2 012 或22(r-rm)2-2o2(r-rm)(P,-P,m)十1(P,-Pm)2≤e 011 n,3 2m1m12 m2 Um(动=MUm(a) 012 m121 1+2m42m1 m12n22 612 ←> Σ(=M()(M)I 022) 2 m21 m22 2 m22 022 3= 01 1 ,Q ,Y=型令R=Vo1为束流包络 7 刘维尔定理 相空间粒子集合体积在传输中不变
7
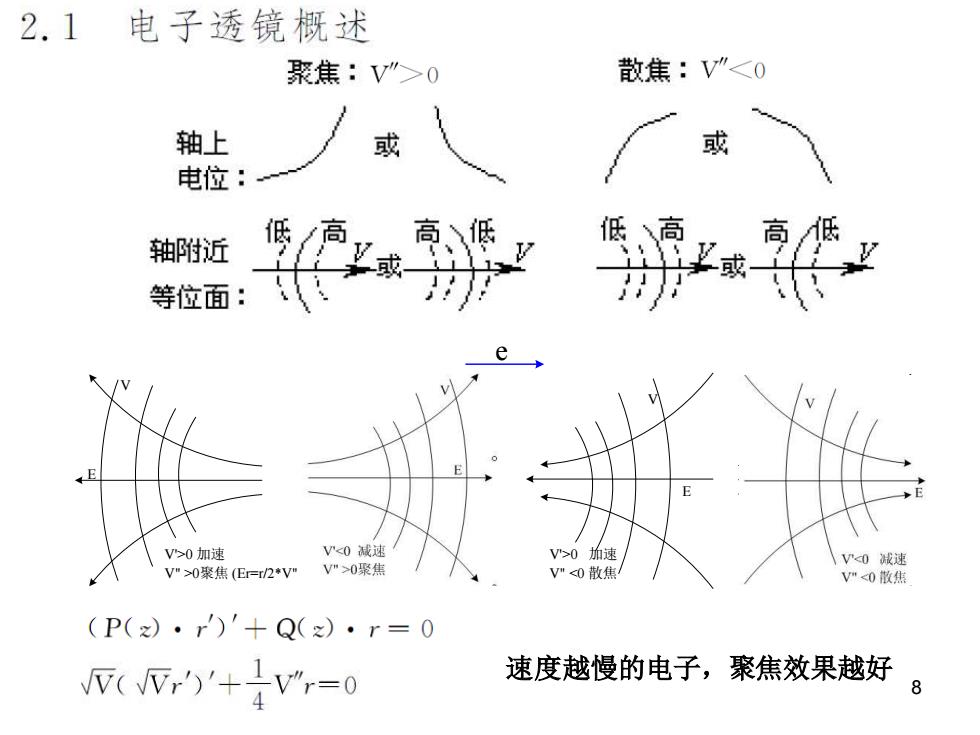
2.1 电子透镜概述 聚焦:V">0 散焦:V”<0 轴上 或 或 电位: 轴附近 局1 等位面: V>0加速 V<0减速 V">0加速 V0减速 V">0聚焦(E=r/2*V" V">0聚焦 V"<0散焦 V”0散焦 (P(z)·r)'+Q(x)·r=0 ()'+子=0 速度越慢的电子,聚焦效果越好
8 E V e V'>0 加速 V" >0聚焦 (Er=r/2*V") E V V'<0 减速 V" >0聚焦 E V V'<0 减速 V" <0 散焦 V'>0 加速 V" <0 散焦 E V 速度越慢的电子,聚焦效果越好
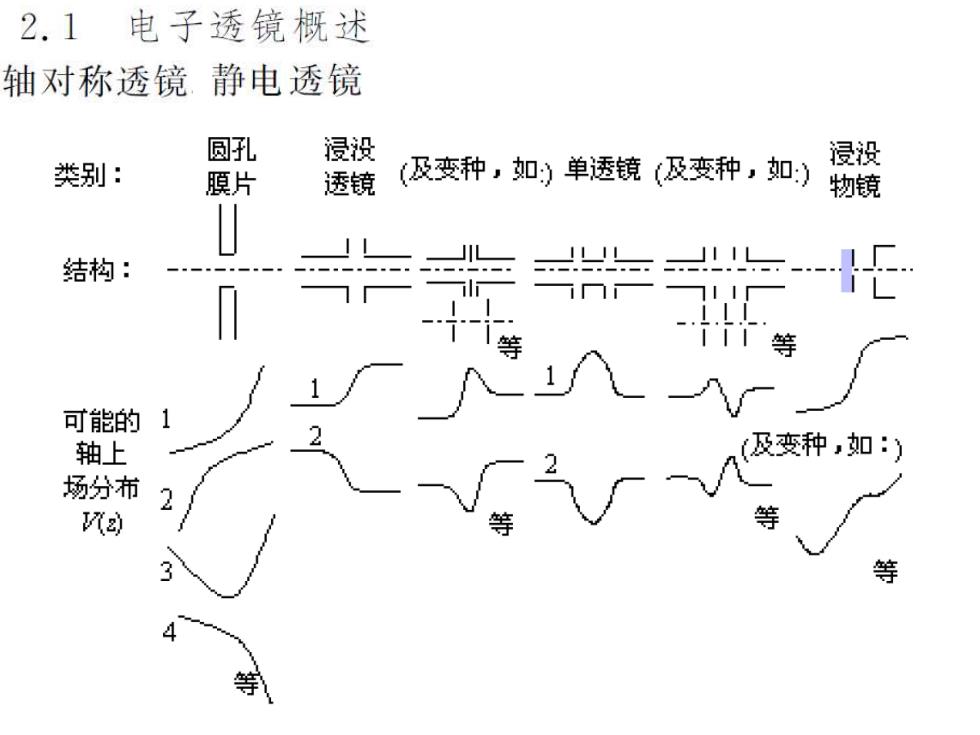
2.1电子透镜概述 轴对称透镜静电透镜 圆孔 浸没 类别: 膘片 透镜 (及变种,如)单透镜(及变种,如) 浸没 物镜 结构: 可能的 轴上 (及变种,如: 场分布 等 等 等
9
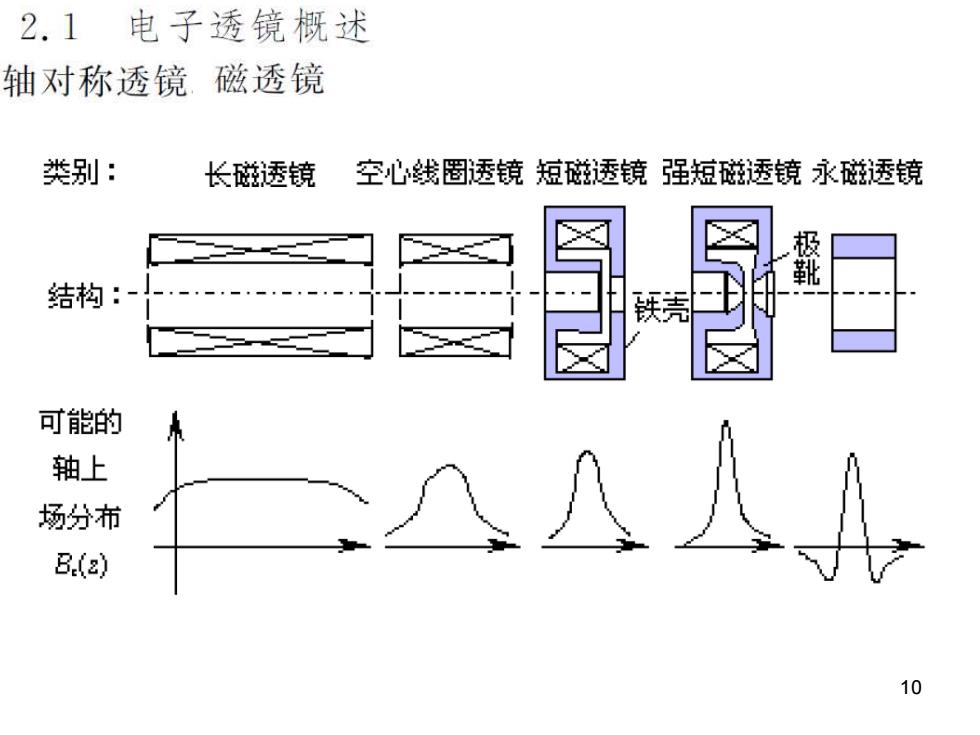
2.1 电子透镜概述 轴对称透镜磁透镜 类别: 长磁透镜 空心线圈透镜短磁透镜强短磁透镜永磁透镜 极 靴 结构: 可能的 轴上 场分布 B.( 10
10

2.2电子透镜的主要参量和传输矩阵、场分布 (P()·r)'+Q(z)·r=0 径向轨迹方程 ()'+V"+2Br=0 2m mii m2 薄透镜 厚透镜 m21 m22 m1= Qd之物方、像方焦距分别为f。=P。f,f=Pf 在电子光学中,对于静电透镜(B.=0),则有 六≈长:i=wf=W “简正焦距”F 在静电透镜中定义网数(R=V,F=Y 而对于磁透镜(设V=常数),则有 ≈Q=8 B.2dz 11 然后根据轴对称透镜的电磁场分布求的其焦距
11 然后根据轴对称透镜的电磁场分布求的其焦距