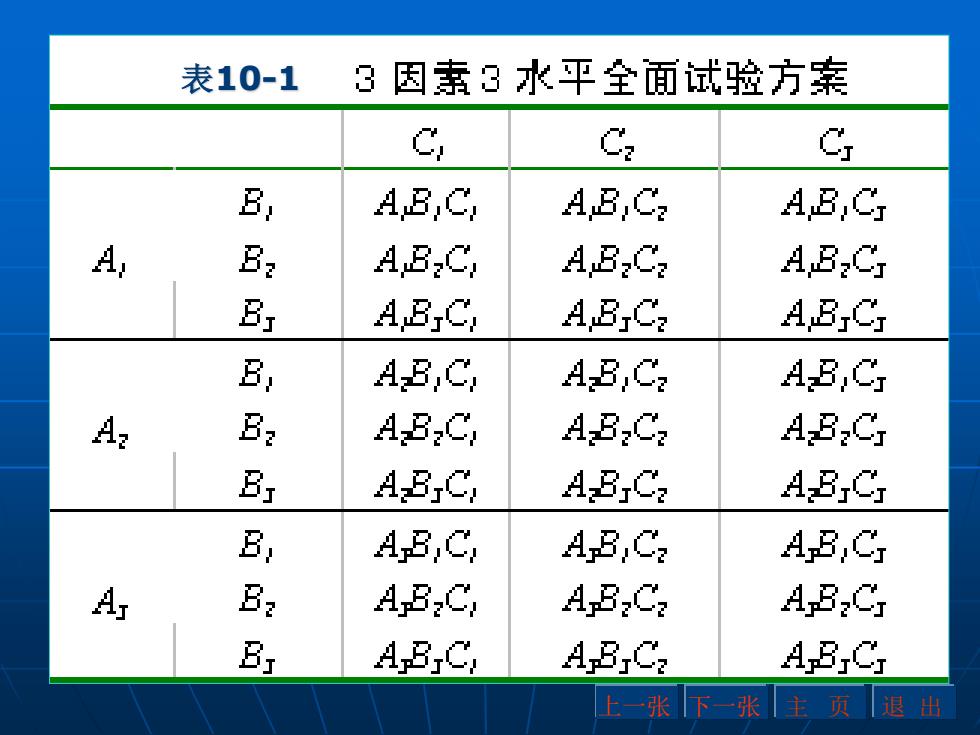
上一张 下一张 主 页 退 出 表10-1
上一张 下一张 主 页 退 出 表10-1
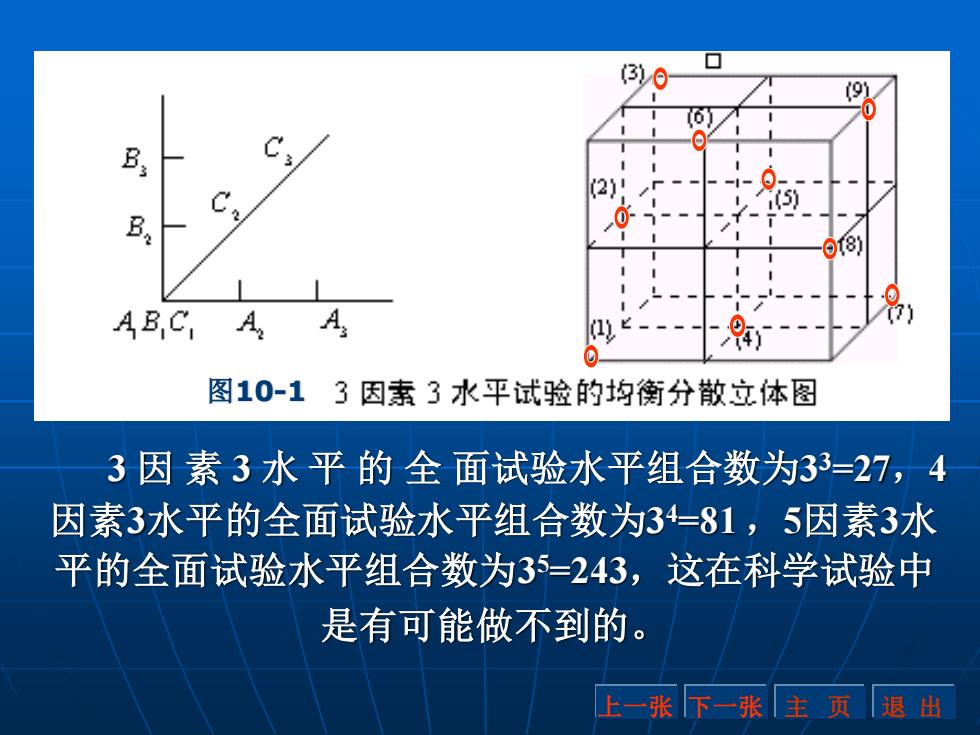
3 因 素 3 水 平 的 全 面试验水平组合数为3 3=27,4 因素3水平的全面试验水平组合数为3 4=81 ,5因素3水 平的全面试验水平组合数为3 5=243,这在科学试验中 是有可能做不到的。 上一张 下一张 主 页 退 出 图10-1
3 因 素 3 水 平 的 全 面试验水平组合数为3 3=27,4 因素3水平的全面试验水平组合数为3 4=81 ,5因素3水 平的全面试验水平组合数为3 5=243,这在科学试验中 是有可能做不到的。 上一张 下一张 主 页 退 出 图10-1

正交设计就是从选优区全面试验点(水平 组合)中挑选出有代表性的部分试验点(水平 组合)来进行试验。图10-1中标有试验号的九 个“(·)”,就是利用正交表L9 (3 4 )从27个试验点 中挑选出来的9个试验点。即: (1)A1B1C1 (2)A2B1C2 (3)A3B1C3 (4)A1B2C2 (5)A2B2C3 (6)A3B2C1 (7)A1B3C3 (8)A2B3C1 (9)A3B3C2 上一张 下一张 主 页 退 出
正交设计就是从选优区全面试验点(水平 组合)中挑选出有代表性的部分试验点(水平 组合)来进行试验。图10-1中标有试验号的九 个“(·)”,就是利用正交表L9 (3 4 )从27个试验点 中挑选出来的9个试验点。即: (1)A1B1C1 (2)A2B1C2 (3)A3B1C3 (4)A1B2C2 (5)A2B2C3 (6)A3B2C1 (7)A1B3C3 (8)A2B3C1 (9)A3B3C2 上一张 下一张 主 页 退 出

上述选择 ,保证了A因素的每个水平与B因素、C 因素的各个水平在试验中各搭配一次 。对于A、B、C 3个因素来说 , 是在27个全面试验点中选择9个试验 点 ,仅 是全面试验的 三分之一。 从图10-1中可以看到 ,9个试验点在选优区中分 布是均衡的,在立方体的每个平面上 ,都恰是3个试 验点;在立方体的每条线上也恰有一个试验点。 9个试验点均衡地分布于整个立方体内 ,有很强 的代表性 , 能 够比较全面地反映选优区内的基本情 况。 上一张 下一张 主 页 退 出
上述选择 ,保证了A因素的每个水平与B因素、C 因素的各个水平在试验中各搭配一次 。对于A、B、C 3个因素来说 , 是在27个全面试验点中选择9个试验 点 ,仅 是全面试验的 三分之一。 从图10-1中可以看到 ,9个试验点在选优区中分 布是均衡的,在立方体的每个平面上 ,都恰是3个试 验点;在立方体的每条线上也恰有一个试验点。 9个试验点均衡地分布于整个立方体内 ,有很强 的代表性 , 能 够比较全面地反映选优区内的基本情 况。 上一张 下一张 主 页 退 出

1.3 正交表及其基本性质 1.3.1 正交表 由于正交设计安排试验和分析试验结果都要用正 交表,因此,我们先对正交表作一介绍。 表10-2是一张正交表,记号为L8 (27 ),其中“L”代 表正交表;L右下角的数字“8”表示有8行 ,用这张正 交表安排试验包含8个处理(水平组合) ;括号内的底数 “2” 表示因素的水平数,括号内2的指数“7”表示有7 列 ,用这张正交表最多可以安排7个2水平因素。 上一张 下一张 主 页 退 出
1.3 正交表及其基本性质 1.3.1 正交表 由于正交设计安排试验和分析试验结果都要用正 交表,因此,我们先对正交表作一介绍。 表10-2是一张正交表,记号为L8 (27 ),其中“L”代 表正交表;L右下角的数字“8”表示有8行 ,用这张正 交表安排试验包含8个处理(水平组合) ;括号内的底数 “2” 表示因素的水平数,括号内2的指数“7”表示有7 列 ,用这张正交表最多可以安排7个2水平因素。 上一张 下一张 主 页 退 出