
二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 了解人类文明进步与文化发展的通识知识:系统了解计 知识整合 算机科学领域的各个分支、发展概况及其在社会发展中的重 课程学习目标1、2 要作用:系统掌握计算机科学、教育学的基本理论和基本方 法并具有一定的综合应用及实践能力。 掌握计算机科学基础理论、编程软件操作方法、办公软 教学能力 件操作方法以及信息教育技术,并获得较强的逻辑推理能力、 课程学习目标1、2、3 抽象思维能力和课程与教材的研究能力:具有熟练运用现代 计算机及信息教育技术进行教研的能力。 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章:矩阵及其应用(可支撑课程学习目标1、2、3) 1.教学目的和要求 了解矩阵理论的历史发展过程:掌握矩阵概念,熟悉矩阵运算:掌握可逆矩阵概念及判定:了解分 块矩阵概念及运算:掌握矩阵的初等变换及初等矩阵:了解矩阵在信息加密、人口流动等具体问题中的 应用。 2.教学内容 第11节:矩阵的概念 第12节:矩阵的运算 第1.3节:可逆矩阵 第1.4节:分块矩阵 第1.5节:矩阵的初等变换 第1.6节:初等矩阵 第1.7节:应用举例 3,重点:矩阵的运算:可逆矩阵的判定及可逆矩阵的求法:矩阵的初等变换。 4.难点:矩阵乘法运算:可逆矩阵的求法及应用:分块矩阵的运算。 5.课后习题:习题1(A),第1-22题。 6.学时:14学时 第二章行列式(可支撑课程学习目标1、2、3) 14
二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 知识整合 了解人类文明进步与文化发展的通识知识;系统了解计 算机科学领域的各个分支、发展概况及其在社会发展中的重 要作用;系统掌握计算机科学、教育学的基本理论和基本方 法并具有一定的综合应用及实践能力。 课程学习目标 1、2 教学能力 掌握计算机科学基础理论、编程软件操作方法、办公软 件操作方法以及信息教育技术,并获得较强的逻辑推理能力、 抽象思维能力和课程与教材的研究能力;具有熟练运用现代 计算机及信息教育技术进行教研的能力。 课程学习目标 1、2、3 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章:矩阵及其应用(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 了解矩阵理论的历史发展过程;掌握矩阵概念,熟悉矩阵运算;掌握可逆矩阵概念及判定;了解分 块矩阵概念及运算;掌握矩阵的初等变换及初等矩阵;了解矩阵在信息加密、人口流动等具体问题中的 应用。 2 . 教学内容 第 1.1 节:矩阵的概念 第 1.2 节:矩阵的运算 第 1.3 节:可逆矩阵 第 1.4 节:分块矩阵 第 1.5 节:矩阵的初等变换 第 1.6 节:初等矩阵 第 1.7 节:应用举例 3 . 重点:矩阵的运算;可逆矩阵的判定及可逆矩阵的求法;矩阵的初等变换。 4 . 难点:矩阵乘法运算;可逆矩阵的求法及应用;分块矩阵的运算。 5 . 课后习题:习题 1(A),第 1-22 题。 6 . 学时:14 学时 第二章 行列式(可支撑课程学习目标 1、2、3) 14

1.教学目的和要求 了解n阶行列式的概念:熟练掌握n阶行列式的性质及行列式按行(列)展开:掌握伴随矩阵概念 及简单应用。 2.教学内容 第2.1节:二阶、三阶行列式 第2.2节:n阶行列式的概念 第2.3节:行列式的性质 第2.4节:行列式按行(列)展开 第2.5节:行列式的应用 3.教学重点:利用行列式性质和按行(列)展开定理计算行列式。 4.教学难点:掌握行列式的计算方法和技巧。 5.课后习题:习题2(A),1-6题,9-12题,15题。 6.学时:10学时 第三章矩阵的秩与线性方程组(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握矩阵秩的概念和性质:掌握线性方程组的判定定理。 2.教学内容 第3.1节:矩阵的秩 第3.2节:线性方程组解的判定 第3.3节:分块矩阵的初等变换及其应用 第3.4节:应用举例 3.教学重点:矩阵秩的概念:线性方程组有解的判定定理。 4.教学难点:矩阵秩的性质及其应用:利用矩阵初等变换解线性方程组。 5.课后习题:习题3(A)1-7题。 6.学时:6学时 第四章向量空间(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握向量组线性相关性的判定:会求向量组的极大线性无关组及秩:了解维向量空间:了解向量 的内积与正交矩阵:熟练掌握线性方程组的求解方法和解的表达。 2.教学内容 第4.1节:n维向量 15
1 . 教学目的和要求 了解 n 阶行列式的概念;熟练掌握 n 阶行列式的性质及行列式按行(列)展开;掌握伴随矩阵概念 及简单应用。 2 . 教学内容 第 2.1 节:二阶、三阶行列式 第 2.2 节:n 阶行列式的概念 第 2.3 节:行列式的性质 第 2.4 节:行列式按行(列)展开 第 2.5 节:行列式的应用 3 . 教学重点:利用行列式性质和按行(列)展开定理计算行列式。 4 . 教学难点:掌握行列式的计算方法和技巧。 5 . 课后习题:习题 2(A),1-6 题,9-12 题,15 题。 6 . 学时:10 学时 第三章 矩阵的秩与线性方程组(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握矩阵秩的概念和性质;掌握线性方程组的判定定理。 2 . 教学内容 第 3.1 节:矩阵的秩 第 3.2 节:线性方程组解的判定 第 3.3 节:分块矩阵的初等变换及其应用 第 3.4 节:应用举例 3 . 教学重点:矩阵秩的概念;线性方程组有解的判定定理。 4 . 教学难点:矩阵秩的性质及其应用;利用矩阵初等变换解线性方程组。 5 . 课后习题:习题 3(A)1-7 题。 6 .学时:6 学时 第四章 向量空间(可支撑课程学习目标 1、2、3) 1 .教学目的和要求 掌握向量组线性相关性的判定;会求向量组的极大线性无关组及秩;了解 n 维向量空间;了解向量 的内积与正交矩阵;熟练掌握线性方程组的求解方法和解的表达。 2 .教学内容 第 4.1 节:n 维向量 15

第4.2节:向量组的线性相关性 第4.3节:向量组的秩 第4.4节:n维向量空间 第4.5节:向量的内积与正交矩阵 第4.6节:线性方程组解的结构 第4.7节:应用举例 3重点:向量组的线性相关性;向量组的极大线性无关组与秩:线性方程组解的结构。 4难点:向量组的线性相关性:线性方程组解的求解方法及解的结构。 5.课后习题:习题4(A)1-14题,25-32题,37-41题。 6.学时:18学时 第五章相似矩阵(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握方阵特征值和特征向量的计算方法:掌握相似矩阵的概念及判别方法:掌握实对称矩阵正交相 似于对角矩阵的方法:了解若尔当标准形。 2.教学内容 第5.1节:方阵的特征值与特征向量 第5.2节:相似矩阵 第5.3节:实对称矩阵的相似矩阵 第5.4节:若当标准形简介 第5.5节:应用举例 3.教学重点:方阵特征值和特征向量的求法:实对称矩阵正交相似于对角矩阵的方法。 4.教学难点:方阵特征值和特征向量的求法:实对称矩阵正交相似于对角矩阵的方法。 5.课后习题:习题5(A)1-17题。 6.学时:8学时 第六章二次型(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握二次型的矩阵表示:掌握化二次型为标准形的方法:掌握正定二次型和正定矩阵的判别方法。 2.教学内容 第6.1节:二次型及其矩阵表示 第6.2节:化二次型为标准形 第6.3节:正定二次型 16
第 4.2 节:向量组的线性相关性 第 4.3 节:向量组的秩 第 4.4 节:n 维向量空间 第 4.5 节:向量的内积与正交矩阵 第 4.6 节:线性方程组解的结构 第 4.7 节:应用举例 3 .重点: 向量组的线性相关性;向量组的极大线性无关组与秩;线性方程组解的结构。 4 .难点:向量组的线性相关性;线性方程组解的求解方法及解的结构。 5 . 课后习题:习题 4(A)1-14 题,25-32 题,37-41 题。 6 . 学时:18 学时 第五章 相似矩阵(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握方阵特征值和特征向量的计算方法;掌握相似矩阵的概念及判别方法;掌握实对称矩阵正交相 似于对角矩阵的方法;了解若尔当标准形。 2 .教学内容 第 5.1 节:方阵的特征值与特征向量 第 5.2 节:相似矩阵 第 5.3 节:实对称矩阵的相似矩阵 第 5.4 节:若当标准形简介 第 5.5 节:应用举例 3 . 教学重点:方阵特征值和特征向量的求法;实对称矩阵正交相似于对角矩阵的方法。 4 . 教学难点:方阵特征值和特征向量的求法;实对称矩阵正交相似于对角矩阵的方法。 5 . 课后习题: 习题 5(A)1-17 题。 6 . 学时:8 学时 第六章 二次型(可支撑课程学习目标 1、2、3) 1 .教学目的和要求 掌握二次型的矩阵表示;掌握化二次型为标准形的方法;掌握正定二次型和正定矩阵的判别方法。 2 .教学内容 第 6.1 节:二次型及其矩阵表示 第 6.2 节:化二次型为标准形 第 6.3 节:正定二次型 16

第6.4节:应用举例 3.教学重点:化二次型为标准形:正定二次型和正定矩阵的判别。 4.难点:化二次型为标准形:正定矩阵的判别。 5.课后习题:习题6(A)1-12题。 6.学时:8学时 (二)《线性代数》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标1 课程学习目标2 课程学习目标3 第1.1-1.7节 H H H 第2.1-2.5节 H L 第3.1-3.4节 H M 第4.14.7节 H L H 第5.1-5.5节 H H M 第6.1-6.4节 H M L (三)《线性代数》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 学习目标1:了解本课程的地位与作用。系统 1.讲授法。结合线性代数课程和学生学习的特点, 掌握本课程的基本概念、基本理论、基本方法 采用板书与多媒体结合的方式,利用启发式进行教 和简单应用。 学。注重线性代数基本概念、基本理论和基本方法 学习目标2:会利用矩阵等工具处理一些理论 的讲解:突出矩阵的思想和方法:利用矩阵理论解 问题,解决一些实际问题。 决一些实际问题:培养学生学科思维。 学习目标3:为后续课程的学习和学生的进一 步深造,打下坚实的基础。 2.练习法。通过大量习题演练,达到巩固知识, 学习目标2:会利用矩阵等工具处理一些理论 运用知识的目的:同时,掌握一些计算的技能和技 问题,解决一些实际问题。 巧:培养学生学习数学的兴趣。 3.自主学习法。让学生自主探究、思考难点和重点 学习目标3:为后续课程的学习和学生的进 以及课后习题(B),然后小组讨论,最后老师点评。 步深造,打下坚实的基础。 17
第 6.4 节:应用举例 3 . 教学重点:化二次型为标准形;正定二次型和正定矩阵的判别。 4 . 难点:化二次型为标准形;正定矩阵的判别。 5 .课后习题:习题 6(A)1-12 题。 6 .学时:8 学时 (二)《线性代数》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标 1 课程学习目标 2 课程学习目标 3 第 1.1-1.7 节 H H H 第 2.1-2.5 节 H L 第 3.1-3.4 节 H M 第 4.1-4.7 节 H L H 第 5.1-5.5 节 H H M 第 6.1-6.4 节 H M L (三)《线性代数》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 1. 讲授法。结合线性代数课程和学生学习的特点, 采用板书与多媒体结合的方式,利用启发式进行教 学。注重线性代数基本概念、基本理论和基本方法 的讲解;突出矩阵的思想和方法;利用矩阵理论解 决一些实际问题;培养学生学科思维。 学习目标 1:了解本课程的地位与作用。系统 掌握本课程的基本概念、基本理论、基本方法 和简单应用。 学习目标 2:会利用矩阵等工具处理一些理论 问题,解决一些实际问题。 学习目标 3:为后续课程的学习和学生的进一 步深造,打下坚实的基础。 2. 练习法。通过大量习题演练,达到巩固知识, 运用知识的目的;同时,掌握一些计算的技能和技 巧;培养学生学习数学的兴趣。 学习目标 2:会利用矩阵等工具处理一些理论 问题,解决一些实际问题。 3.自主学习法。让学生自主探究、思考难点和重点 以及课后习题(B),然后小组讨论,最后老师点评。 学习目标 3:为后续课程的学习和学生的进一 步深造,打下坚实的基础。 17
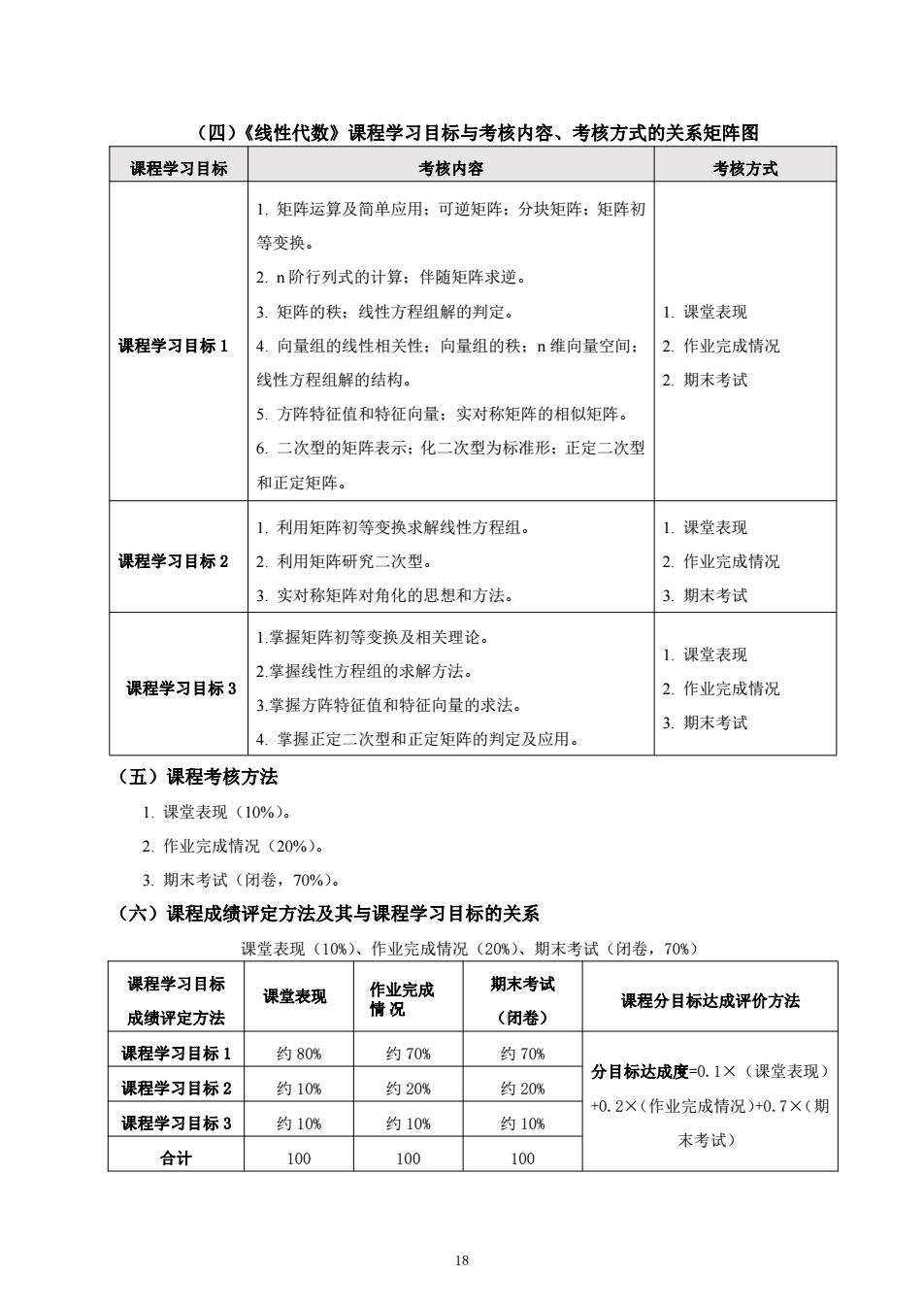
(四)《线性代数》课程学习目标与考核内容、考核方式的关系矩阵图 课程学习目标 考核内容 考核方式 1.矩阵运算及简单应用:可逆矩阵:分块矩阵:矩阵初 等变换。 2.n阶行列式的计算:伴随矩阵求逆。 3.矩阵的秩:线性方程组解的判定。 1. 课堂表现 课程学习目标1 4.向量组的线性相关性:向量组的秩:n维向量空间: 2.作业完成情况 线性方程组解的结构。 2.期末考试 5. 方阵特征值和特征向量;实对称矩阵的相似矩阵。 6.二次型的矩阵表示:化二次型为标准形:正定二次型 和正定矩阵。 1.利用矩阵初等变换求解线性方程组。 1. 课堂表现 课程学习目标2 2.利用矩阵研究二次型。 2.作业完成情况 3.实对称矩阵对角化的思想和方法。 3.期末考试 1.掌握矩阵初等变换及相关理论。 1.课堂表现 2.掌握线性方程组的求解方法。 课程学习目标3 2.作业完成情况 3掌握方阵特征值和特征向量的求法。 3.期末考试 4.掌握正定二次型和正定矩阵的判定及应用。 (五)课程考核方法 1.课堂表现(10%)。 2.作业完成情况(20%)。 3.期末考试(闭卷,70%)。 (六)课程成绩评定方法及其与课程学习目标的关系 课堂表现(10%)、作业完成情况(20%)、期末考试(闭卷,70%) 课程学习目标 课堂表现 作业完成 期末考试 课程分目标达成评价方法 成绩评定方法 情况 (闭卷) 课程学习目标1 约80% 约70% 约70% 分目标达成度=0.1×(课堂表现) 课程学习目标2 约10% 约20% 约20% +0.2×(作业完成情况)+0.7×(期 课程学习目标3 约10% 约10% 约10% 末考试) 合计 100 100 100 18
(四)《线性代数》课程学习目标与考核内容、考核方式的关系矩阵图 课程学习目标 考核内容 考核方式 课程学习目标 1 1. 矩阵运算及简单应用;可逆矩阵;分块矩阵;矩阵初 等变换。 2. n 阶行列式的计算;伴随矩阵求逆。 3. 矩阵的秩;线性方程组解的判定。 4. 向量组的线性相关性;向量组的秩;n 维向量空间; 线性方程组解的结构。 5. 方阵特征值和特征向量;实对称矩阵的相似矩阵。 6. 二次型的矩阵表示;化二次型为标准形;正定二次型 和正定矩阵。 1. 课堂表现 2. 作业完成情况 2. 期末考试 课程学习目标 2 1. 利用矩阵初等变换求解线性方程组。 2. 利用矩阵研究二次型。 3. 实对称矩阵对角化的思想和方法。 1. 课堂表现 2. 作业完成情况 3. 期末考试 课程学习目标 3 1.掌握矩阵初等变换及相关理论。 2.掌握线性方程组的求解方法。 3.掌握方阵特征值和特征向量的求法。 4. 掌握正定二次型和正定矩阵的判定及应用。 1. 课堂表现 2. 作业完成情况 3. 期末考试 (五)课程考核方法 1. 课堂表现(10%)。 2. 作业完成情况(20%)。 3. 期末考试(闭卷,70%)。 (六)课程成绩评定方法及其与课程学习目标的关系 课堂表现(10%)、作业完成情况(20%)、期末考试(闭卷,70%) 课程学习目标 成绩评定方法 课堂表现 作业完成 情 况 期末考试 (闭卷) 课程分目标达成评价方法 课程学习目标 1 约 80% 约 70% 约 70% 分目标达成度=0.1×(课堂表现) +0.2×(作业完成情况)+0.7×(期 末考试) 课程学习目标 2 约 10% 约 20% 约 20% 课程学习目标 3 约 10% 约 10% 约 10% 合计 100 100 100 18