
第2.6节:函数的性态与图形 第2.7节:微分学的实际应用 3.重点:导数的定义,函数的求导法则及函数的微分,微分中值定理,洛必达法则,泰勒公式,函数的 单调性与凹凸性,函数的极值与最值: 4.难点:复合函数的求导法则,反函数及参数方程求高阶导数,微分中值定理及其应用,函数图形的描 绘。 5.参考习题: 习题2-1:第1题、第3、4、6、8-11题 习题2-2:第1、2、3(5、6、11、13-16)、4(14-18)、5(11-18)、6、7(7-10)、8-19题 习题2-3:第1、5、6、8-10题 习题2-4:第1-10题 习题2-5:第1-4题 习题2-6:第1(4、7、8)、2-7、9-14、16题 习题2-7:第1-25题 章节测试题:全部 6.学时:24学时 第三章一元函数积分学及其应用(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握不定积分的概念与性质,求不定积分的方法与技巧,定积分概念与性质,微积分基本公式,求 定积分的方法与技巧,定积分的应用,反常定积的基本概念及计算。 2.教学内容 第3.1节:不定积分的概念与性质 第3.2节:不定积分的换元法与分部法 第33节:有理函数的不定积分 第3.4节:定积分的概念与性质 第3.5节:微积分基本定理 第3.6节:定积分的换元法与分部法 第3.7节:定积分的几何应用与物理应用 第3.8节:反常积分 3.重点:不定积分的概念与性质,不定积分的换元法与分部积分法,有理函数的积分:定积分的概念与 性质,微积分基本公式,定积分的换元积分与分部积分法:定积分微元法的思想,定积分在几何与物理 学方面的应用。 4.难点:利用第二换元积分法求不定积分,有理函数的不定积分:利用换元法求定积分:掌握微元法的
第 2.6 节:函数的性态与图形 第 2.7 节:微分学的实际应用 3.重点:导数的定义,函数的求导法则及函数的微分, 微分中值定理,洛必达法则,泰勒公式,函数的 单调性与凹凸性,函数的极值与最值; 4.难点:复合函数的求导法则,反函数及参数方程求高阶导数,微分中值定理及其应用,函数图形的描 绘。 5. 参考习题: 习题 2-1:第 1 题、第 3、4、6、8-11 题 习题 2-2:第 1、2、3(5、6、11、13-16)、4(14-18)、5(11-18)、6、7(7-10)、8-19 题 习题 2-3:第 1、5、6、8-10 题 习题 2-4:第 1-10 题 习题 2-5:第 1-4 题 习题 2-6:第 1(4、7、8)、2-7、9-14、16 题 习题 2-7:第 1-25 题 章节测试题:全部 6 . 学时:24 学时 第三章 一元函数积分学及其应用(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握不定积分的概念与性质,求不定积分的方法与技巧,定积分概念与性质,微积分基本公式,求 定积分的方法与技巧,定积分的应用,反常定积的基本概念及计算。 2 . 教学内容 第 3.1 节:不定积分的概念与性质 第 3.2 节:不定积分的换元法与分部法 第 3.3 节:有理函数的不定积分 第 3.4 节:定积分的概念与性质 第 3.5 节:微积分基本定理 第 3.6 节:定积分的换元法与分部法 第 3.7 节:定积分的几何应用与物理应用 第 3.8 节:反常积分 3.重点:不定积分的概念与性质,不定积分的换元法与分部积分法,有理函数的积分;定积分的概念与 性质,微积分基本公式,定积分的换元积分与分部积分法;定积分微元法的思想,定积分在几何与物理 学方面的应用。 4.难点:利用第二换元积分法求不定积分,有理函数的不定积分;利用换元法求定积分;掌握微元法的 4

思想及微元法的应用。 5.参考习题: 习题3-1:第2(11、13、14、18-26)、3-7题 习题3-2:第2-6题 习题3-3:第1-3题 习题3-4:第1(2)、3、3、6-9题 习题3-5:第1-13题 习题3-6:第1-11题 习题3-7:第1-8题 习题3-8:第1-3题 章节测试题:全部 6.学时:22学时 第四章微分方程(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握微分方程的基本概念,可分离变量的微分方程,齐次方程,一阶线性微分方程,可降阶的二阶 微分方程,线性微分方程解的结构,常系数齐次线性微分方程,常系数非齐次线性微分方程。 2.教学内容 第4.1节:微分方程的概念 第4.2节:一阶微分方程 第4.3节:二阶微分方程 3.重点:一阶线性微分方程,高阶线性微分方程,常系数非齐次线性微分方程: 4,难点:可降阶的高阶微分方程,常系数非齐次线性微分方程中特解的求法。 5.参考习题: 习题4-1:第1、2、5-7题 习题4-2:第1-3、5-8题 习题4-3:第1、4-6、8-9题 章节测试题:1、2、4-6 6.学时:12学时 第五章向量与空间解析几何(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握向量及其线性运算,数量积、向量积混合积,平面及其方程,空间直线及其方程,曲面及其 方程,空间曲线及其方程
思想及微元法的应用。 5 . 参考习题: 习题 3-1:第 2(11、13、14、18-26)、3-7 题 习题 3-2:第 2-6 题 习题 3-3:第 1-3 题 习题 3-4:第 1(2)、3、3、6-9 题 习题 3-5:第 1-13 题 习题 3-6:第 1-11 题 习题 3-7:第 1-8 题 习题 3-8:第 1-3 题 章节测试题:全部 6 . 学时:22 学时 第四章 微分方程(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握微分方程的基本概念,可分离变量的微分方程,齐次方程,一阶线性微分方程,可降阶的二阶 微分方程,线性微分方程解的结构,常系数齐次线性微分方程,常系数非齐次线性微分方程。 2 . 教学内容 第 4.1 节:微分方程的概念 第 4.2 节:一阶微分方程 第 4.3 节:二阶微分方程 3.重点:一阶线性微分方程,高阶线性微分方程,常系数非齐次线性微分方程; 4. 难点:可降阶的高阶微分方程,常系数非齐次线性微分方程中特解的求法。 5 . 参考习题: 习题 4-1:第 1、2、5-7 题 习题 4-2:第 1-3、5-8 题 习题 4-3:第 1、4-6、8-9 题 章节测试题:1、2、4-6 6 . 学时:12 学时 第五章 向量与空间解析几何(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握向量及其线性运算,数量积、向量积 混合积,平面及其方程,空间直线及其方程,曲面及其 方程,空间曲线及其方程。 5

2.教学内容 第5.1节:向量及其运算 第5.2节:平面及其方程 第5.3节:直线及其方程 第5.4节:曲面与曲线 3.重点:向量的数量积,向量积与混合积,曲面及其方程,曲线及其方程,平面及其方程,空间直线及 其方程: 4.难点:曲面及其方程,空间曲线及其方程,空间直线方程的求法。 5.参考习题: 习题5-1:第1-30题 习题5-2:第1、3-16题 习题5-3:第1-21题 习题5-4:第1-17题 章节测试题:全部 6.学时:14学时 第六章多元函数微分学(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握二元函数的概念、极限与连续,偏导数,全微分,多元复合函数的求导法则,隐函数的求导公 式,多元函数微分学的几何应用,方向导数与梯度,多元函数的极值及其求法。 2.教学内容 第6.1节:多元函数的概念、极限与连续 第6.2节:多元函数的偏导数与全微分 第63节:复合求导、隐函数的求导及方向导数 第6.4节:多元函数微分学的应用 3.重点:多元函数的偏导数,全微分,复合函数的求导法则,隐函数的求导公式,多元函数微分学在 几何方面的应用,多元函数的极值及其求法: 4.难点:复合函数的高阶导数求法,隐函数的求导公式的推导,多元函数的极值及求法。 5.参考习题: 习题6-1:第1-6题 习题6-2:第1-14题 习题6-3:第1-40题 习题6-4:第1-25题 6
2 . 教学内容 第 5.1 节:向量及其运算 第 5.2 节:平面及其方程 第 5.3 节:直线及其方程 第 5.4 节:曲面与曲线 3.重点:向量的数量积,向量积与混合积,曲面及其方程,曲线及其方程,平面及其方程,空间直线及 其方程; 4.难点:曲面及其方程,空间曲线及其方程,空间直线方程的求法。 5 . 参考习题: 习题 5-1:第 1-30 题 习题 5-2:第 1、3-16 题 习题 5-3:第 1-21 题 习题 5-4:第 1-17 题 章节测试题:全部 6 . 学时:14 学时 第六章 多元函数微分学(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握二元函数的概念、极限与连续,偏导数,全微分,多元复合函数的求导法则,隐函数的求导公 式,多元函数微分学的几何应用,方向导数与梯度,多元函数的极值及其求法。 2 . 教学内容 第 6.1 节:多元函数的概念、极限与连续 第 6.2 节:多元函数的偏导数与全微分 第 6.3 节:复合求导、隐函数的求导及方向导数 第 6.4 节:多元函数微分学的应用 3.重点:多元函数的偏导数,全微分,复合函数的求导法则,隐函数的求导公式,多元函数微分学在 几何方面的应用,多元函数的极值及其求法; 4. 难点:复合函数的高阶导数求法,隐函数的求导公式的推导,多元函数的极值及求法。 5 . 参考习题: 习题 6-1:第 1-6 题 习题 6-2:第 1-14 题 习题 6-3:第 1-40 题 习题 6-4:第 1-25 题 6

章节测试题:全部 6.学时:20学时 第七章多元函数积分学(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握二重积分的概念与性质,二重积分的计算法及应用,三重积分概念、计算和应用:对弧长的曲 线积分,对坐标的曲线积分,对面积的曲面积分,对坐标的曲面积分:格林公式及其应用,高斯公式通 量与散度,斯托克斯公式环流量与旋度。 2.教学内容 第7.1节:二重积分的概念、计算和应用 第72节:三重积分的概念、计算和应用 第7.3节:对弧长的曲线积分与对坐标的曲线积分 第7.4节:对面积的曲面积分与对坐标的曲面积分 第7.5节:格林公式、高斯高斯和斯托克斯公式 3.重点:二重积分的概念与性质,二重积分的计算,三重积分的计算,重积分的应用:重点是对弧长的 曲线积分,对坐标的曲线积分,格林公式及其应用,对面积的曲面积分,对坐标的曲面积分,高斯公式, 斯托克斯公式。 4.难点:在极坐标系下计算二重积分,三重积分的计算:对坐标的曲线与曲面积分,格林公式,高斯公 式,斯托克斯公式的条件,证明思想及其应用。 5.参考习题: 习题7-1:第1-31题 习题7-2:第1-13题 习题7-3:第1-13题 习题7-4:第1-8题 习题7-5:第1-16题 章节测试题:全部 6.学时:34学时 第八章无穷级数(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握常数项级数的概念和性质,常数项级数的审敛法,幂级数,函数展开成幂级数,函数的幂级数 展开式的应用,傅里叶级数,一般周期函数的傅里叶级数。 2.教学内容 第81节:常数项级数的概念与性质
章节测试题:全部 6 . 学时:20 学时 第七章 多元函数积分学(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握二重积分的概念与性质,二重积分的计算法及应用,三重积分概念、计算和应用;对弧长的曲 线积分,对坐标的曲线积分,对面积的曲面积分,对坐标的曲面积分;格林公式及其应用,高斯公式 通 量与散度,斯托克斯公式 环流量与旋度。 2 . 教学内容 第 7.1 节:二重积分的概念、计算和应用 第 7.2 节:三重积分的概念、计算和应用 第 7.3 节:对弧长的曲线积分与对坐标的曲线积分 第 7.4 节:对面积的曲面积分与对坐标的曲面积分 第 7.5 节:格林公式、高斯高斯和斯托克斯公式 3.重点:二重积分的概念与性质,二重积分的计算,三重积分的计算,重积分的应用;重点是对弧长的 曲线积分,对坐标的曲线积分,格林公式及其应用,对面积的曲面积分,对坐标的曲面积分,高斯公式, 斯托克斯公式。 4. 难点:在极坐标系下计算二重积分,三重积分的计算;对坐标的曲线与曲面积分,格林公式,高斯公 式,斯托克斯公式的条件,证明思想及其应用。 5 . 参考习题: 习题 7-1:第 1-31 题 习题 7-2:第 1-13 题 习题 7-3:第 1-13 题 习题 7-4:第 1-8 题 习题 7-5:第 1-16 题 章节测试题:全部 6 . 学时:34 学时 第八章 无穷级数(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握常数项级数的概念和性质,常数项级数的审敛法,幂级数,函数展开成幂级数,函数的幂级数 展开式的应用,傅里叶级数,一般周期函数的傅里叶级数。 2 . 教学内容 第 8.1 节:常数项级数的概念与性质 7
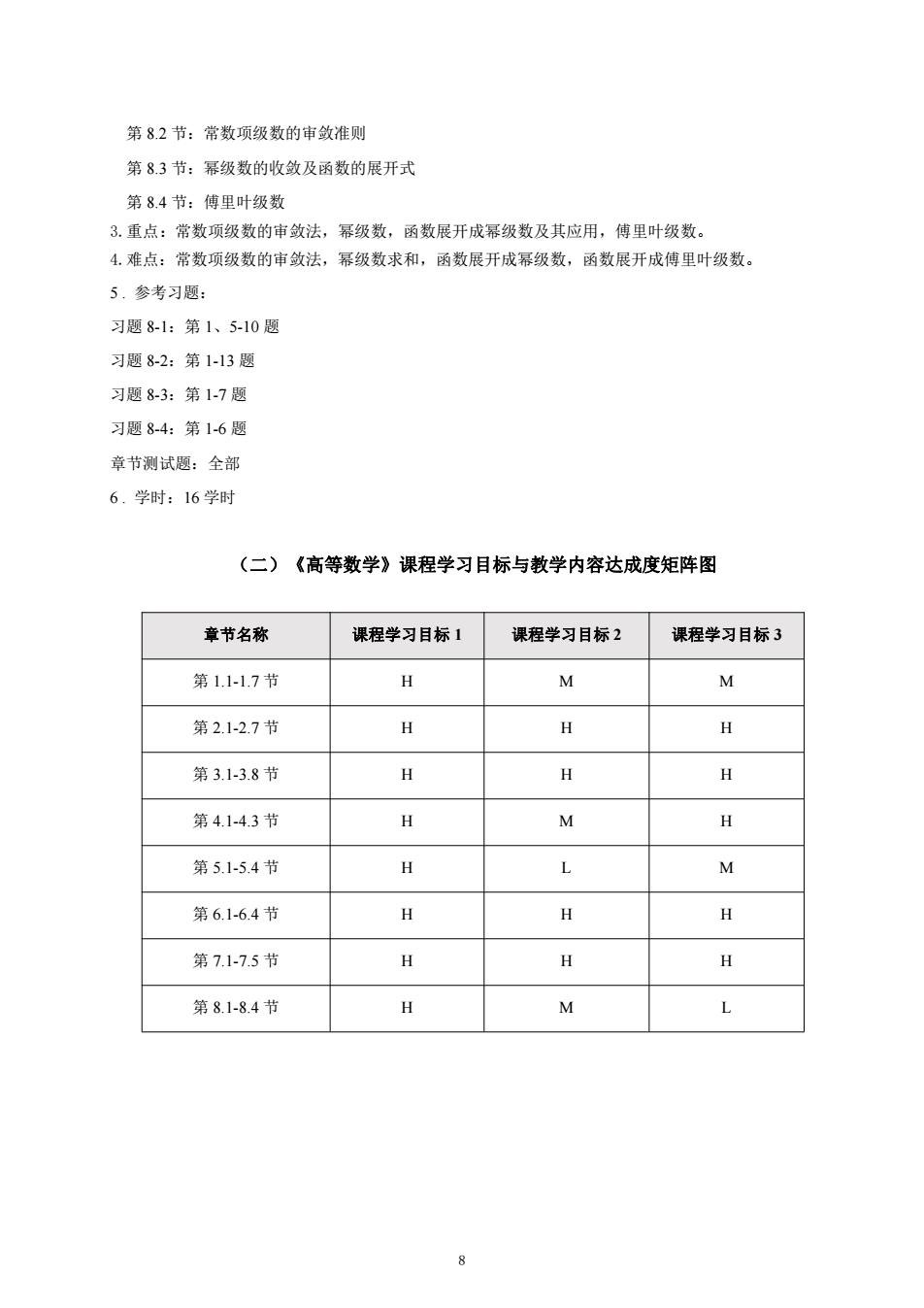
第8.2节:常数项级数的审敛准则 第8.3节:幂级数的收敛及函数的展开式 第8.4节:傅里叶级数 3.重点:常数项级数的审敛法,幂级数,函数展开成幂级数及其应用,傅里叶级数。 4.难点:常数项级数的审敛法,幂级数求和,函数展开成幂级数,函数展开成傅里叶级数。 5.参考习题: 习题8-1:第1、5-10题 习题8-2:第1-13题 习题8-3:第1-7题 习题8-4:第1-6题 章节测试题:全部 6.学时:16学时 (二) 《高等数学》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标1 课程学习目标2 课程学习目标3 第1.1-1.7节 H M M 第2.1-2.7节 H H H 第3.1-3.8节 H H H 第4.1-4.3节 H M H 第5.1-5.4节 H M 第6.1-6.4节 H H H 第7.1-7.5节 H H 夕 第8.1-8.4节 H M L
第 8.2 节:常数项级数的审敛准则 第 8.3 节:幂级数的收敛及函数的展开式 第 8.4 节:傅里叶级数 3.重点:常数项级数的审敛法,幂级数,函数展开成幂级数及其应用,傅里叶级数。 4.难点:常数项级数的审敛法,幂级数求和,函数展开成幂级数,函数展开成傅里叶级数。 5 . 参考习题: 习题 8-1:第 1、5-10 题 习题 8-2:第 1-13 题 习题 8-3:第 1-7 题 习题 8-4:第 1-6 题 章节测试题:全部 6 . 学时:16 学时 (二)《高等数学》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标 1 课程学习目标 2 课程学习目标 3 第 1.1-1.7 节 H M M 第 2.1-2.7 节 H H H 第 3.1-3.8 节 H H H 第 4.1-4.3 节 H M H 第 5.1-5.4 节 H L M 第 6.1-6.4 节 H H H 第 7.1-7.5 节 H H H 第 8.1-8.4 节 H M L 8