
大部分分离过程运行压力较低,可以当作理想气体的混合物 W =Tm [(ma mm)(Sia-S2a)+(mb /mm)(S18-S28)] Mm -[(mal mm)(hia-h2a)+(mb /mm)(hib-h26) pv =mRT e,nin P 理想气体混合物分离的理论功 h-h =cp(T2-T) W =Tm[(ma m)Ra (P/Pa)(m /mR(P)] Mm Pm mmRmTm /Vm mmRm 摩尔单位 Pm nm 1 T Pia maRaTa/Va maRa Pia 气体A的摩尔分量ya=na/nm 分离1摩尔混合物耗功为 =[.ln1/x,)+yn/%月 nm
大部分分离过程运行压力较低,可以当作理想气体的混合物 pv mRT 理想气体混合物分离的理论功 T Vm 摩尔单位 P P n n y m a m 1 a a 1 气体A的摩尔分量 分离1摩尔混合物耗功为 2 2 2 1 1 1 ln ln p T p s s c R T p 2 1 2 1 ( ) p h h c T T i m a a b b m - = ln(1/ ) ln(1/ ) W RT y y y y n

扩展到种组分理想气体混合物的完全分离 形=RI∑y,ln(1/y,) 混合物中j组分的摩尔分量 类似于定义液化系统的循环效率那样定义分离系统的分离效率FOM为 Wil nm -Wi/mm FOM= _Wnm -W mm
扩展到 j 种组分理想气体混合物的完全分离 混合物中 j 组分的摩尔分量 类似于定义液化系统的循环效率那样定义分离系统的分离效率FOM为 / / / / i m i m m m W n W m FOM W n W m i m m - = ln(1/ ) j j j W RT y y n
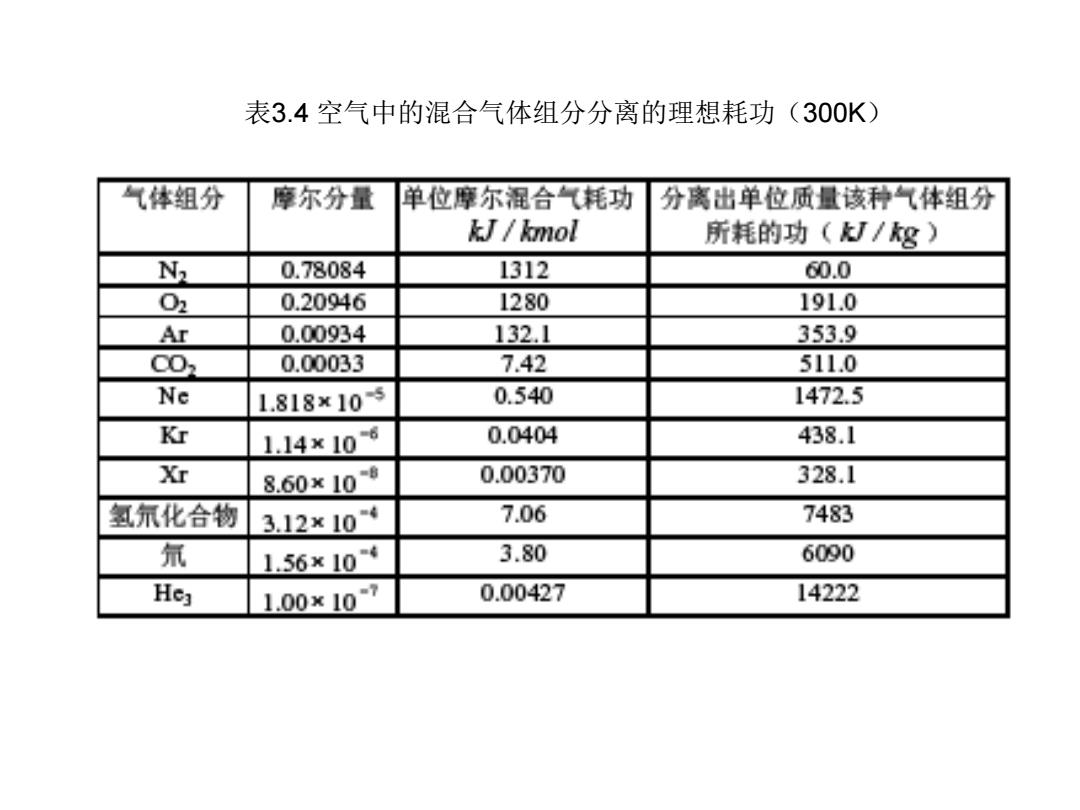
表3.4空气中的混合气体组分分离的理想耗功(300K) 气体组分 摩尔分量 单位摩尔混合气耗功 分离出单位质量该种气体组分 kJ/kmol 所耗的功(I/8) W 0.78084 1312 60.0 02 0.20946 1280 191.0 Ar 0.00934 132.1 353.9 C02 0.00033 7.42 511.0 Ne 1.818×105 0.540 1472.5 Kr 1.14×106 0.0404 438.1 Xr 8.60x108 0.00370 328.1 氢氘化合物 3.12×104 7.06 7483 氘 1.56×104 3.80 6090 He3 1.00×107 0.00427 14222
表3.4 空气中的混合气体组分分离的理想耗功(300K)
混合物的性质 (1)相律 单组分物质(例如氮气)单相 2个独立的热物性值(如温度和压力) 混合物单相 +摩尔百分比 单组份物质出现两相 只需一个物性参数(例如饱和温度) 多相多质 相律 T=C-P+2 体系状态所需独立变量数 组分数相数
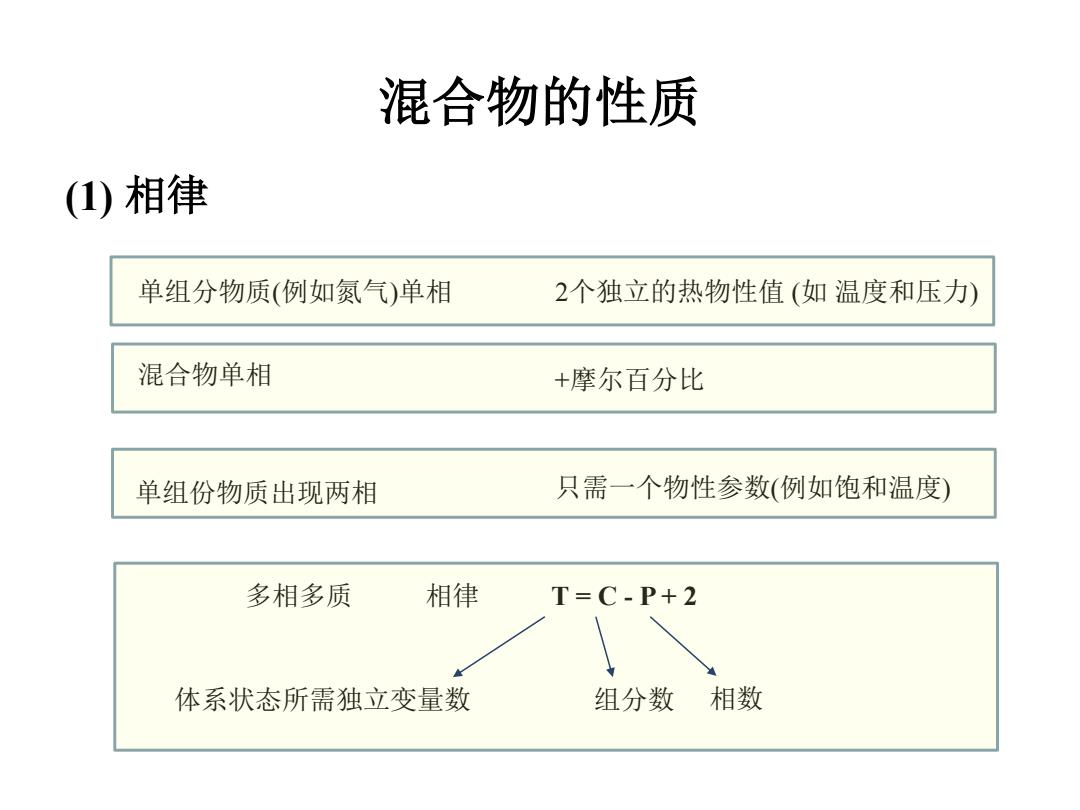
混合物的性质 (1) 相律 单组分物质(例如氮气)单相 2个独立的热物性值 (如 温度和压力) 混合物单相 +摩尔百分比 单组份物质出现两相 只需一个物性参数(例如饱和温度) 多相多质 相律 T = C - P + 2 体系状态所需独立变量数 组分数 相数
压力=常数 蒸气 双组分混合物相平衡曲线有几种可能出现的三种典型曲线 L+V 1.第一种:适用于压力低于双组分的临界压力, 液体 把空气看作是氦和氧的混合物时,压力在 (a) 摩尔百分比 100-1000kPa之间的液空属于这种情况。 蒸气 2.第二种:混合物中组分之一的临界压力低于 临界点 所作的温度-浓度图时的压力。氨~氦混合物 L+V 压力在2MPa左右会出现这种类型的曲线。 液体 3.第三种:在一定的浓度下混合物会转为共沸 (b) 摩尔百分比 混合物。这时混合物的性能与单纯组分物质 共沸点 完全一样。典型例子是在丙酮与三氟甲烷作 蒸气 为混合物会产生这种现象。用精馏原理无法 黄 L+V 把这类共沸混合物分开。幸好,低温流体在 分离时不会形成共沸混合物。 液体 0 摩尔百分比 (c)
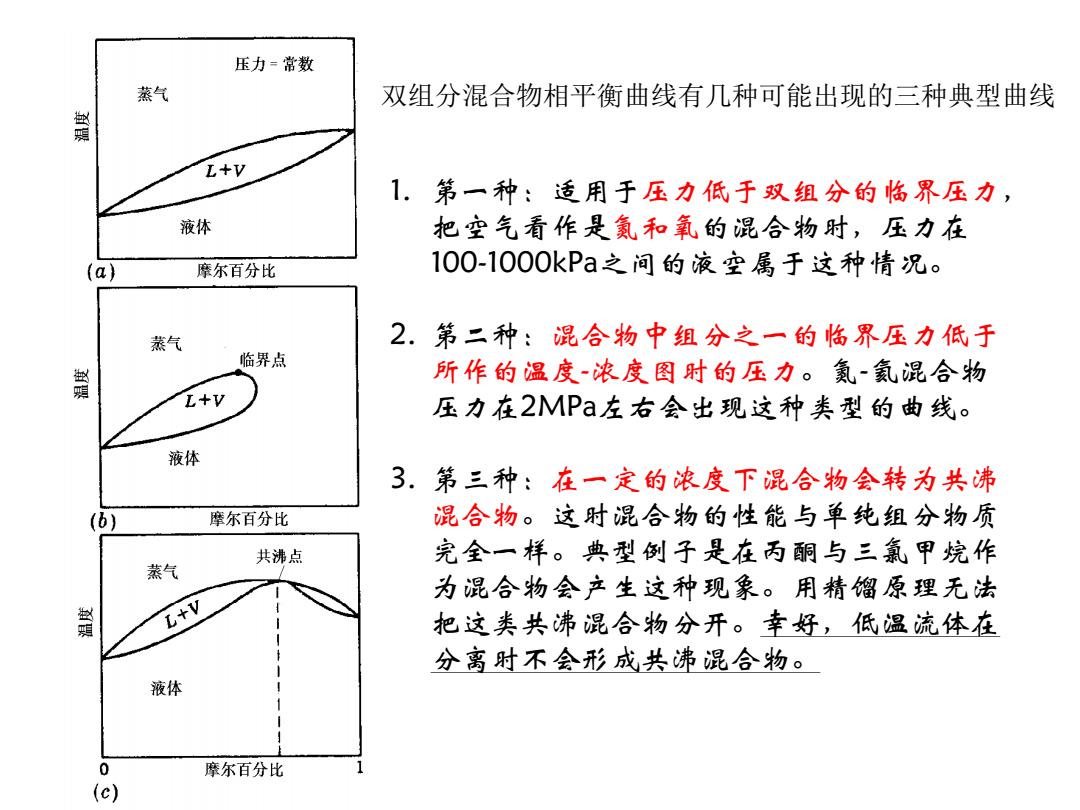
1. 第一种:适用于压力低于双组分的临界压力, 把空气看作是氮和氧的混合物时,压力在 100-1000kPa之间的液空属于这种情况。 2. 第二种:混合物中组分之一的临界压力低于 所作的温度-浓度图时的压力。氮-氦混合物 压力在2MPa左右会出现这种类型的曲线。 3. 第三种:在一定的浓度下混合物会转为共沸 混合物。这时混合物的性能与单纯组分物质 完全一样。典型例子是在丙酮与三氯甲烷作 为混合物会产生这种现象。用精馏原理无法 把这类共沸混合物分开。幸好,低温流体在 分离时不会形成共沸混合物。 双组分混合物相平衡曲线有几种可能出现的三种典型曲线