
第三章分组密码:3.1分组密码概述 3.1.4分组密码常用计算组件和结构 1.群加密:线性计算组件 逐比特异或⊕,结构最简单,缺点也最明显,密文的一个比特只 依赖于明文的一个比特和密钥的一个比特,毫无扩散功能。 (od2m加法“+”也是非常简单的计算组件,具有单向扩散功能, 即明文或密钥的第位影响密文的第位、第什1位、.、第位。 s2.置换(Permutation) 不改变明文比特,只打乱位置,以充分扩散。一般用置换表实现 ● 扩展置换:在置换的基础上,将某些bt重复出现,明文长度扩展 3.代换(Substitution):非线性组件 称明文分组到密文分组的可逆变换为代换 ·(与古典密码中代换表同义) ·如DEA使用的mod216+1乘法,具有非线性运算功能 ·AES中的字节替代 。DES中的S盒 历些毛子代枝大学 17/
3.1.4 分组密码常用计算组件和结构 1. 群加密:线性计算组件 ⚫ 逐比特异或,结构最简单,缺点也最明显,密文的一个比特只 依赖于明文的一个比特和密钥的一个比特,毫无扩散功能。 ⚫ (mod 2n )加法“+”也是非常简单的计算组件,具有单向扩散功能, 即明文或密钥的第j位影响密文的第j位、第j+1位、…、第n位。 2. 置换( Permutation ) ⚫ 不改变明文比特,只打乱位置,以充分扩散。一般用置换表实现 ⚫ 扩展置换:在置换的基础上,将某些bit重复出现,明文长度扩展 3. 代换( Substitution ):非线性组件 ⚫ 称明文分组到密文分组的可逆变换为代换 ⚫ (与古典密码中代换表同义) ⚫ 如IDEA使用的mod 216+1乘法,具有非线性运算功能 ⚫ AES中的字节替代 ⚫ DES中的S盒 17/ 第三章 分组密码:3.1 分组密码概述

第三章分组密码:3.1分组密码概述 3.1.4分组密码设计中的常用计算组件 即代换是输入集A到输出集合A'上的双射变换:f:A→A 式中,是控制输入变量,即密钥 0 密钥k决定了使用哪一个代换,是代换函数的一部分,k不同则 对应的代换(可逆映射)也不同,所以加密算法中的代换其代换结 构同,区别在于使用的密钥变量的不同 ·双射条件保证在给定下可从密文惟一恢复明文 。代换的数量 。如果明文和密文的分组长都为比特,则明文的每一个分组都有 2个可能的取值,则不同可逆变换的个数有2!个。2的全排列 。代换通常是高度非线性函数 1)用“解析表达式”,将自变量的值代入“解析表达式”,计 算出函数值。节省空间,但是太慢,一般很少用 2)将代换用输入输出真值表表达,计算即查表,速度快,经常 使用 历粤毛子神枝大学 18/
3.1.4 分组密码设计中的常用计算组件 ⚫ 即代换是输入集A到输出集合A上的双射变换: fk:A→A ⚫ 式中,k是控制输入变量,即密钥 ⚫ 密钥k决定了使用哪一个代换,是代换函数的一部分,k不同则 对应的代换(可逆映射)也不同,所以加密算法中的代换其代换结 构同,区别在于使用的密钥变量的不同 ⚫ 双射条件保证在给定k下可从密文惟一恢复明文 ⚫ 代换的数量 ⚫ 如果明文和密文的分组长都为n比特,则明文的每一个分组都有 2 n个可能的取值,则不同可逆变换的个数有2 n !个。2 n的全排列 ⚫ 代换通常是高度非线性函数 ⚫ 1)用“解析表达式”,将自变量的值代入“解析表达式”,计 算出函数值。节省空间,但是太慢,一般很少用 ⚫ 2)将代换用输入/输出真值表表达,计算即查表,速度快,经常 使用 18/ 第三章 分组密码:3.1 分组密码概述
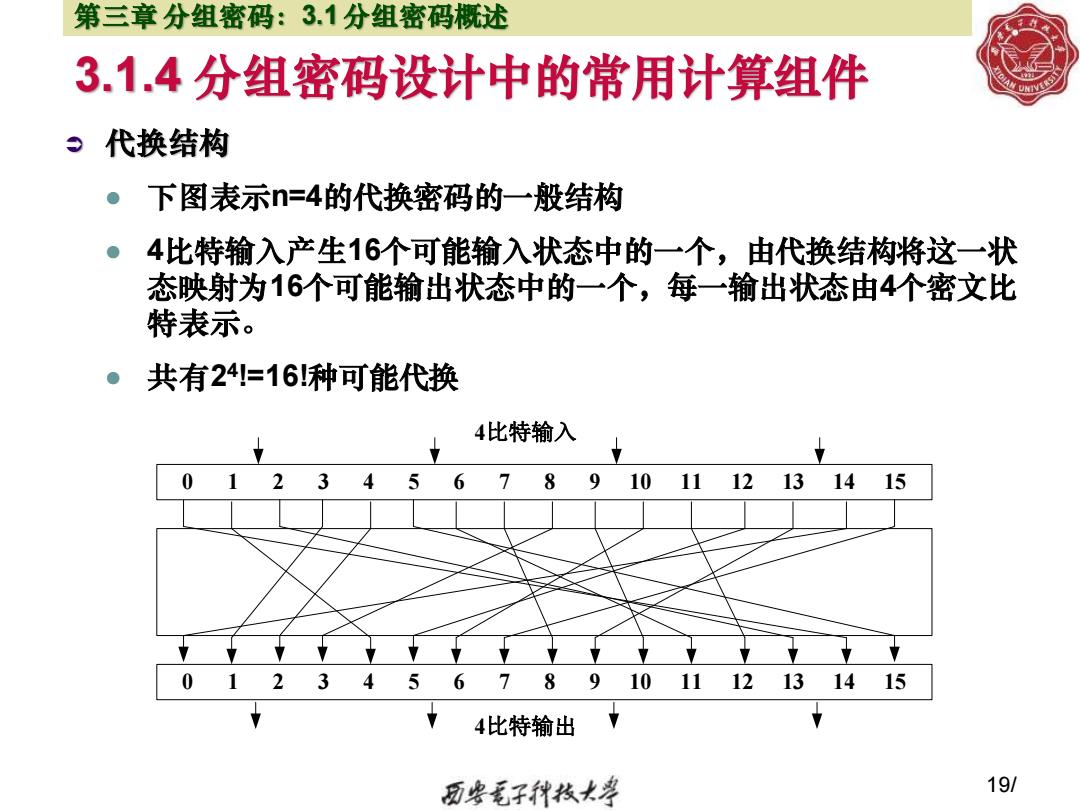
第三章分组密码:3.1分组密码概述 3.1.4分组密码设计中的常用计算组件 。代换结构 下图表示n=4的代换密码的一般结构 4比特输入产生16个可能输入状态中的一个,由代换结构将这一状 态映射为16个可能输出状态中的一个,每一输出状态由4个密文比 特表示。 。共有241=16种可能代换 4比特输入 0 1 2345 678910111213 1415 0 1 234 5 6 8 9 101112131415 4比特输出 粤毛子代枝大学 19/
3.1.4 分组密码设计中的常用计算组件 代换结构 ⚫ 下图表示n=4的代换密码的一般结构 ⚫ 4比特输入产生16个可能输入状态中的一个,由代换结构将这一状 态映射为16个可能输出状态中的一个,每一输出状态由4个密文比 特表示。 ⚫ 共有2 4 !=16!种可能代换 19/ 第三章 分组密码:3.1 分组密码概述 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 4比特输入 4比特输出
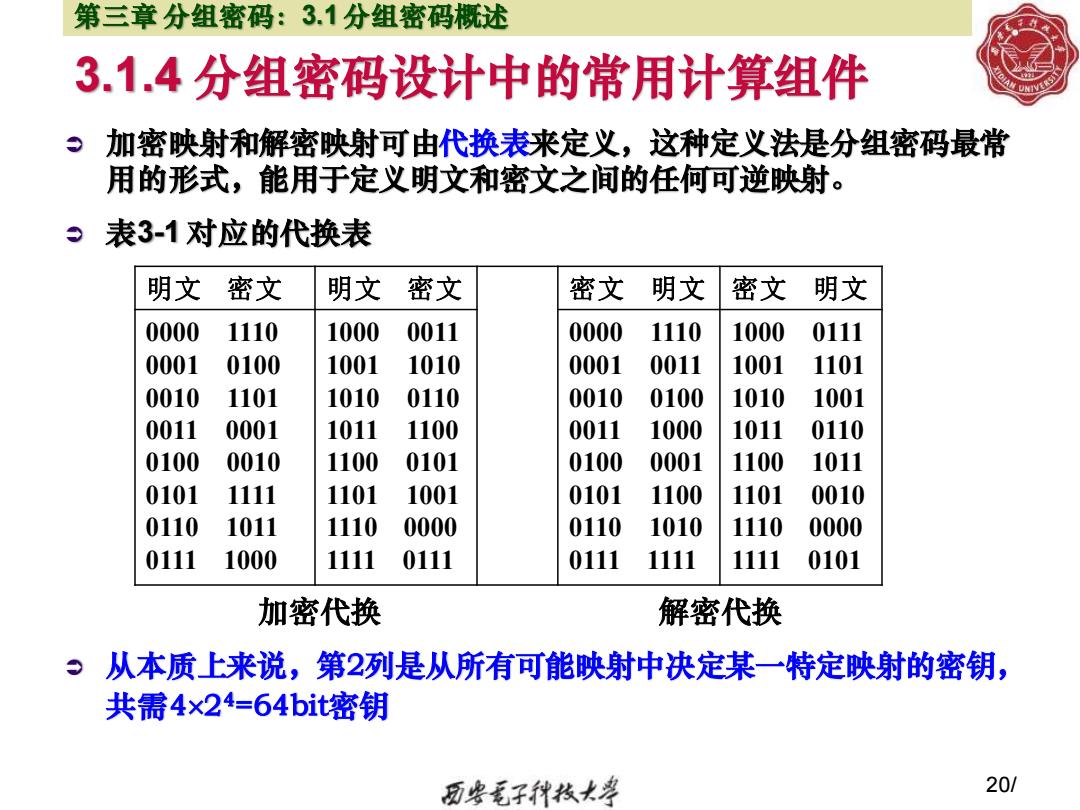
第三章分组密码:3.1分组密码概述 3.1.4分组密码设计中的常用计算组件 加密映射和解密映射可由代换表来定义,这种定义法是分组密码最常 用的形式,能用于定义明文和密文之间的任何可逆映射。 表3-1对应的代换表 明文 密文 明文 密文 密文 明文 密文 明文 0000 1110 1000 0011 0000 1110 1000 0111 0001 0100 1001 1010 0001 0011 1001 1101 0010 1101 1010 0110 0010 0100 1010 1001 0011 0001 1011 1100 0011 1000 1011 0110 0100 0010 1100 0101 0100 0001 1100 1011 0101 1111 1101 1001 0101 1100 1101 0010 0110 1011 1110 0000 0110 1010 1110 0000 0111 1000 1111 0111 0111 1111 1111 0101 加密代换 解密代换 9从本质上来说,第2列是从所有可能映射中决定某一特定映射的密钥, 共需4×24=64bit密钥 历粤毛子代牧大学 20/
3.1.4 分组密码设计中的常用计算组件 加密映射和解密映射可由代换表来定义,这种定义法是分组密码最常 用的形式,能用于定义明文和密文之间的任何可逆映射。 表3-1 对应的代换表 从本质上来说,第2列是从所有可能映射中决定某一特定映射的密钥, 共需424=64bit密钥 20/ 第三章 分组密码:3.1 分组密码概述 明文 密文 明文 密文 密文 明文 密文 明文 0000 1110 0001 0100 0010 1101 0011 0001 0100 0010 0101 1111 0110 1011 0111 1000 1000 0011 1001 1010 1010 0110 1011 1100 1100 0101 1101 1001 1110 0000 1111 0111 0000 1110 0001 0011 0010 0100 0011 1000 0100 0001 0101 1100 0110 1010 0111 1111 1000 0111 1001 1101 1010 1001 1011 0110 1100 1011 1101 0010 1110 0000 1111 0101 加密代换 解密代换

第三章分组密码:3.1分组密码概述 3.1.4分组密码设计中的常用计算组件 这种代换结构中分组长度不宜太小 如果分组长度太小,如=4,系统则等价于古典的代换密码,容易 通过对明文的统计分析而被攻破。 如果分组长度足够大,而且从明文到密文可有任意可逆的代换, 那么明文的统计特性将被隐藏而使以上的攻击不能奏效。 但代换结构中的分组长度也不宜很大 。会使代换表规模呈几何级数增加 由表3.1的情况可知,一般地,对比特的代换结构,密钥的大小是 n×2比特。 ●如对64比特的分组,密钥大小应是64×264=270≈1021比特,因此难 以处理。 。若可用一个由比特密钥确定的函数来描述映射,则密钥量就是n 历粤毛子代枝七学 21/
3.1.4 分组密码设计中的常用计算组件 这种代换结构中分组长度不宜太小 ⚫ 如果分组长度太小,如n=4,系统则等价于古典的代换密码,容易 通过对明文的统计分析而被攻破。 ⚫ 如果分组长度n足够大,而且从明文到密文可有任意可逆的代换, 那么明文的统计特性将被隐藏而使以上的攻击不能奏效。 但代换结构中的分组长度也不宜很大 ⚫ 会使代换表规模呈几何级数增加 ⚫ 由表3.1的情况可知,一般地,对n比特的代换结构,密钥的大小是 n×2 n比特。 ⚫ 如对64比特的分组,密钥大小应是64×2 64=270≈ 1021比特,因此难 以处理。 ⚫ 若可用一个由n比特密钥确定的函数来描述映射,则密钥量就是n 21/ 第三章 分组密码:3.1 分组密码概述