
9.电磁波 平面电磁波 E=Eo cos@ H=Ho cos@ au sE=H 能量密度 (EE2 uH2 能流密度 S=ExH
9.电磁波 平面电磁波 = − v r E E cos t 0 = − v r H H cos t 0 1 v = E = H 能量密度 ( ) 2 2 2 1 w = E + H 能流密度 S E H =
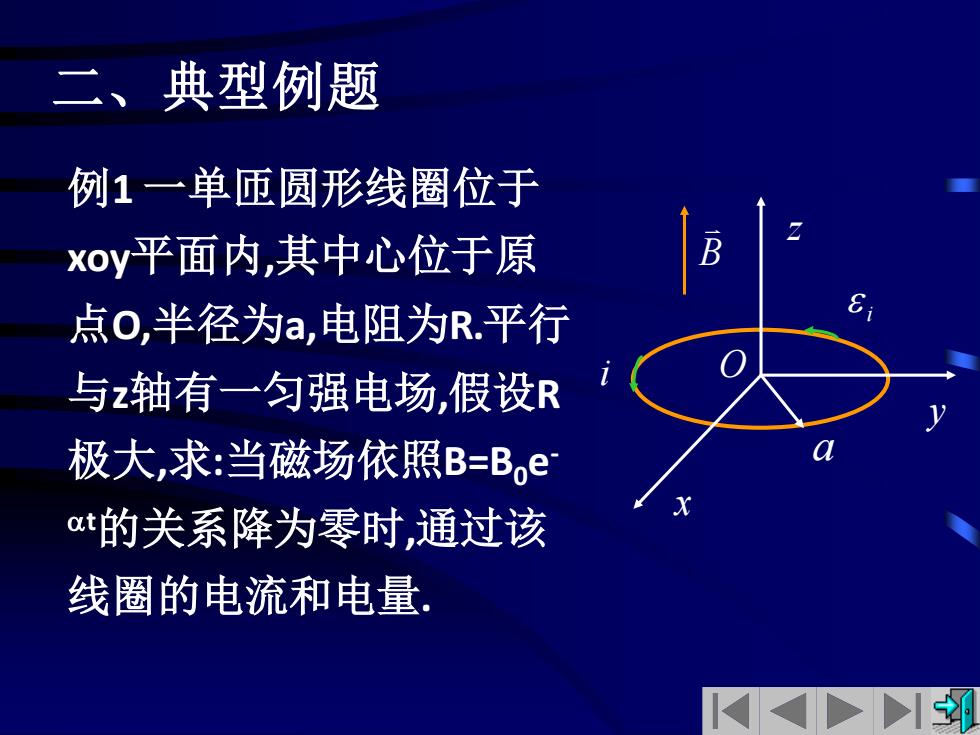
二、典型例题 例1一单匝圆形线圈位于 xoy平面内,其中心位于原 点o,半径为a,电阻为R平行 与z轴有一匀强电场,假设R 极大,求:当磁场依照B=Boe t的关系降为零时,通过该 线圈的电流和电量
例1 一单匝圆形线圈位于 xoy平面内,其中心位于原 点O,半径为a,电阻为R.平行 与z轴有一匀强电场,假设R 极大,求:当磁场依照B=B0e - t的关系降为零时,通过该 线圈的电流和电量. B z x y O i i a 二、典型例题

解:电路中维持电流的条件 是必须有电动势,求感应电 流应首先求出感应电动势. 题中线圈不动亦不变形,故 线圈内只存在感应电动势」 B变化时,伴有自感应现象,但题中假设很 大,自感应电流就极小,可以忽略
解: 电路中维持电流的条件 是必须有电动势,求感应电 流应首先求出感应电动势. 题中线圈不动亦不变形,故 线圈内只存在感应电动势. B变化时,伴有自感应现象,但题中假设R很 大,自感应电流就极小,可以忽略. B z x y O i i a

根据法拉第电磁感应定律线圈中的感应电动势 dΦ 8= dt =-SB(-a)e na'aBe 电动势为正,说明它的方向与B构成右手螺旋关系. 根据欧姆定律线圈中的感应电流为 =na'aB R R 感应电流的方向亦与B构成右手螺旋关系
根据法拉第电磁感应定律,线圈中的感应电动势 dt d m i = − (BS ) dt d = − ( ) t B e dt d S − = − 0 ( ) t SB e − = − 0 − t a B e − = 0 2 电动势为正,说明它的方向与B构成右手螺旋关系. 根据欧姆定律,线圈中的感应电流为 i t e R a B R i − = = 0 2 感应电流的方向亦与B构成右手螺旋关系

在0~t时间内,通过线圈某一截面的电量为 dt mB-e-.)》=4w. 当B降为零时,通过线圈截面的总电量为 R R 可见,q仅与磁通量的变化值△Φn有关,而 与变化过程无关,即与Bt无关
在0t时间内,通过线圈某一截面的电量为 e dt R a B q idt t t t − = = 0 0 0 2 ( ) t e R a B − = 1− 0 2 ( (t)) R = m0 − m 1 m R − = 1 当B降为零时,通过线圈截面的总电量为 R R a B q idt m0 0 0 2 = = = 可见,q仅与磁通量的变化值m有关,而 与变化过程无关,即与B(t)无关