
1、十进制数转换成二进制数 (N)2= Bm-12m-l+Bn-22m-2++B020+B.12-l+B22-2+.+B.m2-m 整数部分 ※ 小数部分 整数部分除以2:(B-2n-1+Bm-22m-2+.+B21+B20)/2 =(Bm-12-2+Bn-22-3++B120).B0 第一次商 余数 第-次商/2=(B-12n-3+Bn-22n-4+.+B220).B 第二次商 数 小数部分乘以2: (B.12-1+B22-2+.+B.m2-m)2 =B.1十(B.22-l+..+B.m2m+1) 整数 第一次小数 第-次小数×2=B.2十(B.321+.+B.m2-m+2) 整数 第二次小数
1、十进制数转换成二进制数 (N)2= Bn-12 n-1+Bn-22 n-2+...+B02 0+B-12 -1+B-22 -2+...+B-m2 -m 整数部分 ※ 小数部分 整数部分除以2: (Bn-12 n-1+Bn-22 n-2+... +B1 2 1 +B02 0 ) /2 =(Bn-12 n-2+Bn-22 n-3+...+B12 0 ) ...... B0 第一次商 余数 第一次商/ 2 =(Bn-12 n-3+Bn-22 n-4+...+B22 0 ) ...... B1 第二次商 余数 小数部分乘以2: (B-12 -1+B-22 -2+...+B-m2 -m ) 2 = B-1+ ( B-22 -1+...+B-m2 -m+1 ) 整数 第一次小数 第一次小数×2 = B-2+ ( B-32 -1+...+B-m2 -m+2 ) 整数 第二次小数

例1:(11.625)10=(Bm-1Bm-2B1B0B1B2…)2 整数部分: 整数部分除基数取余数、从低位到高位求各位 数码直到商为0 商 余数 各位数码 11/2=5.....1 Bo 5/2=2.....1 B1 2/2=1.....0 B2 1/2=0......1 B3 (11)10=(1011)2
例1:(11.625)10=(Bn-1Bn-2….B1B0.B-1B-2….. )2 整数部分: 整数部分除基数取余数、从低位到高位求各位 数码直到商为0 商 余数 各位数码 11/2=5......1 B0 5/2 =2......1 B1 2/2 =1......0 B2 1/2 =0......1 B3 (11)10=(1011)2

小数部分: 小数部分乘基数取整数、从高位到低位求各位数码 直到小数部分为0或满足精度要求。 取整数 各位数码 0.625X2=1.25 1 B-1 0.25×2=0.5 0 B-2 0.5×2=1 1 B-3 (0.625)10=(0.101)2 所以:(11.625)10-(1011.101)2
小数部分: 小数部分乘基数取整数、从高位到低位求各位数码 直到小数部分为0或满足精度要求。 取整数 各位数码 0.625×2 = 1.25 1 B-1 0.25×2 = 0.5 0 B-2 0.5×2 =1 1 B-3 (0.625)10=(0.101)2 所以:(11.625)10=(1011.101)2
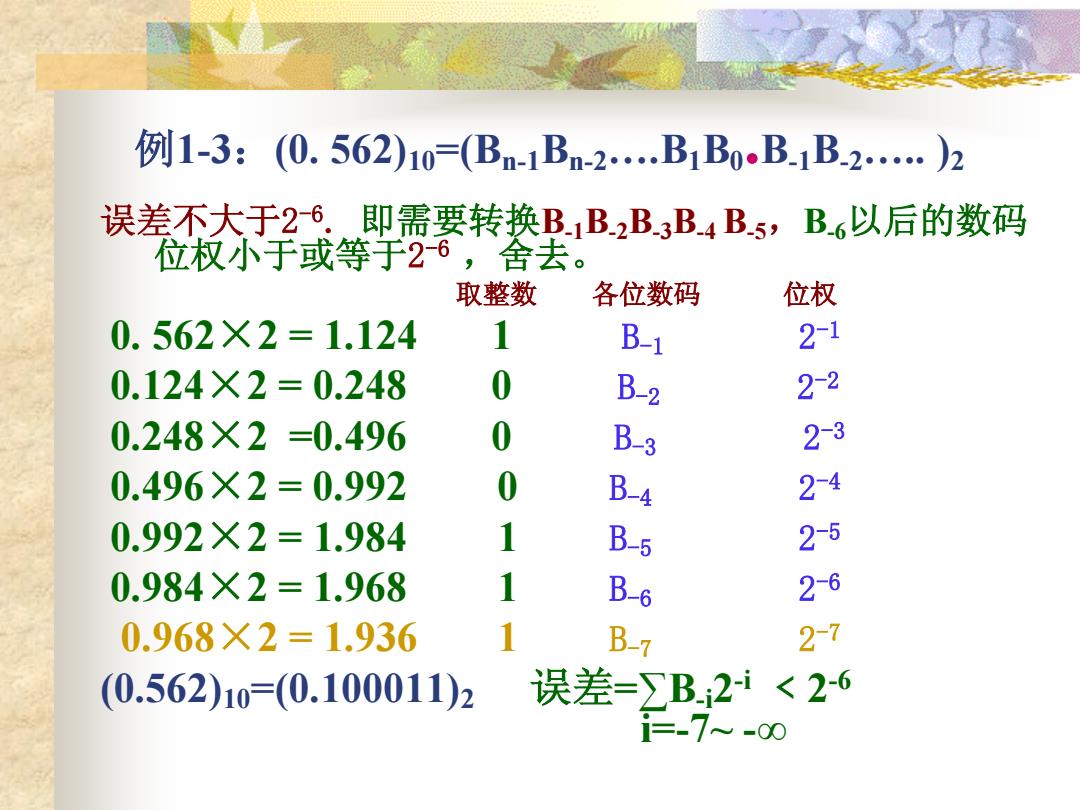
例1-3:(0.562)10=(Bm-1Bn-2B1B0B1B2…)2 误差不大于26,即需要转换B.1B2B3B4B5,B6以后的数码 位权小于或等于26,舍去。 取整数 各位数码 位权 0.562×2=1.124 1 B-1 21 0.124×2=0.248 0 B-2 22 0.248×2=0.496 0 B-3 2-3 0.496×2=0.992 0 B-4 24 0.992X2=1.984 1 B-5 2-5 0.984×2=1.968 1 B-6 2-6 0.968×2=1.936 1 B-7 27 (0.562)10=(0.100011)2 误差=∑B.2i<2-6 iE.7~-00
例1-3:(0. 562)10=(Bn-1Bn-2….B1B0.B-1B-2….. )2 误差不大于2 -6. 即需要转换B-1B-2B-3B-4 B-5,B-6以后的数码 位权小于或等于2 -6 ,舍去。 取整数 各位数码 位权 0. 562×2 = 1.124 1 B-1 2 -1 0.124×2 = 0.248 0 B-2 2 -2 0.248×2 =0.496 0 B-3 2 -3 0.496×2 = 0.992 0 B-4 2 -4 0.992×2 = 1.984 1 B-5 2 -5 0.984×2 = 1.968 1 B-6 2 -6 0.968×2 = 1.936 1 B-7 2 -7 (0.562)10=(0.100011)2 误差=∑B-i2 -i ﹤2 -6 i=-7~ -∞

1.2.3码制 用0和1组合表示信息的编码形式 编码位数和信息量N的关系: N≤2n 一、无符号数的自然二进制代码 n位码表示的数值范围:0~2n-1 编码形式与二进制数完全相同,每位数码有位权的 数值意义(有权码),但每组代码的位数确定 例:8位自然二进制码(表示的数值范围为0~255) 码:00000000,00000101,01111111,10000000,11111111, 数值:0 5 127 128, 255
1.2.3码制 用0和1组合表示信息的编码形式 编码位数n和信息量N的关系: N≤2n 一、无符号数的自然二进制代码 n位码表示的数值范围:0~2n-1 编码形式与二进制数完全相同,每位数码有位权的 数值意义(有权码),但每组代码的位数确定 。 例:8位自然二进制码(表示的数值范围为0~255) 码:00000000,00000101,01111111,10000000,11111111, 数值: 0 , 5 , 127 , 128 , 255