
30 数字图像处理(第三版) 2.4图像取样和量化 由前一节的时论.我们看到有多种获取图像的方法,但在所有这些方法中我们的目的是相同的 就是从感知的数据生成数字图像。多数传感器的输出是连续的电压波 形,这些波形的幅度和空间特性都与感知的物理现象有关。为了产生 一輛数字图像,我们需要把连续的感知数据转换为数字形式。这种转 换包括两种处理:取样和童化 2.4.1取样和量化的基本概念 图2.16说明了取样和量化的基本概念。图2.16(a显示了一幅连续图像人,我们想把它转换为数字 形式。一幅图像的x和y坐标及幅度可能都是连续的。为将它转换为数字形式,必须在坐标上和幅度 上都进行取样操作。对坐标值进行数字化称为取样,对幅值数字化称为量化。 取样 图2.16生成一幅数字图像:(@)连续图像:()连续图像中从A到B的一条主 描线,用于说明取样和量化的概念:(c)取样和量化:()数字扫描线 图2.16(b)中的一维函数是图2.16(a)中沿线段AB的连续图像幅度值(灰度级)的曲线。随机变化 是由图像噪声引起的。为了对该函数取样,我们沿线段AB等间隔地对该函数取样,如图2.16(©)所示 每个样本的空间位置由图形底部的垂直刻废指出。样本用放在函数曲线上的白色小方块表示。这村 的一组离散位置就给出了取样函数。然而,样本值仍(垂直)跨越了灰度值的连续范围。为了形成数 字函数,灰度值也必须转换(量化)为离散量。图2.16()的右侧显示了已分为8个离散区间的灰度制 尺,范围从黑到白。垂直刻度标记指出了赋予8个灰度的每一个特定值。通过对每一样本赋予8个 离散灰度级中的一个来量化连续灰度级。赋值取决于该样本与一个垂直刻度标记的垂直接近程度 取样和量化操作生成的数字样本如图2.16()所示。从该图像的顶部开始逐行执行这一过程,则会 生一幅二维数字图像。图216意味着除了所用的离散级数外,量化所达到的精度强烈地依赖于取样 信号的噪声。 图原 按刚刚讨论的方式取样,假设我们有一辐在两个坐标方向上和幅度上都连续的图像。实践中

第2章数字图像基础 31 动相结合生成时.传成器的命出可用前而寸论的方式量化。然而,空间取样是通过选择客个机械增量 的数量并在取样处激活传感器来收集数据完成的。机械运动可以非常精确地实现,因此从原理上讲。 使用这种方法对一幅图像取样可以到达的精细程度并没有限制。实践中,取样精度的限制由其他因素 决定、譬如系统的光学元件的质量。 当我们使用带状传感器来获取图像时,带中传感器的数量决定了图像中一个方向上的限制。另 个方向上的机械运动可控制得更精确一些,但试图在一个方向上实现超过另一个方向上被传感器数 量限制的取样密度是没有意义的。对传感器输出的量化就完成了产生数字图像的过程。 当传感阵列用于图像获取时,没有运动目 阵列中传感器的数量决定了两个方向上的取样 限制。传感器输出的量化与前述相同。图2.17说 明了这个概念。图2.17(a)显示了投影到一个阵 列传感器平面上的连续图像。图2.17(6)显示了 取样和量化后的图像。很明显 ,数字图像的质 量在很大程度上取决于取样和量化中所用的样 本数和灰度级。姚面正如243节中表明的那 样,在选择这些参数时,图像内容是一个重要 图217(已投影到一个传越器阵列上的连 的考虑因素。 图像:(b)图像取样和量化后的结果 2.4.2数字图像表示 令∫(5,)表示一幅具有两个连续变量s和1的连续图像函数。如前一节解释的那样,通过取样和 量化.我们可把该函数转换为致字图像。假如我们把该连续图像取样为一个二维阵列fx),该阵 列包含有M行和N列,其中(x,y)是离散坐标。为表达清楚和方便起见,我们对这些离散坐标使用 整数值:x=0.1.2.·.M-1和"=0.L.2.·,N-1。这样.数字图像在原点的值就是f(0.0),第- 行中下一个坐标处的值是f0,)。这里,符号(0,)表示第一行的第二个样本,它并不意味着是对图 像取样时的物理坐标值。通常,图像在任何坐标(x,y)处的值记为(x,y),其中x和y都是整数。由 幅图像的坐标张成的实平面部分称为室间域,x和y称为室间变量或空间坐标。 如图2.18所示,有三种基本方法表示f化y)。图2.18()是一幅函数图,用两个坐标轴决定空间位 置,第三个坐标是以两个空间变量x和为函数的武灰度)值。虽然我们可以在这个例子中用该图来 推断图像的结构但是,通常复杂的图像细节太多,以至于很难由这样的图去解译。在处理的元素是 以(x,x)三坐标的形式表达的灰度集时,这种表示是很有用的,其中x和y是空间坐标,2是∫在坐 标(x,y)处的值。在2.6.4节中,我们将探讨这种表示 图2.18(b)是更一般的表示。它显示了f(x,y)出现在监视器或照片上的情况。这里,每个点的灰 度与该点处的f值成正比。该图中仅有三个等间隔的灰度值。如果灰度被归一化到区间0,内,那么 图像中每个点的灰度都有0,0.5或1这样的值。监视器或打印机简单地把这三个值分别变换为黑色、 灰色或白色,如图2.18(6)所示。第三种表示是将fx,y)的数值简单地显示为一个阵列(矩阵)。在这 个例子中,∫的大小为600×600个元素,或360000个数字。很清楚,打印整个矩阵是很麻烦的,且 传达的信息也不多。然而,在开发算法时,当图像的一部分被打印并作为数值进行分析时,这种表示 相当有用。图218()以图形方式传大了放唇令 由前面几节的讨论,我1可得出一个结论,即图2.18(b)和图2.18()中的表示是最有用的。图像 品示允许我们快速地观察结果。数值阵列用于处理和算法开发。以公式形式。我们可将一个M×N网 的数值阵列表示为

数字图像处理(第三版) f0,0 f(o.D) f0,N- f(x.y)= fd.1) fd.N-D (2.41 f(M -1.0)f(M-1.D) fM-1-) 该式的两边以等效的方式定量地表达了一幅数字图像。右边是一个实数矩阵,该矩阵中的每个元素称 为图像单元、图像元素或像素。图像和像素这两个术语将在全书中表示数字图像及其元素。 a b c 厂 888800888888 000 55 000 图2.18(a)画为表面图形的图像;(6)显示为可视灰度阵列的图像;(@)显示 为一个二维数值阵列的图像(0,0.5和1分别表示黑色、灰色和白色) 在某些讨论中,使用传统的矩阵表示法来表示数字图像及其像素更为方便: 4.0 do.N-1 A= a.0 … a1 N-1 2.42) aM-LoaM-L.L…aw-LN- 显然,a=fx=i,y=》=fG,》,因此式(2.41)和式(2.42)是相同的矩阵。我们湛至可以将一幅 图像表示一个向量。例如,尺寸为MN×1的例向量由,的第一M个元素作为A的第一列来构成 下一M个元素作为第二列,等等。我们也可以使用A的行代替列来形成这样的一个向量。只要一致, 哪种表示都是有效的。 简要地回顺图2.18,注意到,数字图像的原点位于左上角,其中正x轴向下延伸,正y轴向右延 伸。这种方便的表示基于这样的事实:许多图像显示(譬如电视显示器)扫描都是从左上角开始的,然 后一次向下移动一行。更重要的事实是矩阵的第一个元素按惯例应在阵列的左上角,因此,将 (x,)的原点选择在左上角于数学上是讲得通的。记住,这种表示是您所熟悉的标准的右手笛卡儿 坐标系统。我们仅说明了指向下方和指向右方的坐标轴来代替向右和向上的坐标轴 有时,以更正式的数学术语表达取样和量化可能会很有用。令Z和R分别表示整数集和实数集 取样处理可看成是把罗平面分为一个网格的过程,网格中每个单元的中心的坐标是笛卡儿积Z2中的 -对元素,Z是所有有序元素对(亿,2)的集合,2和2是Z中的整数。因此,如果(x,)是Z2中的 整数,且f是把灰度值(即实数集R中的一个实数赋给每个特定坐标对(x,y)的一个函数,则f(化,y) ①同忆可知。右手坐标系统是这样一种系统:当正x轴方向向右时。在大搏指竖直向上时,正y轴的方向为垂直于x轴的中指方 向。如图218()所示。事实上这是我们的图像坐标系统情形
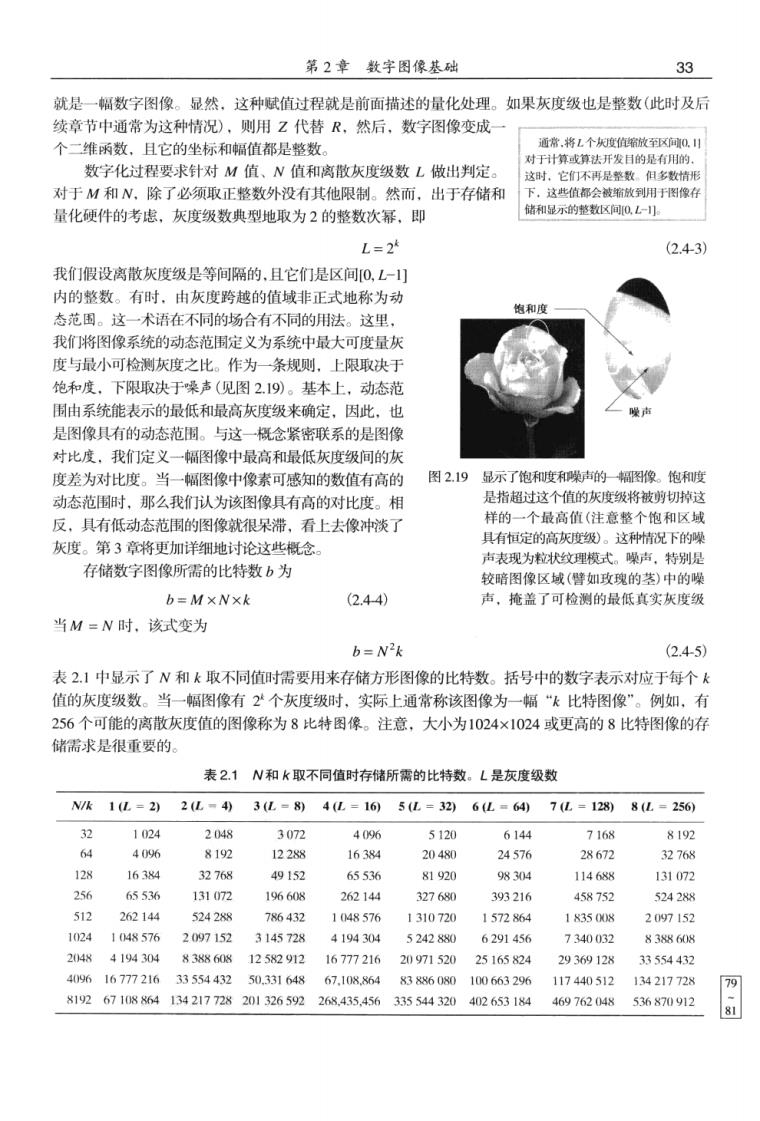
第2章数字图像基础 33 就是幅数字图像。显然,这种赋值过程就是前面描述的量化处理。如果灰度级也是整数(此时及后 续章节中通常为这种情况),则用Z代替R,然后,数字图像变成 个一维项数,目它的华标和幅值都是整数 意.将L个值缩放到区向0. 对于计算或算钛开发日的是有用的 数字化过程要求针对M值、N值和离散灰度级数L做出判定 这时它们不再是整数但多数情州 对于M和N,除了必须取正整数外没有其他限制。然而,出于存储和 图像 量化使件的考虑,灰度级数典型地取为2的整数次幂,即 储和显示的整数区间Q,L小 L=2 (2.43 我们假设离散灰度级是等间隔的.且它们是区间0,L-) 内的整数。有时,由灰度跨越的值域非正式地称为动 和电 态范围。这一术语在不同的场合有不同的用法。这里。 我将图像系统的动态范围定义为系统中最大可度量灰 度与最小可检测灰度之比。作为一条规则上限取决于 饱和度,下限取决于噪声(见图2.19)。基本上,动态范 围由系统能表示的最低和最高灰度级来确定,因此,也 是图像具有的动态范围。与这一一概念紧密联系的是图像 对比度,我们定义一幅图像中最高和最低灰度级间的灰 度差为对比度。当一幅图像中像素可感知的数值有高的 图2.19显示了饱和度和噪声的像。饱和 动态范围时,那么我们认为该图像具有高的对比度。相 是指相过这个值的灰度级将被剪切掉 反,具有低动态范围的图像就很呆滞,看上去像冲淡 样的 个最高值(注意整个饱和区域 灰度。第3章将更加详细地讨论这些概念 具有但定的高灰顶级)。这种竹情况下的 表现为拉状纹理模式。噪声,特别 存储数字图像所需的比特数b为 较暗图像区域(譬如玫瑰的茎)中的噪 b=MxNxk (2.44) 声,掩盖了可检测的最低真实灰度级 当M=N时,该式变为 b=N2k (2.45) 表21中品示了N和人取不同值时需要用来存储方形图像的比特数。括号中的数字表示对应于每个 值的灰度级数。当一幅图像有2个灰度级时,实际上通常称该图像为一幅“k比特图像”。例如,有 256个可能的离散灰度值的图像称为8比特图像。注意.大小为1024×1024或更高的8比特图像的: 储需求是很重要的。 表2.1N和k取不同值时存储所需的比特数。L是灰度级数 Wk1u=22亿-43亿=8)4u=165亿=36u=647亿=128)8u=250 1024 2048 3072 4096 5120 6144 7168 8192 406 8192 122X8 16384 20480 24576 28672 32768 1634 32768 40152 65536 X1U20 0w04 114688 131072 356 66526 131072 19660 262144 327680 303216 458752 5242 512 262144 5242N8 104857 131072 157286 183500 20715 102 1048576 2097152 314572 4194304 5242880 6291430 7340052 83560 24 419430483w860812582912167772162097152025165824 2936912X 33554432 4094167772163355443250.33164867.103,85483886080100663296117440512134217728 8192671084134217728201326592268435,456335544320402653184469762048536s70912 D-