
折半查找算法 int Search_Bin(SSTable ST,KeyType key){ low=1;high=ST.length; 初始化 while (low<=high){ 设置中间值 查找成功,返 mid=(low+high)/2; 回元素位置 if (key==ST.elem[mid].key)return mid; else if (key<ST.elem[mid].key)high=mid-1; else low=mid+1; 在前半部分查找 在后半部分查找 return 0;
int Search_Bin(SSTable ST,KeyType key){ low=1;high=ST.length; while (low<=high){ mid=(low+high)/2; if (key==ST.elem[mid].key) return mid; else if (key<ST.elem[mid].key) high=mid-1; else low=mid+1; } return 0; } 初始化 设置中间值 查找成功,返 回元素位置 在前半部分查找 在后半部分查找 折半查找算法
折半查找的效率 折半查找过程可用一棵二叉树来表示,每个结点表示 表中的一个记录,结点的值对应元素的关键字,结点 上面的数学头冠应的表鱼的位置、树每个根结点 对应当新叁我2间的旯翻2 它的左 子树和右子树分别对应该区间的前半部分和后半部分, 通常把此二叉树称为折半查找的判定树。 判定树:
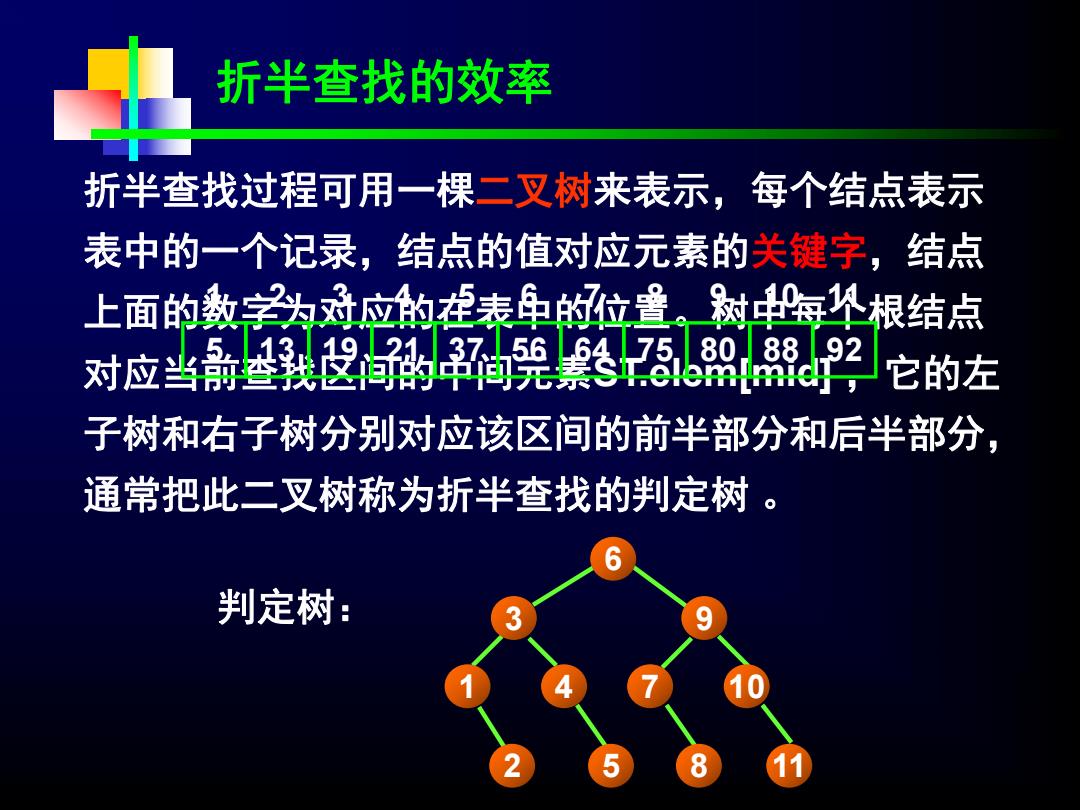
判定树: 折半查找过程可用一棵二叉树来表示,每个结点表示 表中的一个记录,结点的值对应元素的关键字,结点 上面的数字为对应的在表中的位置。树中每个根结点 对应当前查找区间的中间元素ST.elem[mid] ,它的左 子树和右子树分别对应该区间的前半部分和后半部分, 通常把此二叉树称为折半查找的判定树 。 折半查找的效率 2 5 8 11 1 4 7 10 3 9 6 5 1 13 2 19 3 21 4 37 5 56 6 64 7 75 8 80 9 88 10 92 11

折半查找的效率 算法评价 ★判定树:描述查找过程的二叉树叫~ ★有n个结点的判定树的深度为LIog2n+1 ★折半查找法在查找过程中进行的比较次数最多 不超过其判定树的深度 ★折半查找的ASL 设表长n=2-1,h=log2(n+1),即判定树是深度为h的满二叉树 设表中每个记录的查找 概率相等p,= n 则: n n i= n
算法评价 «判定树:描述查找过程的二叉树叫~ «有n个结点的判定树的深度为log2n+1 «折半查找法在查找过程中进行的比较次数最多 不超过其判定树的深度 «折半查找的ASL log ( 1) 1 log ( 1) 1 1 2 1 1 1 2 1, log ( 1), 2 2 1 1 1 1 2 n n n n j n c n ASL p c n p n h n h h j j n i i n i i i i h 则: 设表中每个记录的查找 概率相等 设表长 即判定树是深度为 的满二叉树 折半查找的效率

9.13 索引顺序表的查找 分块查找又称索引顺序表, 它适用于线性表的分 块存储结构(即分块有序表) ★查找过程:将表等分成几块, 块内无序,块间 有序;先确定待查记录所在块,再在块内查找 说明:“分块有序”指的是后一块中的最小关键 字必须大于前一块中最大关键字。 查找分为两步61 89101112131415161718 1确走待奎铯所块顶庐或折线) 2.在块内顺序查找.(只能用顺序查找)
分块查找又称索引顺序表,它适用于线性表的分 块存储结构(即分块有序表)。 « 查找过程:将表等分成几块,块内无序,块间 有序;先确定待查记录所在块,再在块内查找。 说明: “分块有序”指的是后一块中的最小关键 字必须大于前一块中最大关键字。 查找分为两步: 1. 确定待查记录所在块; (顺序或折半查找) 2. 在块内顺序查找. (只能用顺序查找) 9.1.3 索引顺序表的查找 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 22 12 13 8 9 20 33 42 44 38 24 48 60 58 74 57 86 53

索引顺序表的查找 ★适用条件:分块有序表 ★算法实现 冬用数组存放待查记录,每个数据元素至少含有 关键字域 冬建立索引表,每个索引表结点含有最大关键 字域和指向本块第一个结点的指针
« 适用条件:分块有序表 « 算法实现 v用数组存放待查记录,每个数据元素至少含有 关键字域 v建立索引表,每个索引表结点含有最大关键 字域和指向本块第一个结点的指针 索引顺序表的查找