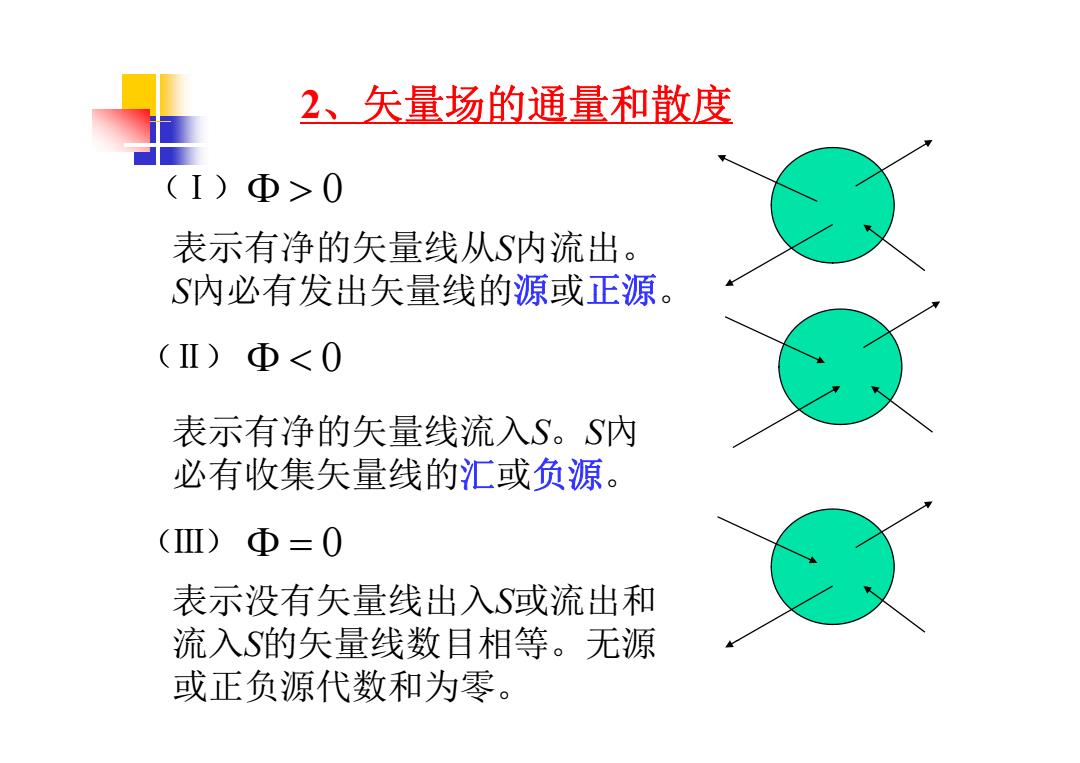
2、矢量场的通量和散度 (I)Φ>0 表示有净的矢量线从S内流出。 S內必有发出矢量线的源或正源。 (Ⅱ)Φ≤0 表示有净的矢量线流入S。S內 必有收集矢量线的汇或负源。 Ⅲ) Φ=0 表示没有矢量线出入S或流出和 流入S的矢量线数目相等。无源 或正负源代数和为零
2、矢量场的通量和散度 (Ⅰ) 0 矢 场的 和散度 表示有净的矢量线从S内流出。 S內必有发出矢量线的源或正源。 (Ⅱ) 0 S內必有发出矢量线的源或正源。 表示有净的矢量线流入S。S內 必有收集矢量线的汇或负源 (Ⅲ) 0 必有收集矢量线的汇或负源。 0 表示没有矢量线出入S或流出和 流入S的矢量线数目相等。无源 或正负源代数和为零

2、矢量场的通量和散度 这种能发出或汇集矢量线的源称为通量源。对 应的场称为具有通量源的场,简称通量场。 ② 散度 矢量场在某点的散度定义为矢量 场在该点单位体积表面的通量。 。因 div Lim JAS △V→0 △V divergence 8x OAx 0A.=V.A △V △S oy 0z
2、矢 场的 和散度 量场的通量和散度 这种能发出或汇集矢量线的源称为通量源。对 ② 散度 这种能发出或汇集矢量线的源称为通量源。对 应的场称为具有通量源的场,简称通量场。 ② 散度 矢量场在某点的散度定义为矢量 场在该点单位体积表面的通量。 A dS ˆ n V A dS divA S V 0 Lim V S A A A A V x y z divergence A x y z
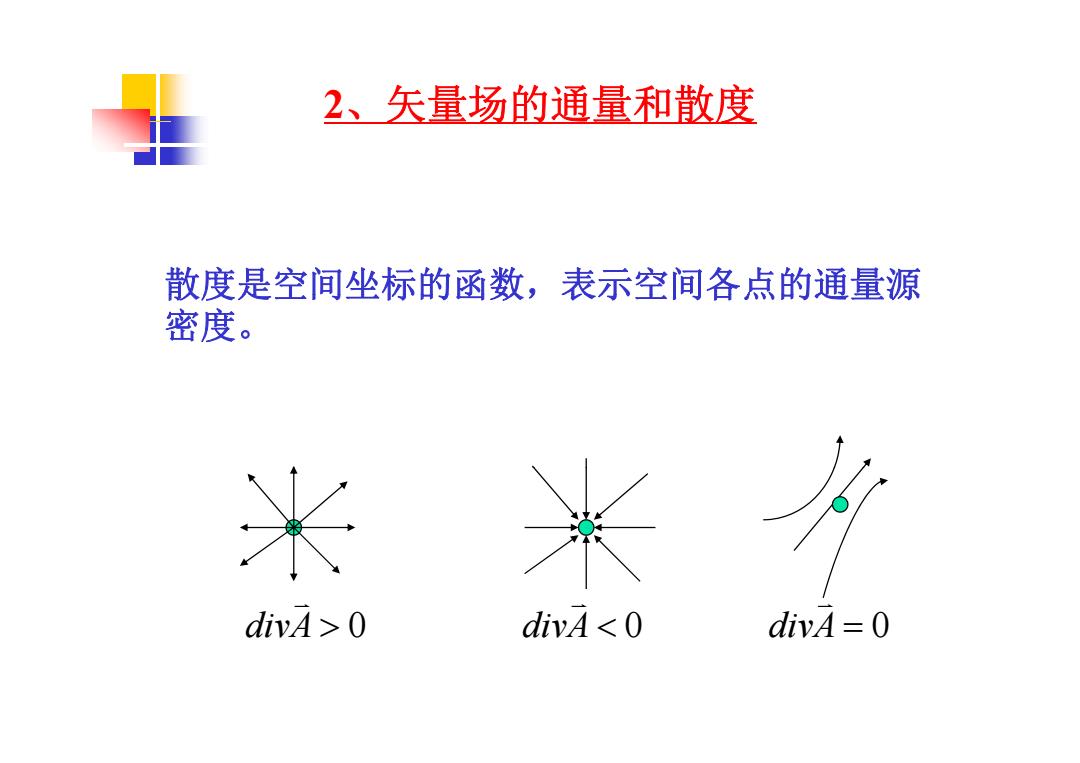
2、矢量场的通量和散度 散度是空间坐标的函数,表示空间各点的通量源 密度。 米米 divA>O divA 0 divA=0
2、矢 场的 和散度 量场的通量和散度 散度是空间坐标的函数,表示空间各点的通量源 密度。 divA 0 divA 0 divA 0

2、矢量场的通量和散度 ③ Gaussi散度定理 [y.ndv=f7.ds 若令为△W0→7.AAV≈f,A·S △V 因此,Gauss定理实际上是将任意点的 散度定义所规定的散度与通量的关系推 广至任意区域
2、矢量场的通量和散度 ③ Gauss散度定理 矢 场的 和散度 AdV A dS V S AdV A dS 若令 为 A A dS 若令V为∆V→0 S A V A dS A dS V A dS A S 因此,Gauss定理实际上是将任意点的 散度定义所规定的散度与通量的关系推 广至任意区域
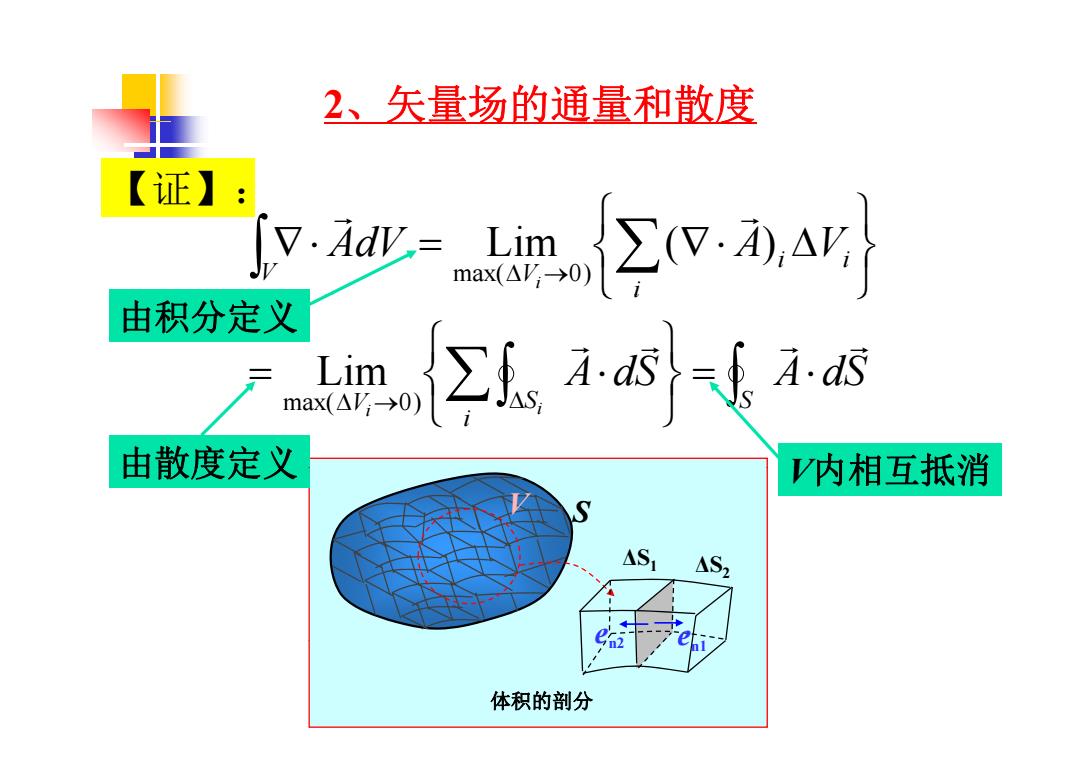
2、矢量场的通量和散度 【证】 w-Σvsr 由积分定义 Lim md 以A.s 由散度定义 V内相互抵消 AS AS2 体积的剖分
2、矢量场的通量和散度 矢 场的 和散度 【证】: i i i V V AdV A V i max( 0) Lim ( ) i A dS A dS Lim 由积分定义 S i V S A dS A dS i i max( 0) Lim 由散度定义 V内相互抵消 V ΔS S 由散度定义 V内相互抵消 ΔS1 ΔS2 e 2 e 1 体积的剖分 n2 en1