
第10卷第5期 智能系统学报 Vol.10 No.5 2015年10月 CAAI Transactions on Intelligent Systems 0ct.2015 D0I:10.11992/is.201410028 网s络出版地址:htp://ww.cmki.net/kcms/detail/23.1538.tp.20150930.1556.016.html 基于密度的统计合并聚类算法 刘贝贝,马儒宁1,丁军娣2 (1.南京航空航天大学理学院,江苏南京211100:2.南京理工大学计算机科学与技术学院,江苏南京210094) 摘要:针对现有聚类算法处理噪声能力差和速度较慢的问题,提出了一种基于密度的统计合并聚类算法(DSMC)。 该算法将数据点的每一个特征看作一组独立随机变量,根据独立有限差分不等式得出统计合并判定准则:同时,结 合数据点的密度信息,把密度从大到小的排序作为凝聚过程中的合并顺序,实现了各类数据点的统计合并。人工数 据集和真实数据集的实验结果表明,DSMC算法不仅可以处理凸状数据集,对于非凸、重叠、加入噪声的数据集也有 良好的聚类效果,充分表明了该算法的适用性和有效性。 关键词:数据点:密度:随机变量:合并:聚类:噪声 中图分类号:0235:TP311文献标志码:A文章编号:1673-4785(2015)05-0712-10 中文引用格式:刘贝贝,马儒宁,丁军娣.基于密度的统计合并聚类算法[J].智能系统学报,2015,10(5):712-721. 英文写引用格式:LIU Beibei,MA Runing,DINGJundi.Density-based statistical merging clustering algorithm[J].CAAI Transac- tions on Intelligent Systems,2015,10(5):712-721. Density-based statistical merging clustering algorithm LIU Beibei',MA Runing',DING Jundi2 (1.College of Science,Nanjing University of Aeronautics and Astronautics,Nanjing 211100,China:2.School of Computer Science and Technology,Nanjing University of Science and Technology,Nanjing 210094,China) Abstract:The ability of existing clustering algorithms to deal with noise is poor,and the speed is slow,instead this paper proposes a density-based statistical merging clustering algorithm (DSMC).The new algorithm takes each group of data points as a set of independent random variables,and gathers statistical criteria from the independent bounded difference inequality.Meanwhile,combined with the density information of the data points,the DSMC al- gorithm takes the descending order of the density as the merging order in the process of condensation,and thereby achieves statistical merging of different types of data points.The experimental results with both artificial datasets and real datasets show that the DSMC algorithm can not only deal with convex data set,and also has good clustering effects on nonconvex shaped,overlapped and noisy,data sets.This proves that the algorithm has good applicability and validity. Keywords:data points;density;random variable;merging;clustering algorithm;noise 聚类2]是数据挖掘领域中十分重要的数据分算法,它的主要特点是在对数据集进行分类之前,需 析技术。具体来说,聚类就是将给定的数据集划分 要事先确定聚类个数,然后将数据集划分到确定好 成互不相交的非空子集的过程。由于初始条件和聚的各类别中。根据划分过程中数据点类别归属的明 类准则的不唯一性,使得各种各样的聚类算法应运确性,又可将分割聚类分为硬聚类和模糊聚类4]。 而生。根据算法形成方式的不同,可以将其分为2 硬聚类中数据点的类别归属是明确的。每个数 大类:基于划分的聚类算法和基于层次的聚类算 据点对各类别的隶属度取0或1,即一个数据点必 法[)。基于划分的聚类算法也可以称为分割聚类 须属于某一类别且只能属于该类别。硬聚类的数学 定义描述如下:设给定的数据集为X={x1,x2,…, 收稿日期:201410-21.网络出版日期:2015-09-30. xn}∈Rx,x,(i=1,2,…,n)表示第i个数据点。预 基金项目:国家自然科学基金资助项目(61103058). 通信作者:丁军娣.E-mail:dingjundi2010@njust..cdu.cn. 先确定将X划分为k个子集C={C,C2,…,C}
第 10 卷第 5 期 智 能 系 统 学 报 Vol.10 №.5 2015 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2015 DOI:10.11992 / tis.201410028 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20150930.1556.016.html 基于密度的统计合并聚类算法 刘贝贝1 ,马儒宁1 ,丁军娣2 (1. 南京航空航天大学 理学院,江苏 南京 211100; 2. 南京理工大学 计算机科学与技术学院,江苏 南京 210094) 摘 要:针对现有聚类算法处理噪声能力差和速度较慢的问题,提出了一种基于密度的统计合并聚类算法(DSMC)。 该算法将数据点的每一个特征看作一组独立随机变量,根据独立有限差分不等式得出统计合并判定准则;同时,结 合数据点的密度信息,把密度从大到小的排序作为凝聚过程中的合并顺序,实现了各类数据点的统计合并。 人工数 据集和真实数据集的实验结果表明,DSMC 算法不仅可以处理凸状数据集,对于非凸、重叠、加入噪声的数据集也有 良好的聚类效果,充分表明了该算法的适用性和有效性。 关键词:数据点;密度;随机变量;合并;聚类;噪声 中图分类号:O235;TP311 文献标志码:A 文章编号:1673⁃4785(2015)05⁃0712⁃10 中文引用格式:刘贝贝,马儒宁,丁军娣. 基于密度的统计合并聚类算法[J]. 智能系统学报, 2015, 10(5): 712⁃721. 英文引用格式:LIU Beibei, MA Runing, DING Jundi. Density⁃based statistical merging clustering algorithm[ J]. CAAI Transac⁃ tions on Intelligent Systems, 2015, 10(5): 712⁃721. Density⁃based statistical merging clustering algorithm LIU Beibei 1 , MA Runing 1 , DING Jundi 2 (1. College of Science, Nanjing University of Aeronautics and Astronautics, Nanjing 211100, China; 2. School of Computer Science and Technology, Nanjing University of Science and Technology, Nanjing 210094, China) Abstract:The ability of existing clustering algorithms to deal with noise is poor, and the speed is slow, instead this paper proposes a density⁃based statistical merging clustering algorithm (DSMC). The new algorithm takes each group of data points as a set of independent random variables, and gathers statistical criteria from the independent bounded difference inequality. Meanwhile, combined with the density information of the data points, the DSMC al⁃ gorithm takes the descending order of the density as the merging order in the process of condensation, and thereby achieves statistical merging of different types of data points. The experimental results with both artificial datasets and real datasets show that the DSMC algorithm can not only deal with convex data set, and also has good clustering effects on nonconvex shaped, overlapped and noisy, data sets. This proves that the algorithm has good applicability and validity. Keywords:data points; density; random variable; merging; clustering algorithm; noise 收稿日期:2014⁃10⁃21. 网络出版日期:2015⁃09⁃30. 基金项目:国家自然科学基金资助项目(61103058). 通信作者:丁军娣. E⁃mail: dingjundi2010@ njust.edu.cn. 聚类[1⁃2]是数据挖掘领域中十分重要的数据分 析技术。 具体来说,聚类就是将给定的数据集划分 成互不相交的非空子集的过程。 由于初始条件和聚 类准则的不唯一性,使得各种各样的聚类算法应运 而生。 根据算法形成方式的不同,可以将其分为 2 大类:基于划分的聚类算法和基于层次的聚类算 法[3] 。 基于划分的聚类算法也可以称为分割聚类 算法,它的主要特点是在对数据集进行分类之前,需 要事先确定聚类个数,然后将数据集划分到确定好 的各类别中。 根据划分过程中数据点类别归属的明 确性,又可将分割聚类分为硬聚类和模糊聚类[ 4 ] 。 硬聚类中数据点的类别归属是明确的。 每个数 据点对各类别的隶属度取 0 或 1,即一个数据点必 须属于某一类别且只能属于该类别。 硬聚类的数学 定义描述如下:设给定的数据集为 X = { x1 ,x2 ,…, xn }∈R n×d ,xi(i = 1,2,…,n)表示第 i 个数据点。 预 先确定将 X 划分为 k 个子集 C = {C1 ,C2 ,…,Ck }

第5期 刘贝贝,等:基于密度的统计合并聚类算法 ·713· (k≤n),则C:满足如下条件:1)C≠⑦,(i=1,2, 凝聚式层次聚类算法[o采用“自底向上”的方 …,k),即每一子集至少含有一个数据点;2)C:∩C= 式进行。一开始将数据集的每个数据点看作一类, ☑,(1≤i≠j≤k),即每个数据点只能属于一个子集: 然后进行一系列的合并操作,直到满足终止条件或 3)UC,=X,即每个数据点必须归属于某一子集。 所有数据点归为一类时停止凝聚。大部分层次聚类 数据点x,(=1,2,…,n)对子集C(i=1,2,…,k)的 算法都是采用凝聚式聚类,代表性的算法有基于代 隶属关系可用隶属函数u:表示,当u:=1时,x:∈ 表点的CURE算法I]、基于稠密点的DBSCAN算 C:,当u=0时,x华C:,其中隶属函数u∈{0,1}且 法I2J、NBC(neighborhood based clustering)算法B] 满足∑4,=1,j,0<∑西,<n,i。硬聚 以及基于核心点的MulCA(multilevel core--sets based aggregation)算法[4]等。 类的代表算法有K-means算法s]和Ncuts(normal- 随着信息技术的迅猛发展,数据源开始不断膨 ized cuts)算法[6]。二者都是致力于得到使目标函 胀,数据结构也变得日渐复杂,具有类内相异、类间 数达到最值的最优聚类。K-means算法取误差平方 相似、噪声和重叠现象的数据集层出不穷,这对于计 和函数作为目标函数,对初始聚类中心和异常点较 算机领域中一些易受噪声点和数据集大小影响的经 为敏感,且面对非凸数据集易陷入局部最优。Ncuts 典聚类算法(如K-means、Ncuts等)来说,是一种巨 算法取规范割函数为目标函数,将数据集的聚类问 大的挑战。 题转化为空间中带权无向图的最优划分问题。 在寻求更优的聚类算法的道路上,人们开始将 Ncuts算法可以聚类任意形状的数据,但大数据聚类 其他专业领域的知识同聚类算法相结合,统计思想 问题对其相似性矩阵的存储和特征向量的计算都是 逐步被应用于聚类算法中。早期统计聚类方法有 种挑战。 GMDD算法[1s]和EM算法[16]等。GMDD算法将数 在模糊聚类中,数据点的类别归属是不明确的, 据点和噪声点看作是由不同混合高斯分布生成的点 一个数据点可以属于所有类别。模糊聚类隶属度的 集,利用一个增强的模型模拟估计含有噪声点的原 取值由硬聚类中只能取0或1变为可以取[0,1]的 始模型。EM算法是一种迭代算法,用于含有隐变 任意值,该值用来表示每个数据点属于各个类别的 量的概率参数模型的最大似然估计或极大后验概率 可能性,仍然满足任意数据点对所有类别的隶属度 估计。2004年,针对复杂的图像分割问题,NoCk和 之和为1。代表性的模糊聚类算法有FCM算法[刀 Nielsen提出了统计区域合并算法(statistical region 和PCM(possibilitic C means)算法[8]。FCM算法利 merging,SRM)u7]。具体地,该算法将像素点作为 用数据点对每一类别的隶属度构成了一个隶属矩 最基本的区域,把像素的3个颜色特征看做3组独 阵,然后将算法的目标函数转变为一个与隶属矩阵 立随机变量,对每一组独立随机变量,根据独立有限 相关的函数,通过优化该目标函数完成聚类。为克 差分不等式得出合并的判定准则,利用像素点梯度 服FCM对噪声敏感的缺点,Krishnapuram和Keller 值从小到大的排序获得合并顺序,依据合并准则和 提出了PCM算法。该算法舍弃了FCM算法中每一 合并顺序,结合像素或区域进行迭代生长。通过控 点对各类别隶属度总和为1的约束条件,使得噪声 制每组独立随机变量的个数,SRM算法实现了对复 点具有很小的隶属度值,从而增加了算法对噪声的 杂图像中目标的快速分割和有效提取。 鲁棒性。 受SRM方法的启发,本文提出了一种基于密度 层次聚类算法又称为树聚类算法。它的主要思 的统计合并聚类算法(density-based statistical mer- 想是对给定的数据集依照相似性矩阵进行层次分 ging clustering,DSMC),该算法主要包括2个步骤: 解,使得聚类结果可以由二叉树或系统树图来描述, 1)根据数据点的密度信息获得合并顺序及每 即树状嵌套结构为H={H,H2,…,H,},(q≤ 数据点的k邻域。首先利用数据点的空间位置信 n),n为数据点的个数,当C:∈Hm,CeH,且m>l, 息及多维特征信息,计算数据点之间的相似性得到 有C:∈C,或C:∩C=对所有i成立,j≠i,m,l= 相似性矩阵,确定每一数据点的k邻域。然后将稠 1,2,…,9。层次聚类算法又分为分裂式和凝聚式 密点与其k邻域中所有点的相似性的最小值作为数 2种。 据点的密度信息,将密度从大到小的排序作为合并 分裂式层次聚类算法采用“自顶向下”的方式 的顺序。 进行。将数据集看作一类,根据类内最大相似性的 2)按照合并顺序依次将稠密点与其k邻域中 原则将数据集逐渐细分,直到满足终止条件或每一 的数据点进行合并判定。将数据点的每个特征看作 个数据点构成一类时停止分裂,例如MONA(mono- 一组独立随机变量,根据独立有限差分不等式得出 thetic analysis)算法[9]和DIANA(divisive analysis) 的合并判定准则判断两点是否合并。当2个数据点 算法[9]等。 对其任意的特征具有相同的期望时,划分为同一类
(k≤n),则 Ci 满足如下条件:1) Ci ≠∅,( i = 1,2, …,k),即每一子集至少含有一个数据点;2)Ci∩Cj = ∅,(1≤i≠j≤k),即每个数据点只能属于一个子集; 3)∪k i=1Ci =X,即每个数据点必须归属于某一子集。 数据点 xj(j = 1,2,…,n)对子集 Ci(i = 1,2,…,k)的 隶属关系可用隶属函数 uij表示,当 uij = 1 时,xj∈ Ci,当 uij = 0 时,xj∉Ci,其中隶属函数 uij∈{0,1}且 满足 ∑ k i = 1 uij = 1,∀j,0 < ∑ n j = 1 uij < n,∀i。 硬聚 类的代表算法有 K⁃means 算法[ 5 ] 和 Ncuts( normal⁃ ized cuts)算法[ 6 ] 。 二者都是致力于得到使目标函 数达到最值的最优聚类。 K⁃means 算法取误差平方 和函数作为目标函数,对初始聚类中心和异常点较 为敏感,且面对非凸数据集易陷入局部最优。 Ncuts 算法取规范割函数为目标函数,将数据集的聚类问 题转化 为 空 间 中 带 权 无 向 图 的 最 优 划 分 问 题。 Ncuts 算法可以聚类任意形状的数据,但大数据聚类 问题对其相似性矩阵的存储和特征向量的计算都是 种挑战。 在模糊聚类中,数据点的类别归属是不明确的, 一个数据点可以属于所有类别。 模糊聚类隶属度的 取值由硬聚类中只能取 0 或 1 变为可以取[0,1]的 任意值,该值用来表示每个数据点属于各个类别的 可能性,仍然满足任意数据点对所有类别的隶属度 之和为 1。 代表性的模糊聚类算法有 FCM 算法[ 7 ] 和 PCM(possibilitic C means)算法[ 8 ] 。 FCM 算法利 用数据点对每一类别的隶属度构成了一个隶属矩 阵,然后将算法的目标函数转变为一个与隶属矩阵 相关的函数,通过优化该目标函数完成聚类。 为克 服 FCM 对噪声敏感的缺点,Krishnapuram 和 Keller 提出了 PCM 算法。 该算法舍弃了 FCM 算法中每一 点对各类别隶属度总和为 1 的约束条件,使得噪声 点具有很小的隶属度值,从而增加了算法对噪声的 鲁棒性。 层次聚类算法又称为树聚类算法。 它的主要思 想是对给定的数据集依照相似性矩阵进行层次分 解,使得聚类结果可以由二叉树或系统树图来描述, 即树状嵌套结构为 H = {H1 , H2 ,…, Hq },( q≤ n),n 为数据点的个数,当 Ci∈Hm , Cj∈Hl且 m>l, 有 Ci∈Cj或 Ci∩Cj = ∅对所有 i 成立,j≠i,m,l = 1,2,…,q。 层次聚类算法又分为分裂式和凝聚式 2 种。 分裂式层次聚类算法采用“自顶向下” 的方式 进行。 将数据集看作一类,根据类内最大相似性的 原则将数据集逐渐细分,直到满足终止条件或每一 个数据点构成一类时停止分裂,例如 MONA(mono⁃ thetic analysis) 算法[9 ] 和 DIANA( divisive analysis) 算法[ 9 ]等。 凝聚式层次聚类算法[10] 采用“自底向上”的方 式进行。 一开始将数据集的每个数据点看作一类, 然后进行一系列的合并操作,直到满足终止条件或 所有数据点归为一类时停止凝聚。 大部分层次聚类 算法都是采用凝聚式聚类,代表性的算法有基于代 表点的 CURE 算法[11 ] 、基于稠密点的 DBSCAN 算 法[1 2 ] 、NBC(neighborhood based clustering)算法[13 ] 、 以及基于核心点的 MulCA(multilevel core⁃sets based aggregation)算法[14 ]等。 随着信息技术的迅猛发展,数据源开始不断膨 胀,数据结构也变得日渐复杂,具有类内相异、类间 相似、噪声和重叠现象的数据集层出不穷,这对于计 算机领域中一些易受噪声点和数据集大小影响的经 典聚类算法(如 K⁃means、Ncuts 等)来说,是一种巨 大的挑战。 在寻求更优的聚类算法的道路上,人们开始将 其他专业领域的知识同聚类算法相结合,统计思想 逐步被应用于聚类算法中。 早期统计聚类方法有 GMDD 算法[1 5 ]和 EM 算法[1 6 ]等。 GMDD 算法将数 据点和噪声点看作是由不同混合高斯分布生成的点 集,利用一个增强的模型模拟估计含有噪声点的原 始模型。 EM 算法是一种迭代算法,用于含有隐变 量的概率参数模型的最大似然估计或极大后验概率 估计。 2004 年,针对复杂的图像分割问题,Nock 和 Nielsen 提出了统计区域合并算法( statistical region merging,SRM) [1 7 ] 。 具体地,该算法将像素点作为 最基本的区域,把像素的 3 个颜色特征看做 3 组独 立随机变量,对每一组独立随机变量,根据独立有限 差分不等式得出合并的判定准则,利用像素点梯度 值从小到大的排序获得合并顺序,依据合并准则和 合并顺序,结合像素或区域进行迭代生长。 通过控 制每组独立随机变量的个数,SRM 算法实现了对复 杂图像中目标的快速分割和有效提取。 受 SRM 方法的启发,本文提出了一种基于密度 的统计合并聚类算法( density⁃based statistical mer⁃ ging clustering,DSMC),该算法主要包括 2 个步骤: 1)根据数据点的密度信息获得合并顺序及每 一数据点的 k 邻域。 首先利用数据点的空间位置信 息及多维特征信息,计算数据点之间的相似性得到 相似性矩阵,确定每一数据点的 k 邻域。 然后将稠 密点与其 k 邻域中所有点的相似性的最小值作为数 据点的密度信息,将密度从大到小的排序作为合并 的顺序。 2) 按照合并顺序依次将稠密点与其 k 邻域中 的数据点进行合并判定。 将数据点的每个特征看作 一组独立随机变量,根据独立有限差分不等式得出 的合并判定准则判断两点是否合并。 当 2 个数据点 对其任意的特征具有相同的期望时,划分为同一类 第 5 期 刘贝贝,等:基于密度的统计合并聚类算法 ·713·

·714 智能系统学报 第10卷 别:当2个数据点对其特征至少有一个期望显著不 该统计模型对数据点及数据点特征的取样是相 同时,划分为不同类别。遍历所有的稠密点,实现对 互独立的。对于Q个独立随机变量的分布没有特 数据集的分类。 定要求,即独立不一定同分布。Q的传统取值一般 相比于上述基于密度的凝聚聚类算法(如DB- 为1,即数据点的每个特征只由一个随机变量表示, SCAN、NBC)DSMC算法在数据点生长合并的过程 但是这一取值对于较小的数据集难以获得可靠的估 中,不仅利用了数据点的密度信息,还利用了根据统 计信息。当Q增大时,数据点的特征可以被描述的 计判定准则得出的数据点每一个特征的差异性信 更加细致,因此,Q成为该算法的重要参数之一。调 息。因此,该算法对噪声具有更好的鲁棒性,也对不 整参数Q,不仅可以改变算法的统计复杂性,还可以 规则形状的数据集和密度不均匀的数据集具有更好 控制分类的精确度。将Q的取值从小调大,可以建 的聚类效果。 立一个层次由粗到细的数据聚类结果。 1 DSM 1.2统计合并判定 DSM算法对数据点的合并由一个特定的统计 1.1统计模型的建立 合并判定准则决定。为了简单起见,先只考虑含有 设给定的数据集为X,包含n个数据点,每个数 一个特征信息的数据集,即一个数据点用一组独立 据点含有多个特征信息,用2={A,B,C,…}表示特 随机变量表示。在此基础上,将得到的结果扩展到 征集合,每个特征的取值范围为[L,U:](i=A,B, 具有更多的特征信息的数据集中。 C,…)。为方便应用,对数据集X作整体移动(特征 为了得出统计合并判定准则,介绍定理如下: 信息整体改变不影响分类),使得特征的取值范围 定理1(独立有限差分不等式[8])设X= 变为[0,g](i=A,B,C,…),其中g:=IU,-Ll。 (X1,X2,…,X)是一组独立随机变量,X的取值范 然后,将数据点的每一个特征用Q个独立随机变量 围为A(k=1,2,…,n)。假设存在一个定义在 表示,每一个随机变量对应一个分布。以特征A为 Π4:的实值函数f,当变量X与X'仅在第k个条件 例,其可表示为A=(A1,A2,…,A),随机变量A (G=1,2,…,Q)对应第j个分布。由于Q个独立 不同时,满足fX)-f(X)1≤r4,则Hr≥0,有 随机变量和的取值应属于[0,g:](i=A,B,C,…), PfX)-u≥)≤exp(-2x2/∑.()) 则每一个随机变量的取值为[0,g,/Q](i=A,B,C, 式中:4为f代X)的期望,即μ=EfX)。 …)。这样,一个数据点的特征信息就由多组独立 根据定理1,可以推出给定数据集X中的不同 随机变量表示。 类别的绝对偏差不等式。记C为数据集X中的类 对于给定的数据集X,假设存在具有完美聚类 别(单个数据点可作为一个类别),1C1为类别内数 结果的数据集X·,那么在X·中,最优的聚类结果 据点的个数,C表示类别C与其他类别合并时的代 具有如下性质:1)同一类别中的数据点,对于任意 表点,E(C)表示该类别相关数据点Q个独立随机 给定的数据特征都具有相同的期望:2)不同的类别 变量期望和的期望。 中的数据点,对于任意给定的数据特征至少有一个 期望不同。这一性质在合并判定过程中起到非常重 推论1考虑数据集X中的类别组合(C1,C2), V0<δ≤1,下面不等式成立的概率不超过6: 要的作用。 I(C-C)-E(G-C)l≥ 数据点x的特征A G*a 11 2 当E(A,=∑E(A).xy 式中:g=max(g:)(i=A,B,C,…)。 =E(A).=∑E(A) 属于同一类别 证明已知类别C,中的数据点可由Q1C,I个 数据点的特征A 当E(4A)f∑E(A)xy 属于同一类别 独立随机变量表示,类别C2中的数据点可由Q1C2 个独立随机变量表示。(C-C)为实值函数,由于 =E(A)=∑E(A) C,C分别是C1,C,的代表点,若变动C中的变量, 「的最大取值为g/(Q1C,I),若变动C2中的变 图12个数据点任一特征聚类的统计说明 量,4的最大取值为g/(Q1C2I)。 Fig.I The statistical description of two data points 记rc,=g/(QC,),6,=g/(Q|C,l),则 clustering about any feature ∑()2=Q(IC,le,)2+IC2lr)2)=
别;当 2 个数据点对其特征至少有一个期望显著不 同时,划分为不同类别。 遍历所有的稠密点,实现对 数据集的分类。 相比于上述基于密度的凝聚聚类算法(如 DB⁃ SCAN、NBC)DSMC 算法在数据点生长合并的过程 中,不仅利用了数据点的密度信息,还利用了根据统 计判定准则得出的数据点每一个特征的差异性信 息。 因此,该算法对噪声具有更好的鲁棒性,也对不 规则形状的数据集和密度不均匀的数据集具有更好 的聚类效果。 1 DSM 1.1 统计模型的建立 设给定的数据集为 X,包含 n 个数据点,每个数 据点含有多个特征信息,用 Ω= {A,B,C,…}表示特 征集合,每个特征的取值范围为[ Li,Ui ] ( i = A,B, C,…)。 为方便应用,对数据集 X 作整体移动(特征 信息整体改变不影响分类),使得特征的取值范围 变为[0, gi ] ( i = A,B,C,…),其中 gi = | Ui -Li | 。 然后,将数据点的每一个特征用 Q 个独立随机变量 表示,每一个随机变量对应一个分布。 以特征 A 为 例,其可表示为 A = (A1 , A2 ,…, AQ ),随机变量 Aj (j = 1, 2,…,Q)对应第 j 个分布。 由于 Q 个独立 随机变量和的取值应属于[0, gi](i = A,B,C,…), 则每一个随机变量的取值为[0, gi / Q] (i = A,B,C, …)。 这样,一个数据点的特征信息就由多组独立 随机变量表示。 对于给定的数据集 X,假设存在具有完美聚类 结果的数据集 X ∗ ,那么在 X ∗ 中,最优的聚类结果 具有如下性质:1) 同一类别中的数据点,对于任意 给定的数据特征都具有相同的期望;2) 不同的类别 中的数据点,对于任意给定的数据特征至少有一个 期望不同。 这一性质在合并判定过程中起到非常重 要的作用。 图 1 2 个数据点任一特征聚类的统计说明 Fig. 1 The statistical description of two data points clustering about any feature 该统计模型对数据点及数据点特征的取样是相 互独立的。 对于 Q 个独立随机变量的分布没有特 定要求,即独立不一定同分布。 Q 的传统取值一般 为 1,即数据点的每个特征只由一个随机变量表示, 但是这一取值对于较小的数据集难以获得可靠的估 计信息。 当 Q 增大时,数据点的特征可以被描述的 更加细致,因此,Q 成为该算法的重要参数之一。 调 整参数 Q,不仅可以改变算法的统计复杂性,还可以 控制分类的精确度。 将 Q 的取值从小调大,可以建 立一个层次由粗到细的数据聚类结果。 1.2 统计合并判定 DSM 算法对数据点的合并由一个特定的统计 合并判定准则决定。 为了简单起见,先只考虑含有 一个特征信息的数据集,即一个数据点用一组独立 随机变量表示。 在此基础上,将得到的结果扩展到 具有更多的特征信息的数据集中。 为了得出统计合并判定准则,介绍定理如下: 定理 1 ( 独立有限差分不等式[1 8 ] ) 设 X = (X1 , X2 ,…, Xn )是一组独立随机变量,Xk的取值范 围为 Ak( k = 1, 2,…, n)。 假设存在一个定义在 ∏kAk 的实值函数 f,当变量 X 与 X′仅在第 k 个条件 不同时,满足| f(X) -f(X′) |≤rk,则∀τ≥0,有 P(f(X) - μ ≥ τ) ≤ exp - 2τ 2 / ∑k rk ( ) 2 ( ) 式中:μ 为 f(X)的期望,即 μ =Ef(X)。 根据定理 1,可以推出给定数据集 X 中的不同 类别的绝对偏差不等式。 记 C 为数据集 X 中的类 别(单个数据点可作为一个类别), | C | 为类别内数 据点的个数,C ( 表示类别 C 与其他类别合并时的代 表点,E(C)表示该类别相关数据点 Q 个独立随机 变量期望和的期望。 推论 1 考虑数据集 X 中的类别组合(C1 ,C2 ), ∀0<δ≤1,下面不等式成立的概率不超过 δ: C1 ( - C2 ( ( ) - E C1 ( - C2 ( ( ) ≥ g 1 2Q 1 C1 + 1 C2 æ è ç ö ø ÷ ln 2 δ 式中:g =max gi ( ) (i = A,B,C,…)。 证明 已知类别 C1 中的数据点可由 Q | C1 | 个 独立随机变量表示,类别 C2 中的数据点可由 Q| C2 | 个独立随机变量表示。 C1 ( -C2 ( ( ) 为实值函数,由于 C1 ( ,C2 ( 分别是 C1 ,C2 的代表点,若变动 C1 中的变量, rk 的最大取值为 g / (Q | C1 | ),若变动 C2 中的变 量,rk 的最大取值为 g / (Q| C2 | )。 记 rC1 = g / (Q C1 ),rC2 = g / (Q C2 ),则 ∑k rk ( ) 2 = Q C1 rC1 ( ) 2 + C2 rC2 ( ) 2 ( ) = ·714· 智 能 系 统 学 报 第 10 卷

第5期 刘贝贝,等:基于密度的统计合并聚类算法 ·715· 由上述合并顺序的获取过程可以看出,k邻域 大小的选择直接影响了数据点密度的大小,进而影 1(11 2 响了DSMC算法的合并顺序。因此,k邻域的大小 根据定理1,取=gG十Gg血谷>0, 也被看作是DSMC算法的一个重要参数。 则 在该算法中,密度的大小不仅受到k邻域的影 P(I(C-C)-E(G-C)l≥ 响,也会受到距离度量(x,y)的影响。针对不同特 征的数据集,选取合适的f(x,y)可以得到更好的聚 171 类结果。在算法中较为常见的距离度量有欧式距 离,马氏距离,最大/最小值距离等。本文实验中主 2r2 < 要应用一种距离度量,它利用数据点最大特征差异 2 进行排序,使得d=max,eks(max(x:-y:),(i=A, 推论得证。 B,C,…),K(x)表示点x的k邻域。随机生成含 由推论1可知,当δ取值接近于零时(本文 有20个点的数据集,选取k邻域大小为4,利用上 若未特别标明,8取为1/(61X12),类别组合 述距离度量,得到DSMC算法的合并顺序如图2 (C,C2)满足不等式1(C-C3)-E(C,-C)1≤ 所示。 b(C1,C2)的概率接近于1,其中b(C1,C2)= 20TG,7G方:若(G,G)可以合并,说 1 明在数据集X·中2者属于同一类别,则有 E(C,-C,)=0。根据这2个前提条件得到如下统计 合并判定准则: ● M(C1,C2)= |ue,1(G-C)l≤b(C,c) false,其他 当类别组合(C,C,)满足|(C-C)|≤ (a)原图 b(C1,C2)时,则合并(C1,C2);反之则不然。 将该准则扩展到具有多个特征信息的数据集 中,形式如下: ftue,a∈{A,B,…f, M(C,C2上 I(G-Ca)|≤b(C,G) false,其他 1.3合并顺序 建立合适的合并准则后,聚类算法的结果受合 并顺序的影响。与随机选取数据点进行合并判定的 算法不同,DSMC算法利用了数据点的密度信息以 获得合并顺序。获取过程可叙述如下:首先,计算数 (b)k=4时的合并顺序 图2DSMC算法的合并顺序 据集中任意2点之间的距离度量(例如欧式距离、 Fig.2 Merging order of DSMC algorithm 最大/最小距离、马氏距离等),获得度量矩阵:然 后,确定每一数据点的k邻域,选取k邻域中所有点 2DSMC算法的实现 与稠密点距离度量的最大值,作为稠密点的局部密 度信息:最后,根据获得的局部密度信息,将所有数 2.1DSMC算法的实现细节 据点按密度从大到小排序,得到算法的合并顺序。 通过对DSMC算法的详细介绍可知,DSMC算 在整个算法过程中,基于密度的合并顺序保证了在 法主要通过2个步骤实现:步骤1是根据数据点的 任意2个不同的类别进行合并判定时,其自身已经 密度信息获得合并顺序及每一数据点的k邻域:步 完成所有可能的合并。 骤2是按照合并顺序依次将稠密点与其k邻域中的
g 2 Q 1 C1 + 1 C2 æ è ç ö ø ÷ 根据定理 1,取 τ = g 1 2Q 1 C1 + 1 C2 æ è ç ö ø ÷ln 2 δ >0, 则 P C1 ( - C2 ( ( ) - E C1 ( - C2 ( ( ( ) ≥ g 1 2Q 1 C1 + 1 C2 æ è ç ö ø ÷ ln 2 δ ö ø ÷ ≤ exp - 2τ 2 ∑k rk ( ) 2 æ è çç ö ø ÷÷ = δ 2 < δ 推论得证。 由推论 1 可知,当 δ 取值接近于零时( 本文 若未 特 别 标 明, δ 取 为 1 / ( 6 | X | 2 ) , 类 别 组 合 ( C1 ,C2 ) 满 足 不 等 式 | C1 ( -C2 ( ( ) - E C1 ( -C2 ( ( ) | ≤ b( C1 ,C2 ) 的 概 率 接 近 于 1, 其 中 b C1 ,C2 ( ) = g 1 2Q ( 1 C1 + 1 C2 )ln 2 δ ;若(C1 ,C2 ) 可以合并,说 明在 数 据 集 X ∗ 中 2 者 属 于 同 一 类 别, 则 有 E(C1 ( -C2 ( )= 0。 根据这 2 个前提条件得到如下统计 合并判定准则: M C1 ,C2 ( ) = true, C1 ( - C1 ( ( ) ≤ b C1 ,C2 ( ) false, 其他 { 当 类 别 组 合 ( C1 , C2 ) 满 足 C1 ( -C2 ( ( ) ≤ b(C1 ,C2 )时,则合并(C1 ,C2 );反之则不然。 将该准则扩展到具有多个特征信息的数据集 中,形式如下: M C1,C2 ( )= true, ∀a ∈{A,B,…}, Ca1 ( - Ca2 ( ( ) ≤b(C1,C2) false,其他 ì î í ï ï ï ï 1.3 合并顺序 建立合适的合并准则后,聚类算法的结果受合 并顺序的影响。 与随机选取数据点进行合并判定的 算法不同,DSMC 算法利用了数据点的密度信息以 获得合并顺序。 获取过程可叙述如下:首先,计算数 据集中任意 2 点之间的距离度量(例如欧式距离、 最大/ 最小距离、马氏距离等),获得度量矩阵;然 后,确定每一数据点的 k 邻域,选取 k 邻域中所有点 与稠密点距离度量的最大值,作为稠密点的局部密 度信息;最后,根据获得的局部密度信息,将所有数 据点按密度从大到小排序,得到算法的合并顺序。 在整个算法过程中,基于密度的合并顺序保证了在 任意 2 个不同的类别进行合并判定时,其自身已经 完成所有可能的合并。 由上述合并顺序的获取过程可以看出,k 邻域 大小的选择直接影响了数据点密度的大小,进而影 响了 DSMC 算法的合并顺序。 因此,k 邻域的大小 也被看作是 DSMC 算法的一个重要参数。 在该算法中,密度的大小不仅受到 k 邻域的影 响,也会受到距离度量 f( x,y)的影响。 针对不同特 征的数据集,选取合适的 f(x,y)可以得到更好的聚 类结果。 在算法中较为常见的距离度量有欧式距 离,马氏距离,最大/ 最小值距离等。 本文实验中主 要应用一种距离度量,它利用数据点最大特征差异 进行排序,使得 d = maxy∈K(x) max xi -yi ( ( ) ) ,( i = A, B, C,…), K( x)表示点 x 的 k 邻域。 随机生成含 有 20 个点的数据集,选取 k 邻域大小为 4,利用上 述距离度量,得到 DSMC 算法的合并顺序如图 2 所示。 (a)原图 (b)k = 4 时的合并顺序 图 2 DSMC 算法的合并顺序 Fig.2 Merging order of DSMC algorithm 2 DSMC 算法的实现 2.1 DSMC 算法的实现细节 通过对 DSMC 算法的详细介绍可知,DSMC 算 法主要通过 2 个步骤实现:步骤 1 是根据数据点的 密度信息获得合并顺序及每一数据点的 k 邻域;步 骤 2 是按照合并顺序依次将稠密点与其 k 邻域中的 第 5 期 刘贝贝,等:基于密度的统计合并聚类算法 ·715·
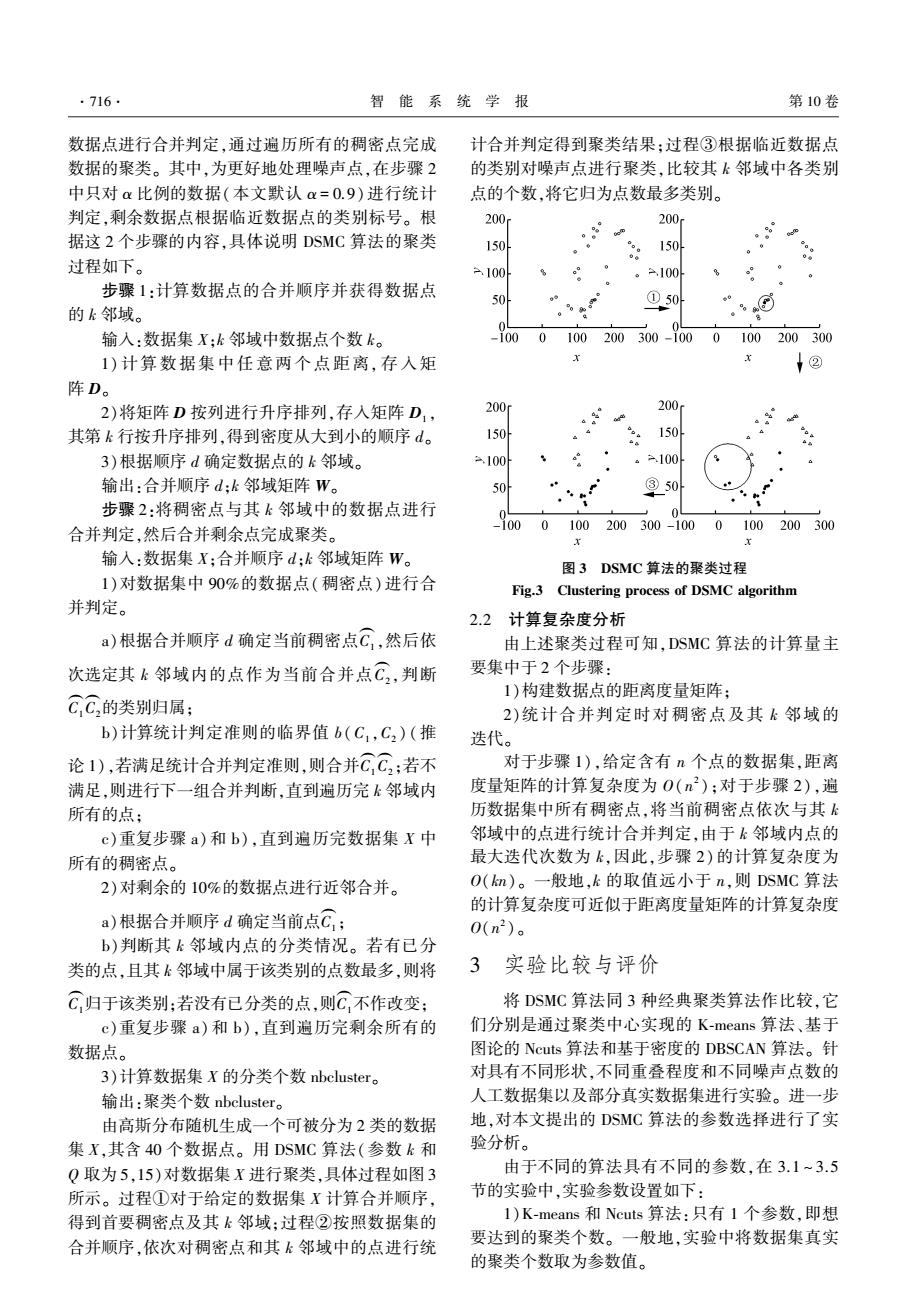
·716 智能系统学报 第10卷 数据点进行合并判定,通过遍历所有的稠密点完成 计合并判定得到聚类结果:过程③根据临近数据点 数据的聚类。其中,为更好地处理噪声点,在步骤2 的类别对噪声点进行聚类,比较其k邻域中各类别 中只对a比例的数据(本文默认α=0.9)进行统计 点的个数,将它归为点数最多类别。 判定,剩余数据点根据临近数据点的类别标号。根 200 200 据这2个步骤的内容,具体说明DSMC算法的聚类 150 150 过程如下。 100 。=.100 步骤1:计算数据点的合并顺序并获得数据点 50 的k邻域。 ①504 %⊙j 输入:数据集X;k邻域中数据点个数k。 1000100 200300-1000100200300 1)计算数据集中任意两个点距离,存入矩 1② 阵D。 2)将矩阵D按列进行升序排列,存入矩阵D, 200 200. 其第k行按升序排列,得到密度从大到小的顺序d。 150 150 3)根据顺序d确定数据点的k邻域。 a.100 。.100 输出:合并顺序d:k邻域矩阵W。 ③50 步骤2:将稠密点与其k邻域中的数据点进行 合并判定,然后合并剩余点完成聚类。 100 0100 200300-1000100200300 x 输入:数据集X;合并顺序d:k邻域矩阵W。 图3DSMC算法的聚类过程 1)对数据集中90%的数据点(稠密点)进行合 Fig.3 Clustering process of DSMC algorithm 并判定。 2.2计算复杂度分析 a)根据合并顺序d确定当前稠密点C,然后依 由上述聚类过程可知,DSMC算法的计算量主 次选定其k邻域内的点作为当前合并点C,判断 要集中于2个步骤: 1)构建数据点的距离度量矩阵: CC的类别归属: 2)统计合并判定时对稠密点及其k邻域的 b)计算统计判定准则的临界值b(C,C2)(推 迭代。 论1),若满足统计合并判定准则,则合并C,C,:若不 对于步骤1),给定含有n个点的数据集,距离 满足,则进行下一组合并判断,直到遍历完k邻域内 度量矩阵的计算复杂度为0(n2):对于步骤2),遍 所有的点: 历数据集中所有稠密点,将当前稠密点依次与其k c)重复步骤a)和b),直到遍历完数据集X中 邻域中的点进行统计合并判定,由于k邻域内点的 所有的稠密点。 最大迭代次数为k,因此,步骤2)的计算复杂度为 2)对剩余的10%的数据点进行近邻合并。 O(km)。一般地,k的取值远小于n,则DSMC算法 的计算复杂度可近似于距离度量矩阵的计算复杂度 a)根据合并顺序d确定当前点C; 0(n2)。 b)判断其k邻域内点的分类情况。若有已分 类的点,且其k邻域中属于该类别的点数最多,则将 3实验比较与评价 C归于该类别:若没有已分类的点,则C,不作改变: 将DSMC算法同3种经典聚类算法作比较,它 c)重复步骤a)和b),直到遍历完剩余所有的 们分别是通过聚类中心实现的K-means算法、基于 数据点。 图论的Ncuts算法和基于密度的DBSCAN算法。针 3)计算数据集X的分类个数nbcluster。 对具有不同形状,不同重叠程度和不同噪声点数的 输出:聚类个数nbcluster. 人工数据集以及部分真实数据集进行实验。进一步 由高斯分布随机生成一个可被分为2类的数据 地,对本文提出的DSMC算法的参数选择进行了实 集X,其含40个数据点。用DSMC算法(参数k和 验分析。 Q取为5,15)对数据集X进行聚类,具体过程如图3 由于不同的算法具有不同的参数,在3.1~3.5 所示。过程①对于给定的数据集X计算合并顺序, 节的实验中,实验参数设置如下: 得到首要稠密点及其k邻域:过程②按照数据集的 1)K-means和Ncuts算法:只有1个参数,即想 合并顺序,依次对稠密点和其k邻域中的点进行统 要达到的聚类个数。一般地,实验中将数据集真实 的聚类个数取为参数值
数据点进行合并判定,通过遍历所有的稠密点完成 数据的聚类。 其中,为更好地处理噪声点,在步骤 2 中只对 α 比例的数据(本文默认 α = 0.9)进行统计 判定,剩余数据点根据临近数据点的类别标号。 根 据这 2 个步骤的内容,具体说明 DSMC 算法的聚类 过程如下。 步骤 1:计算数据点的合并顺序并获得数据点 的 k 邻域。 输入:数据集 X;k 邻域中数据点个数 k。 1) 计 算 数 据 集 中 任 意 两 个 点 距 离, 存 入 矩 阵 D。 2)将矩阵 D 按列进行升序排列,存入矩阵 D1 , 其第 k 行按升序排列,得到密度从大到小的顺序 d。 3)根据顺序 d 确定数据点的 k 邻域。 输出:合并顺序 d;k 邻域矩阵 W。 步骤 2:将稠密点与其 k 邻域中的数据点进行 合并判定,然后合并剩余点完成聚类。 输入:数据集 X;合并顺序 d;k 邻域矩阵 W。 1)对数据集中 90%的数据点(稠密点)进行合 并判定。 a)根据合并顺序 d 确定当前稠密点C1 ( ,然后依 次选定其 k 邻域内的点作为当前合并点C2 ( ,判断 C1 ( C2 ( 的类别归属; b)计算统计判定准则的临界值 b(C1 ,C2 ) (推 论 1),若满足统计合并判定准则,则合并C1 ( C2 ( ;若不 满足,则进行下一组合并判断,直到遍历完 k 邻域内 所有的点; c)重复步骤 a)和 b),直到遍历完数据集 X 中 所有的稠密点。 2)对剩余的 10%的数据点进行近邻合并。 a)根据合并顺序 d 确定当前点C1 ( ; b)判断其 k 邻域内点的分类情况。 若有已分 类的点,且其 k 邻域中属于该类别的点数最多,则将 C1 ( 归于该类别;若没有已分类的点,则C1 ( 不作改变; c)重复步骤 a)和 b),直到遍历完剩余所有的 数据点。 3)计算数据集 X 的分类个数 nbcluster。 输出:聚类个数 nbcluster。 由高斯分布随机生成一个可被分为 2 类的数据 集 X,其含 40 个数据点。 用 DSMC 算法(参数 k 和 Q 取为 5,15)对数据集 X 进行聚类,具体过程如图 3 所示。 过程①对于给定的数据集 X 计算合并顺序, 得到首要稠密点及其 k 邻域;过程②按照数据集的 合并顺序,依次对稠密点和其 k 邻域中的点进行统 计合并判定得到聚类结果;过程③根据临近数据点 的类别对噪声点进行聚类,比较其 k 邻域中各类别 点的个数,将它归为点数最多类别。 图 3 DSMC 算法的聚类过程 Fig.3 Clustering process of DSMC algorithm 2.2 计算复杂度分析 由上述聚类过程可知,DSMC 算法的计算量主 要集中于 2 个步骤: 1)构建数据点的距离度量矩阵; 2)统计合并判定时对稠密点及其 k 邻域的 迭代。 对于步骤 1),给定含有 n 个点的数据集,距离 度量矩阵的计算复杂度为 O(n 2 );对于步骤 2),遍 历数据集中所有稠密点,将当前稠密点依次与其 k 邻域中的点进行统计合并判定,由于 k 邻域内点的 最大迭代次数为 k,因此,步骤 2) 的计算复杂度为 O(kn)。 一般地,k 的取值远小于 n,则 DSMC 算法 的计算复杂度可近似于距离度量矩阵的计算复杂度 O(n 2 )。 3 实验比较与评价 将 DSMC 算法同 3 种经典聚类算法作比较,它 们分别是通过聚类中心实现的 K⁃means 算法、基于 图论的 Ncuts 算法和基于密度的 DBSCAN 算法。 针 对具有不同形状,不同重叠程度和不同噪声点数的 人工数据集以及部分真实数据集进行实验。 进一步 地,对本文提出的 DSMC 算法的参数选择进行了实 验分析。 由于不同的算法具有不同的参数,在 3.1 ~ 3.5 节的实验中,实验参数设置如下: 1)K⁃means 和 Ncuts 算法:只有 1 个参数,即想 要达到的聚类个数。 一般地,实验中将数据集真实 的聚类个数取为参数值。 ·716· 智 能 系 统 学 报 第 10 卷