
4.Bohr理论的成功: •提出了微观体系特有的量子规律:电子轨道角动量量子化 计算出氢原子的轨道半径(r=0.53A,n=1)和基态能级能量E, =-13.6eV,给出量子化的电子轨道和能级能量: r=0.53n2(A) E=-13.6/n2(eV) 能成功应用到类氢离子(如:He*、Li2+、Be3+等) h=0.53n/Z(A)E=-13.6Z21n2(eV) 比较成功地解释了氢原子和类氢离子光谱线 >局限性: ·不能解释氢原子光谱的精细结构和多电子原子的光谱线 经典物理基础+简单量子化条件,自身逻辑上不自洽 ·旧量子论
4. Bohr 理论的成功: •提出了微观体系特有的量子规律:电子轨道角动量量子化 •计算出氢原子的轨道半径(r = 0.53Å, n = 1)和基态能级能量E1 = 13.6 eV,给出量子化的电子轨道和能级能量: •能成功应用到类氢离子(如:He+ 、Li2+、Be3+等) •比较成功地解释了氢原子和类氢离子光谱线 局限性: • 不能解释氢原子光谱的精细结构和多电子原子的光谱线 • 经典物理基础 + 简单量子化条件,自身逻辑上不自洽 • 旧量子论

§7.3原子核外电子的运动状态 >微观粒子运动特点 ·波粒二象性:既有粒子性,又有波动性 ·不确定原理,测不准关系:不能同时测定位置和动量 ·微观粒子与宏观物理的性质和运动规律不同 一、微观粒子的波粒二象性 L.光的波粒二象性(Wave-particle duality) p=mc= mc2 E hv h cccλ ·p动量:粒子性(particle property) ·波长:波动性(wave property) Wave-like and Particle-like Character ·不是经典理论意义上的波或粒子;量子电动力学
微观粒子运动特点 • 波粒二象性:既有粒子性,又有波动性 • 不确定原理,测不准关系:不能同时测定位置和动量 • 微观粒子与宏观物理的性质和运动规律不同 一、微观粒子的波粒二象性 1. 光的波粒二象性 (Wave-particle duality) • p 动量:粒子性(particle property) • λ 波长:波动性(wave property) • Wave-like and Particle-like Character • 不是经典理论意义上的波或粒子;量子电动力学 §7.3 原子核外电子的运动状态 2 mc E h h p mc c cc
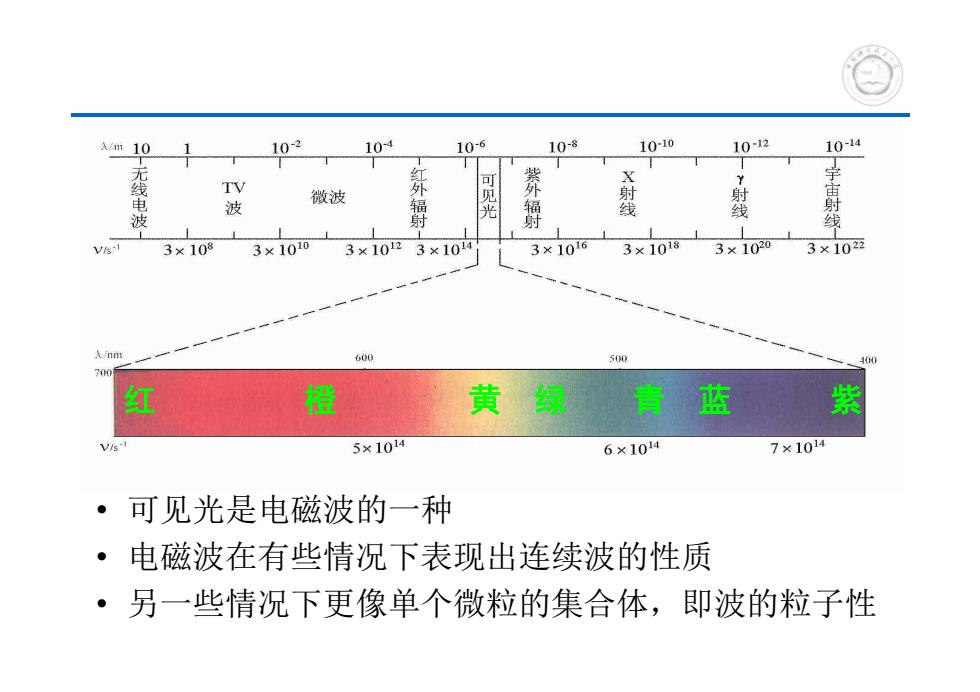
m.101 10-2 104 10-6 10-8 1010 10-12 10-14 线 波 微波 外 见 射 线 线 射 线 Vis-T 3×1083×1010 3×1023×104 3×1016 3×1018 3×1020 3×1022 600 500 700 黄青蓝 5×104 6×1014 7×1014 可见光是电磁波的一种 ·电磁波在有些情况下表现出连续波的性质 ·另一些情况下更像单个微粒的集合体,即波的粒子性
• 可见光是电磁波的一种 • 电磁波在有些情况下表现出连续波的性质 • 另一些情况下更像单个微粒的集合体,即波的粒子性 红 橙 黄绿 青蓝 紫

2.电子的波粒二象性 >de Broglie波:实物微观粒子的运动也具有波粒二象性 p mv 对电子:=h-663×10sx10g1kg)1kgm2 ● -=0.122nm w(9.11×10-2g)5.97>106ms) 1J >电子衍射实验:电场加速电子流通过晶体 .已知能量的电子eV=m2R=?/mv2= h2 mmv2 2meV ·改变电场V,产生不同电子波长=√h/2meV=√150/V(A) ·电子衍射图计算电子射线波长:证实de Broglie波存在 ·宏观物体的de Broglie波?
2. 电子的波粒二象性 de Broglie波:实物微观粒子的运动也具有波粒二象性 • 对电子: 电子衍射实验:电场加速电子流通过晶体 • 已知能量的电子 • 改变电场V,产生不同电子波长 • 电子衍射图计算电子射线波长:证实de Broglie波存在 • 宏观物体的de Broglie波? mv h p h 1 2 2 eV mv 2 2 2 2 22 2 / 2 h h h mv mmv meV 2 h meV V / 2 150 / (Å) 34 3 2 2 28 6 1 6.63 10 (J s) (10 g/1kg) 1kg m s 0.122nm (9.11 10 g)(5.97 10 m s ) 1J h mv 106

二、不确定原理 ·宏观物体运动状态的描述:经典力学 √任一时刻的力学运动状态可确定,轨道运动 √由广义坐标()+广义动量(P)来描述,=6(2P) 。 微观粒子运动状态的描述:量子力学 √波粒二象性: √Heisenberg's不确定原理:微观粒子不可能同时具有确定的 位置和动量 √不是轨道运动,运动状态是量子态 √由波函数平,描述 √满足Schrodinger's方程Hw。=£,a
二、不确定原理 • 宏观物体运动状态的描述:经典力学 任一时刻的力学运动状态可确定,轨道运动 由广义坐标 (zi) + 广义动量 (Pi) 来描述 i = (zi, Pi) • 微观粒子运动状态的描述:量子力学 波粒二象性: Heisenberg’s不确定原理:微观粒子不可能同时具有确定的 位置和动量 不是轨道运动,运动状态是量子态 由波函数a 描述 满足Schrödinger's方程 H a a a ˆ