
西南大学硕士学位论文 2.1.2异形轮的选择 基于上述对圆心轮的优缺点分析,改进后的异形轮有两种较合适的几何模型, 其中一种是保持现有的圆心轮形状,将轮子的轴心(本文所述的轮子轴心指的是 轮子绕该轴心转动,且驱动电机输出轴与该部分出轴或开孔联接)移动至偏离圆 心位置处,如图2-1中(b)部分所示,称之为偏心轮3,14:另一种是保持圆心轮 的轴心不变,将轮子的圆周切割成非完整圆的形状,如图2-1中(c)部分所示, 称之为三叶轮。 图2-1中(b)部分显示偏心轮与圆心轮的区别在于轴心点在偏离圆心点O外 的点O'位置,该轴心点到圆周上各点的距离不同,将OO'的距离称为偏心距e, O'D距离称为最小半径R(min),O'C之间的距离称为最大半径R(max)。可以将这 两个极限径长表示为: R(max)=R+e R(min)=R-e (2-1) 0≤e<R 式中e为正数,取值在0和R之间,当e=0时,即偏心轮的轴心在圆心的位置, 因此可以将圆心轮作为偏心轮的一种特殊状态。从几何形态上可以发现:当固定 偏心轮的轴心点时,绕过轴心转动的部分非轴对称,因此相对于圆心轮有更多搭 在障碍物上的机会和几何突触。当以轮圈绕地面转动时,偏心轮轴心点的离地位 置随着驱动电机的旋转而周期性的高低起伏,并且其高度也是周期性的高低变化, 增加了越过障碍物的可能性。如图中(b)部分轴心点O'在台阶前转动至最高点时 相对于高度为R的障碍物是重心下落的过程,并且径长的不同使得偏心轮容易越 过该障碍物。除此之外,当确定驱动电机的扭矩时,偏心轮圆周上各点的力矩也 就不同,适合用于非结构化的复杂地面。诸如上面所描述的偏心轮作为行走单元 的使用在国内外较为鲜见,西南大学谭兴军、何新强等人曾经以偏心轮作为行走 机构设计出一款偏心轮腿六足机器人],他们的工作重点在于仿生六足昆虫的行 走步态,在取得一定的越障能力的同时失去了高行走效率
西南大学硕士学位论文 2.1.2异形轮的选择 基于上述对圆心轮的优缺点分析,改进后的异形轮有两种较合适的几何模型, 其中一种是保持现有的圆心轮形状,将轮子的轴心(本文所述的轮子轴心指的是 轮子绕该轴心转动,且驱动电机输出轴与该部分出轴或开孔联接)移动至偏离圆 心位置处,如图2.1中(b)部分所示,称之为偏心轮【13’14】;另一种是保持圆心轮 的轴心不变,将轮子的圆周切割成非完整圆的形状,如图2.1中(c)部分所示, 称之为三叶轮。 图2.1中(b)部分显示偏心轮与圆心轮的区别在于轴心点在偏离圆心点O外 的点O’位置,该轴心点到圆周上各点的距离不同,将OO’的距离称为偏心距P, D’D距离称为最小半径R(m蛐,D’C之间的距离称为最大半径R㈣。可以将这 两个极限径长表示为: fR(maX)=R+P {R(min)=R—P (2.1) 【o≤e<尺 式中e为正数,取值在0和R之间,当P=O时,即偏心轮的轴心在圆心的位置, 因此可以将圆心轮作为偏心轮的一种特殊状态。从几何形态上可以发现:当固定 偏心轮的轴心点时,绕过轴心转动的部分非轴对称,因此相对于圆心轮有更多搭 在障碍物上的机会和几何突触。当以轮圈绕地面转动时,偏心轮轴心点的离地位 置随着驱动电机的旋转而周期性的高低起伏,并且其高度也是周期性的高低变化, 增加了越过障碍物的可能性。如图中(b)部分轴心点O’在台阶前转动至最高点时 相对于高度为R的障碍物是重心下落的过程,并且径长的不同使得偏心轮容易越 过该障碍物。除此之外,当确定驱动电机的扭矩时,偏心轮圆周上各点的力矩也 就不同,适合用于非结构化的复杂地面。诸如上面所描述的偏心轮作为行走单元 的使用在国内外较为鲜见,西南大学谭兴军、何新强等人曾经以偏心轮作为行走 机构设计出一款偏心轮腿六足机器人【10】,他们的工作重点在于仿生六足昆虫的行 走步态,在取得一定的越障能力的同时失去了高行走效率。 lO
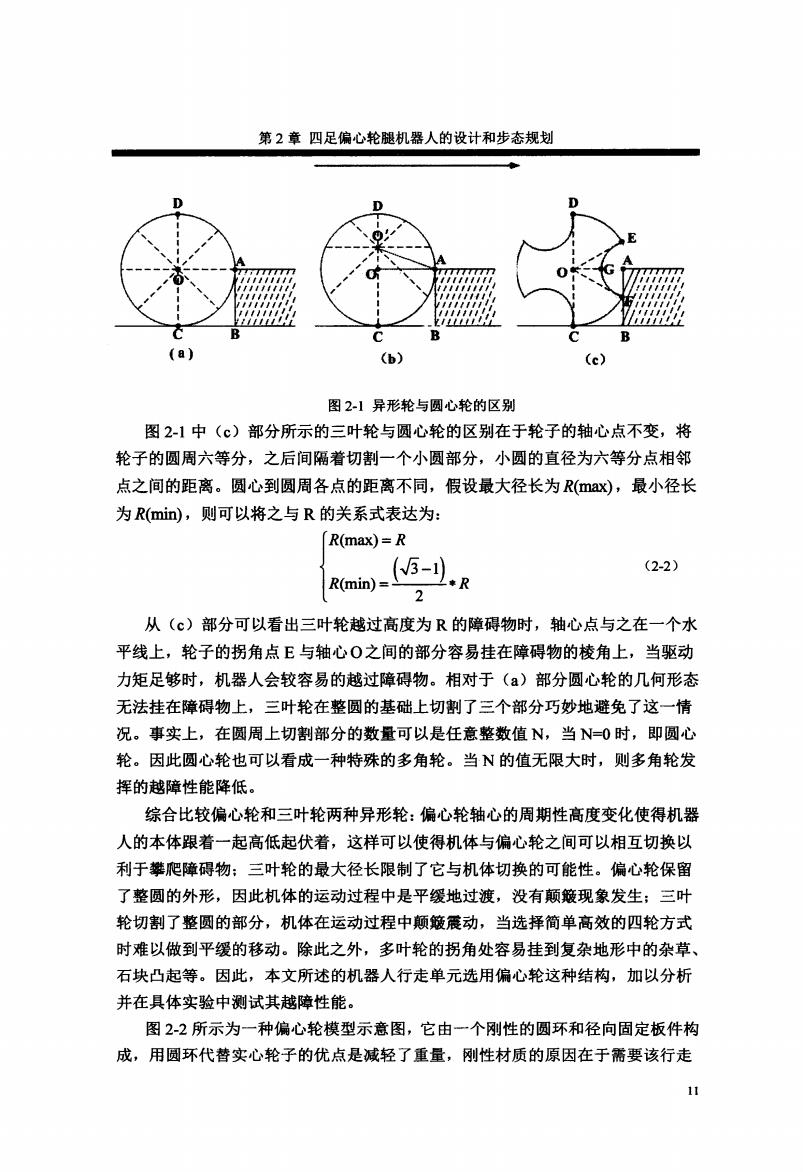
第2章四足偏心轮腿机器人的设计和步态规划 D : a (b) (c) 图2-1异形轮与圆心轮的区别 图2-1中(c)部分所示的三叶轮与圆心轮的区别在于轮子的轴心点不变,将 轮子的圆周六等分,之后间隔着切割一个小圆部分,小圆的直径为六等分点相邻 点之间的距离。圆心到圆周各点的距离不同,假设最大径长为R(ax),最小径长 为R(min),则可以将之与R的关系式表达为: R(max)=R R(min) 5-.R (2-2) 2 从(c)部分可以看出三叶轮越过高度为R的障碍物时,轴心点与之在一个水 平线上,轮子的拐角点E与轴心O之间的部分容易挂在障碍物的棱角上,当驱动 力矩足够时,机器人会较容易的越过障碍物。相对于(a)部分圆心轮的几何形态 无法挂在障碍物上,三叶轮在整圆的基础上切割了三个部分巧妙地避免了这一情 况。事实上,在圆周上切割部分的数量可以是任意整数值N,当N=0时,即圆心 轮。因此圆心轮也可以看成一种特殊的多角轮。当N的值无限大时,则多角轮发 挥的越障性能降低。 综合比较偏心轮和三叶轮两种异形轮:偏心轮轴心的周期性高度变化使得机器 人的本体跟着一起高低起伏着,这样可以使得机体与偏心轮之间可以相互切换以 利于攀爬障碍物:三叶轮的最大径长限制了它与机体切换的可能性。偏心轮保留 了整圆的外形,因此机体的运动过程中是平缓地过渡,没有颠簸现象发生;三叶 轮切割了整圆的部分,机体在运动过程中颠簸震动,当选择简单高效的四轮方式 时难以做到平缓的移动。除此之外,多叶轮的拐角处容易挂到复杂地形中的杂草、 石块凸起等。因此,本文所述的机器人行走单元选用偏心轮这种结构,加以分析 并在具体实验中测试其越障性能。 图2-2所示为一种偏心轮模型示意图,它由一个刚性的圆环和径向固定板件构 成,用圆环代替实心轮子的优点是减轻了重量,刚性材质的原因在于需要该行走 n
第2章四足偏心轮腿机器人的设计和步态规划 D (a) D C B (b) D C B (c) 图2一l异形轮与圆心轮的区别 图2.1中(c)部分所示的三叶轮与圆心轮的区别在于轮子的轴心点不变,将 轮子的圆周六等分,之后间隔着切割一个小圆部分,小圆的直径为六等分点相邻 点之间的距离。圆心到圆周各点的距离不同,假设最大径长为R㈣,最小径长 为R(m蛐,则可以将之与R的关系式表达为: { fR(删2,,、 l√3—1l (2-2) 【R(m证)=L产咄 从(c)部分可以看出三叶轮越过高度为R的障碍物时,轴心点与之在一个水 平线上,轮子的拐角点E与轴心O之间的部分容易挂在障碍物的棱角上,当驱动 力矩足够时,机器人会较容易的越过障碍物。相对于(a)部分圆心轮的几何形态 无法挂在障碍物上,三叶轮在整圆的基础上切割了三个部分巧妙地避免了这一情 况。事实上,在圆周上切割部分的数量可以是任意整数值N,当N=0时,即圆心 轮。因此圆心轮也可以看成一种特殊的多角轮。当N的值无限大时,则多角轮发 挥的越障性能降低。 综合比较偏心轮和三叶轮两种异形轮:偏心轮轴心的周期性高度变化使得机器 人的本体跟着一起高低起伏着,这样可以使得机体与偏心轮之间可以相互切换以 利于攀爬障碍物;三叶轮的最大径长限制了它与机体切换的可能性。偏心轮保留 了整圆的外形,因此机体的运动过程中是平缓地过渡,没有颠簸现象发生;三叶 轮切割了整圆的部分,机体在运动过程中颠簸震动,当选择简单高效的四轮方式 时难以做到平缓的移动。除此之外,多叶轮的拐角处容易挂到复杂地形中的杂草、 石块凸起等。因此,本文所述的机器人行走单元选用偏心轮这种结构,加以分析 并在具体实验中测试其越障性能。 图2.2所示为一种偏心轮模型示意图,它由一个刚性的圆环和径向固定板件构 成,用圆环代替实心轮子的优点是减轻了重量,刚性材质的原因在于需要该行走

西南大学硕士学位论文 单元在高温和尖锐的煤块或石块地形中行走。固定板件一端与圆环内侧固定,另 一端用于和驱动电机输出轴部分固定。固定板的径向长度由偏心距决定,偏心距 越大,该径向长度越小。当偏心距e=0时,该偏心轮和圆心轮等效。 图2-2偏心轮模型 2.2四足偏心轮腿机器人的基本结构 行走单元作为机器人的着地支撑部分和运动部分,确定模型之后,其数量是一 个关键的问题。国内外有关轮式移动机器人的研究,行走单元的数量通常有两轮、 三轮、四轮、六轮、八轮不等,其中最常用的是四轮移动机器人。对于微小型的 机器人,越障要求低,负载需要小,因此两个轮式行走单元便能达到要求,同时 也降低了整个机体的体积。对于一些简单应用的场合,两个主动轮加一个从动轮 的形式也被广泛的应用。对于六个及以上的多轮结构,通常是为了保持机体对地 面的压力稳定,以及分担一点机体的重量。 从控制系统的角度看,系统的部分越少,零部件越简单,则越容易控制:从支 撑机体的稳定性以及分担机体的负载方面,行走单元越多越好:从几何形态上分 析可以得出,三点决定一个平面,因此当机器人本体的重心在机体的中间范围内 时,呈现等腰三角形分布的三个行走单元组成的机器人就可以稳定的支撑着本体 前后移动。但是,对于在非结构化环境中应用的越障机器人来说,三轮结构的机 器人容易在斜面上和凸起障碍物上发生侧翻的现象,并且不能对称的前进和后退。 因此综合考虑需求和实际应用的环境,本文所述的小型机器人采用受独立驱动的 12
西南大学硕士学位论文 单元在高温和尖锐的煤块或石块地形中行走。固定板件一端与圆环内侧固定,另 一端用于和驱动电机输出轴部分固定。固定板的径向长度由偏心距P决定,偏心距 越大,该径向长度越小。当偏心距P=O时,该偏心轮和圆心轮等效。 图2—2偏心轮模型 2.2四足偏心轮腿机器人的基本结构 行走单元作为机器人的着地支撑部分和运动部分,确定模型之后,其数量是一 个关键的问题。国内外有关轮式移动机器人的研究,行走单元的数量通常有两轮、 三轮、四轮、六轮、八轮不等,其中最常用的是四轮移动机器人。对于微小型的 机器人,越障要求低,负载需要小,因此两个轮式行走单元便能达到要求,同时 也降低了整个机体的体积。对于一些简单应用的场合,两个主动轮加一个从动轮 的形式也被广泛的应用。对于六个及以上的多轮结构,通常是为了保持机体对地 面的压力稳定,以及分担一点机体的重量。 从控制系统的角度看,系统的部分越少,零部件越简单,则越容易控制;从支 撑机体的稳定性以及分担机体的负载方面,行走单元越多越好;从几何形态上分 析可以得出,三点决定一个平面,因此当机器人本体的重心在机体的中间范围内 时,呈现等腰三角形分布的三个行走单元组成的机器人就可以稳定的支撑着本体 前后移动。但是,对于在非结构化环境中应用的越障机器人来说,三轮结构的机 器人容易在斜面上和凸起障碍物上发生侧翻的现象,并且不能对称的前进和后退。 因此综合考虑需求和实际应用的环境,本文所述的小型机器人采用受独立驱动的 12

第2章四足偏心轮腿机器人的设计和步态规划 四个偏心轮作为行走单元,基于该偏心轮相对于圆心轮的区别,称之为四足偏心 轮腿机器人。 图23四足偏心轮腿机器人模型 非规则结构环境下的移动机器人可能会发生翻倒现象,为了使机器人翻倒后继 续执行任务,本文所述机器人本体结构采用中心对称设计,理想情况下,将一些 必需的传感器模块封装在机体的盒式箱体内。图2-3所示为四足偏心轮腿机器人的 模型,机身采用扁平长方体盒式箱体结构,箱体内四个拐角位置中心对称地固定 四个型号相同的驱动电机。为了能保证机体的每个行走单元的行走速度和扭矩大 小受到独立的控制,配备四个独立的电机驱动模块以及符合要求的供电模块。电 机通过减速箱减速增加扭矩并延伸输出轴,电机输出轴通过弹性联轴器与偏心轮 的固定板联接,以缓冲机器人在崎岖地形中的颠簸和撞击。箱体以偏心轮轴心点 固定位置为参照前后端延伸相同长度的部分,该延伸段的作用是与偏心轮进行越 障模式的协调工作。 图2-4和2-5所示为四足偏心轮腿机器人的实物样机平台之一,采用的偏心轮 的物理尺寸为:直径=18cm,胎面宽度=1.5cm,偏心距=4.5cm:机器人的主体框架 的物理尺寸为:长×宽×高=50cm×30cm×8cm;样机整体的重量约10Kg。 13
第2章四足偏心轮腿机器人的设计和步态规划 四个偏心轮作为行走单元,基于该偏心轮相对于圆心轮的区别,称之为四足偏心 轮腿机器人。 图2-3四足偏心轮腿机器人模型 非规则结构环境下的移动机器人可能会发生翻倒现象,为了使机器人翻倒后继 续执行任务,本文所述机器人本体结构采用中心对称设计,理想情况下,将一些 必需的传感器模块封装在机体的盒式箱体内。图2.3所示为四足偏心轮腿机器人的 模型,机身采用扁平长方体盒式箱体结构,箱体内四个拐角位置中心对称地固定 四个型号相同的驱动电机。为了能保证机体的每个行走单元的行走速度和扭矩大 小受到独立的控制,配备四个独立的电机驱动模块以及符合要求的供电模块。电 机通过减速箱减速增加扭矩并延伸输出轴,电机输出轴通过弹性联轴器与偏心轮 的固定板联接,以缓冲机器人在崎岖地形中的颠簸和撞击。箱体以偏心轮轴心点 固定位置为参照前后端延伸相同长度的部分,该延伸段的作用是与偏心轮进行越 障模式的协调工作。 图2—4和2—5所示为四足偏心轮腿机器人的实物样机平台之一,采用的偏心轮 的物理尺寸为:直径=18cm,胎面宽度=1.5cm,偏心距=4.5cm;机器人的主体框架 的物理尺寸为:长×宽×高=50cm×30cm×8cm;样机整体的重量约lOKg

西南大学硕士学位论文 图2-4样机正面图 图2-5样机侧面图 2.3四足偏心轮腿机器人的步态规划 偏心轮的主体部分是一个圆形的轮子,只是与电机输出轴固定的轴心部分移 动到了其他位置,因此以偏心轮为行走单元的机器人仍然可以像轮式移动机器人 一样转动行走。然而,偏心轮在转动过程中轴心点的离地高度是周期性的起伏变 化,如果四个独立的偏心轮在转动过程中的转动速度和受驱动时间不同,则最后 四个轴心点并不在一个水平面上。当四个独立的偏心轮固定于一个机器人机身上 时,则四个轴心点被固定在一个水平面,从而在某一个时刻支撑机体的偏心轮数 量可能是2、3或4,因此无法在平整地形中高效率的行走,遇到障碍物时也无法 同时合力越障。所以,对于四足偏心轮腿机器人的特殊行走单元,即便是采用轮 式运动方式也需要按照合理的步态执行。 偏离圆心后的轴心点到轮子圆周上各点的距离不同,当多个偏心轮作为行走 单元固定于同一水平面上的电机出轴时,提供了允许不同分组偏心轮之间的着地 顺序和时间差,因此这些行走单元可以兼做简化版的足和腿式功能,通过模拟动 物的行走步态来控制四足偏心轮腿机器人的腿式行走。例如谭兴军等人的偏心轮 腿六足机器人采用的是经典的三角步态模拟六足昆虫的行走15,I6,17.18剧。 2.3.1轮式运动步态 以电机驱动轮子旋转一周为一个周期来分析,圆心轮的周期性运动状态从轮子 的外观和轴心点(即圆心点)上看不出有明显的变化,而偏心轮的运动状态中轴 心点(偏离圆心的点)的相对位置却呈现出周期性的变化。 4
西南大学硕士学位论文 图2—4样机正面图 图2—5样机侧面图 2.3四足偏心轮腿机器人的步态规划 偏心轮的主体部分是一个圆形的轮子,只是与电机输出轴固定的轴心部分移 动到了其他位置,因此以偏心轮为行走单元的机器人仍然可以像轮式移动机器人 一样转动行走。然而,偏心轮在转动过程中轴心点的离地高度是周期性的起伏变 化,如果四个独立的偏心轮在转动过程中的转动速度和受驱动时间不同,则最后 四个轴心点并不在一个水平面上。当四个独立的偏心轮固定于一个机器人机身上 时,则四个轴心点被固定在一个水平面,从而在某一个时刻支撑机体的偏心轮数 量可能是2、3或4,因此无法在平整地形中高效率的行走,遇到障碍物时也无法 同时合力越障。所以,对于四足偏心轮腿机器人的特殊行走单元,即便是采用轮 式运动方式也需要按照合理的步态执行。 偏离圆心后的轴心点到轮子圆周上各点的距离不同,当多个偏心轮作为行走 单元固定于同一水平面上的电机出轴时,提供了允许不同分组偏心轮之间的着地 顺序和时间差,因此这些行走单元可以兼做简化版的足和腿式功能,通过模拟动 物的行走步态来控制四足偏心轮腿机器人的腿式行走。例如谭兴军等人的偏心轮 腿六足机器人采用的是经典的三角步态模拟六足昆虫的行走[15,16,17,18】。 2.3.1轮式运动步态 以电机驱动轮子旋转一周为一个周期来分析,圆心轮的周期性运动状态从轮子 的外观和轴心点(即圆心点)上看不出有明显的变化,而偏心轮的运动状态中轴 心点(偏离圆心的点)的相对位置却呈现出周期性的变化。 14