上海交通大学：《热力学 Thermodynamics（I）》课程教学资源（课件讲义）Lecture 46_Diesel cycle and dual cycle

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY Engineering Thermodynamics I Lecture 46 Chapter 9 Gas Power Cycles Spring,2017 Prof.,Dr.Yonghua HUANG 强 AR是r 目e http://cc.sjtu.edu.cn/G2S/site/thermo.html 1日G

Engineering Thermodynamics I Lecture 46 Spring, 2017 Prof., Dr. Yonghua HUANG Chapter 9 Gas Power Cycles http://cc.sjtu.edu.cn/G2S/site/thermo.html

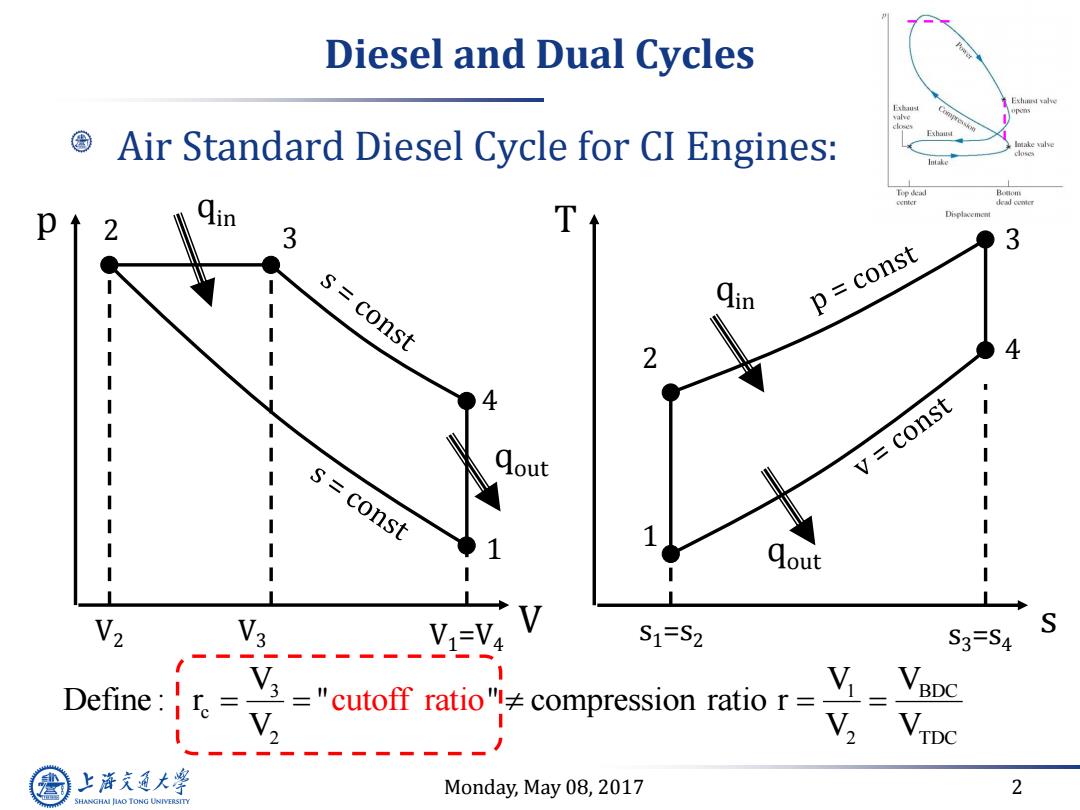
Diesel and Dual Cycles ns Exbaud Air Standard Diesel Cycle for CI Engines: Top dead p 2 3 s=const p const 4 const V s=const I 1 1 1 Qout V3 V1=V4 S1=S2 S3=S4 Define: Y3 ="cutoff ratio"compression ratio r= V, 八---22---2- 上降文通大学 Monday,May 08,2017 2 SHANGHAI JIAO TONG UNIVERSITY

Monday, May 08, 2017 2 Diesel and Dual Cycles Air Standard Diesel Cycle for CI Engines: qout s T 1 2 4 3 s1=s2 s3=s4 qin qout V p 1 2 4 3 V1=V4 qin V2 V3 3 BDC 1 c 2 2 TDC V V V Define : r " " compression ratio r V V cutoff ratio V     

Continue Diesel Cycle s=const Diesel Cycle Energy Balances: const Assuming: V V3 V1=V4 ·w=0 only during heat transfer4→1；△KE=△PE=0 Air is ideal gas,constant specific heats du=0 Wnet W23 W34-W121 qin -lqoutl ·during process2→3，wis≠0(change in volume) qin-W23=(u3-u2) →qin=(u3-u2)+W23=(u3-u2)+P23(V3-V2) =h3-h2 dout U4 -U1 上游通大学 Monday,May 08,2017 3 SHANGHAI JIAO TONG UNIVERSITY

Monday, May 08, 2017 3 Continue Diesel Cycle Diesel Cycle Energy Balances: • Assuming: • w = 0 only during heat transfer 4 1; DKE = DPE = 0 • Air is ideal gas, constant specific heats wnet = w23 + w34 – |w12| = qin – |qout| • during process 2 3, w is ≠0 (change in volume) qin – w23= (u3 – u2 ) qin = (u3 – u2 ) + w23 = (u3 – u2 ) + p23 (v3 – v2 ) = h3 – h2 qout = u4 – u1 d 0 u   V p 1 2 4 3 V1=V4 qin V2 V3

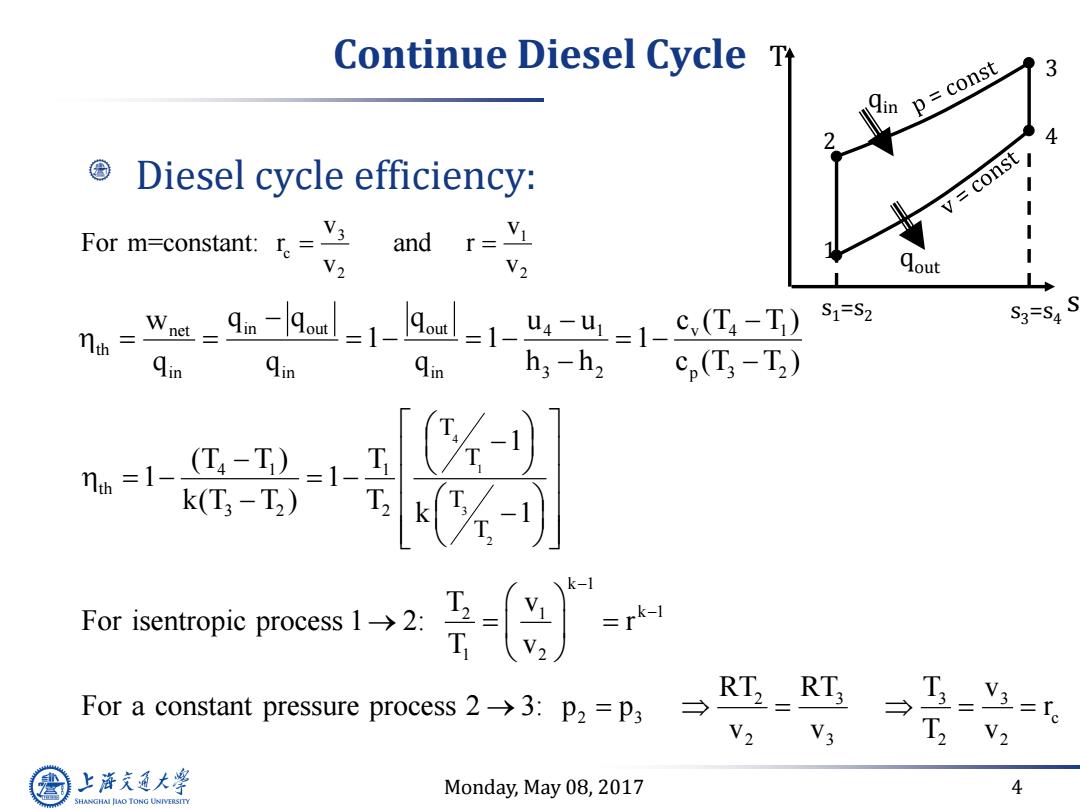
Continue Diesel Cycle T p=const Diesel cycle efficiency: v=const For m-constant:=v and r=V I V2 V2 Qout wu-9。-l9m-1-Aa-1-u-u=1-c,L-T )S1=S2 S3= Qin h3-h2 cp(T;-T2) k(T3-T2) k-1 For isentropie proces: =r For a constant pressure process2→3：p2=p3→ RT2 RT; T V2 V3 上游充通大 Monday,May 08,2017 4 SHANGHAI JIAO TONG UNIVERSITY

Monday, May 08, 2017 4 Continue Diesel Cycle Diesel cycle efficiency: 3 1 c 2 2 v v For m=constant: r and r v v   s T 1 2 4 3 s1=s2 s3=s4 qin qout net v 4 1 in out out 4 1 th in in in 3 2 p 3 2 w c (T T ) q q q u u 1 1 1 q q q h h c (T T )               4 1 3 2 4 1 1 th 3 2 2 T T T T 1 (T T ) T 1 1 k(T T ) T k 1                            k 1 2 1 k 1 1 2 T v For isentropic process 1 2: r T v            2 3 3 3 2 3 c 2 3 2 2 RT RT T v For a constant pressure process 2 3: p p r v v T v       

Continue Diesel Cycle 3 s const Continue Diesel cycle efficiency: const T For isentropic process3→4： T V2 V3 V1=V4 Then,r 1 =1- 1-1 T k。-1) (const.k) ≥1 Thus,for a given r:nt.Diesel <nth.o! 上游通大学 Monday,May 08,2017 5 SHANGHAI JLAO TONG UNIVERSITY

Monday, May 08, 2017 5 Continue Diesel Cycle Continue Diesel cycle efficiency: k 1 k 1 k 1 k 1 2 k 1 2 3 4 1 1 1 2 2 k 1 k 1 4 3 3 3 3 1 3 k 1 k 1 k 4 3 3 3 3 3 k c 1 2 2 2 2 2 For isentropic process 3 4: T V T V V V T T V T V V V V T V T T V V V V r T T V V V V                                                         k 1 2 1 1 2 T v T v         (const. k) 4 1 3 2 k c k 1 th 2 1 c 1 T T T T 1 T Then, 1 T k 1 1 r 1 1 r k(r 1)                              V p 1 2 4 3 V1=V4 qin V2 V3 Thus, for a given r : !    th,Diesel th,Otto