
第1卷第2期 智能系统学报 Vol.1№2 2006年10月 CAAI Transactions on Intelligent Systems 0ct.2006 基于有限状态自动机的服务组合模型 蒋运承12,汤庸2,邓培民 (1.广西师范大学计算机科学与信息工程学院,广西桂林541004:2.中山大学计算机科学系,广东广州510275) 摘要:分析了目前服务计算的研究现状和存在的问题,在D Berardi和A Wombacher的基础上提出了一种带条件 的有限状态自动机模型cFSA(Finite State Automata with condition),并给出了基于cFSA的服务理论模型.在该服 务理论模型的基础上提出了一种基于有限状态自动机的服务组合形式化模型,并给出了该模型的代数性质和实现 方法 关键词:有限状态自动机:带条件的有限状态自动机:服务计算:服务组合 中图分类号:TP18文献标识码:A文章编号:1673-4785(2006)02-004810 A service composition model based on finite state automata JIANG Yumcheng'2,TANG Yong?,DENG Pei-min' (1.College of Computer Sciences and Information Engineering,Guangxi Normal University,Guilin 541004,China;2.De- partment of Computer Sciences,Sun Yasen University,Guangzhou 510275,China) Abstract:The existing conditions and problems of service computing are analyzed,and based on the work of D Berardi and A Wombacher,a kind of finite state automata with condition cFSA(Finite State Automata with condition)is presented,and the service theory model based on cFSA is presented too.Based on this model,the formal theory model of service composition based on finite state automata with condition cFSA is studied.The algebraic property and implementing method of the service composition model are studied. Key words :finite state automata;finite state automata with condition;service computing;service composition 面向服务的计算山(service-oriented compu- Microsoft将WSFL和LANG结合起来提出了服 ting)是一种新的分布式计算范型,它以服务作为开 务组合语言BPEL4WSo1,蒋运承研究了面向服务 发应用或提供问题解决方案的基本元素.而服务是 质量的服务匹配算法山等. 一种自描述的、平台无关的计算元素,它支持分布式 但是,目前e-Service的研究中,主要将服务看 应用的快速和低价组合.例如,目前的Web服务2)、 成是一个无状态的动作,事实上这是不充分的,服务 语义Web服务)或基于主体的服务4等都是面向应该是一个有状态的动作序列1),这方面已有研 服务的计算范型,文中统称为服务或e-Service. 究.例如,D.Berardi用有限状态自动机来建立Web 目前国内外对e-Service进行了深入研究,W3C 服务的理论模型,但D.Berardi的工作只研究了服 提出了Web服务描述语言WSDL I5I,D Martin基 务描述与有限状态自动机的转换问题,没有研究基 于OWL提出了语义Web服务本体OWL-s),史 于有限状态自动机的服务匹配和组合问题】.A 忠植利用描述逻辑理论来描述主体服务),蒋运承 Wombacher研究了基于有限状态自动机的Web服 提出了主体服务描述语言SDL SINI4,并且这些服 务商业过程的匹配问题,但A Wombacher也没有 务描述语言都有相应的服务匹配算法.BM根据工 研究基于有限状态自动机的服务组合问题).本文 作流的思想提出了Web服务流语言WSFLI81,Mi 进一步研究了基于有限状态自动机的服务组合问 crosoft提出了服务组合语言LANG),BM和 题 收稿日期:200602-23. 1 服务理论模型 基金项目:国家自然科学基金资助项目(60373081);广东省自然科 学重点基金资助项目(04105503) 为了用有限状态自动机来描述服务,下面先给 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
第 1 卷第 2 期 智 能 系 统 学 报 Vol. 1 №. 2 2006 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2006 基于有限状态自动机的服务组合模型 蒋运承1 ,2 ,汤 庸2 ,邓培民1 (1. 广西师范大学 计算机科学与信息工程学院 ,广西 桂林 541004 ; 2. 中山大学 计算机科学系 ,广东 广州 510275) 摘 要 :分析了目前服务计算的研究现状和存在的问题 ,在 D Berardi 和 A Wombacher 的基础上提出了一种带条件 的有限状态自动机模型 cFSA ( Finite State Automata with condition) ,并给出了基于 cFSA 的服务理论模型. 在该服 务理论模型的基础上提出了一种基于有限状态自动机的服务组合形式化模型 ,并给出了该模型的代数性质和实现 方法. 关键词 :有限状态自动机 ;带条件的有限状态自动机 ;服务计算 ;服务组合 中图分类号 : TP18 文献标识码 :A 文章编号 :167324785 (2006) 0220048210 A service composition model based on finite state automata J IAN G Yun2cheng 1 ,2 , TAN G Yong 2 , DEN G Pei2min 1 (1. College of Computer Sciences and Information Engineering , Guangxi Normal University , Guilin 541004 , China ; 2. De2 partment of Computer Sciences , Sun Ya2sen University , Guangzhou 510275 , China) Abstract :The existing conditions and problems of service comp uting are analyzed , and based on t he work of D Berardi and A Wombacher , a kind of finite state automata with condition cFSA (Finite State Automata with condition) is presented , and t he service theory model based on cFSA is presented too. Based on this model , t he formal theory model of service compo sition based on finite state automata with condition cFSA is st udied. The algebraic property and implementing met hod of t he service composition model are studied. Keywords :finite state automata ; finite state automata with condition ; service computing ; service composition 收稿日期 :2006202223. 基金项目 :国家自然科学基金资助项目(60373081) ; 广东省自然科 学重点基金资助项目(04105503) . 面向服务的计算[1 ] ( service2oriented comp u2 ting) 是一种新的分布式计算范型 ,它以服务作为开 发应用或提供问题解决方案的基本元素. 而服务是 一种自描述的、平台无关的计算元素 ,它支持分布式 应用的快速和低价组合. 例如 ,目前的 Web 服务[2 ] 、 语义 Web 服务[3 ] 或基于主体的服务[4 ] 等都是面向 服务的计算范型 ,文中统称为服务或 e2Service. 目前国内外对 e2Service 进行了深入研究 ,W3C 提出了 Web 服务描述语言 WSDL [5 ] ,D Martin 基 于 OWL 提出了语义 Web 服务本体 OWL2S [6 ] ,史 忠植利用描述逻辑理论来描述主体服务[7 ] ,蒋运承 提出了主体服务描述语言 SDLSIN [4 ] ,并且这些服 务描述语言都有相应的服务匹配算法. IBM 根据工 作流的思想提出了 Web 服务流语言 WSFL [ 8 ] ,Mi2 cro soft 提出了服务组合语言 XLAN G [9 ] , IBM 和 Microsoft 将 WSFL 和 XLAN G结合起来提出了服 务组合语言 BPEL4WS [10 ] ,蒋运承研究了面向服务 质量的服务匹配算法[11 ]等. 但是 ,目前 e2Service 的研究中 ,主要将服务看 成是一个无状态的动作 ,事实上这是不充分的 ,服务 应该是一个有状态的动作序列[12213 ] ,这方面已有研 究. 例如 ,D. Berardi 用有限状态自动机来建立 Web 服务的理论模型 ,但 D. Berardi 的工作只研究了服 务描述与有限状态自动机的转换问题 ,没有研究基 于有限状态自动机的服务匹配和组合问题[12 ] . A Wombacher 研究了基于有限状态自动机的 Web 服 务商业过程的匹配问题 ,但 A Wombacher 也没有 研究基于有限状态自动机的服务组合问题[13 ] . 本文 进一步研究了基于有限状态自动机的服务组合问 题. 1 服务理论模型 为了用有限状态自动机来描述服务 ,下面先给
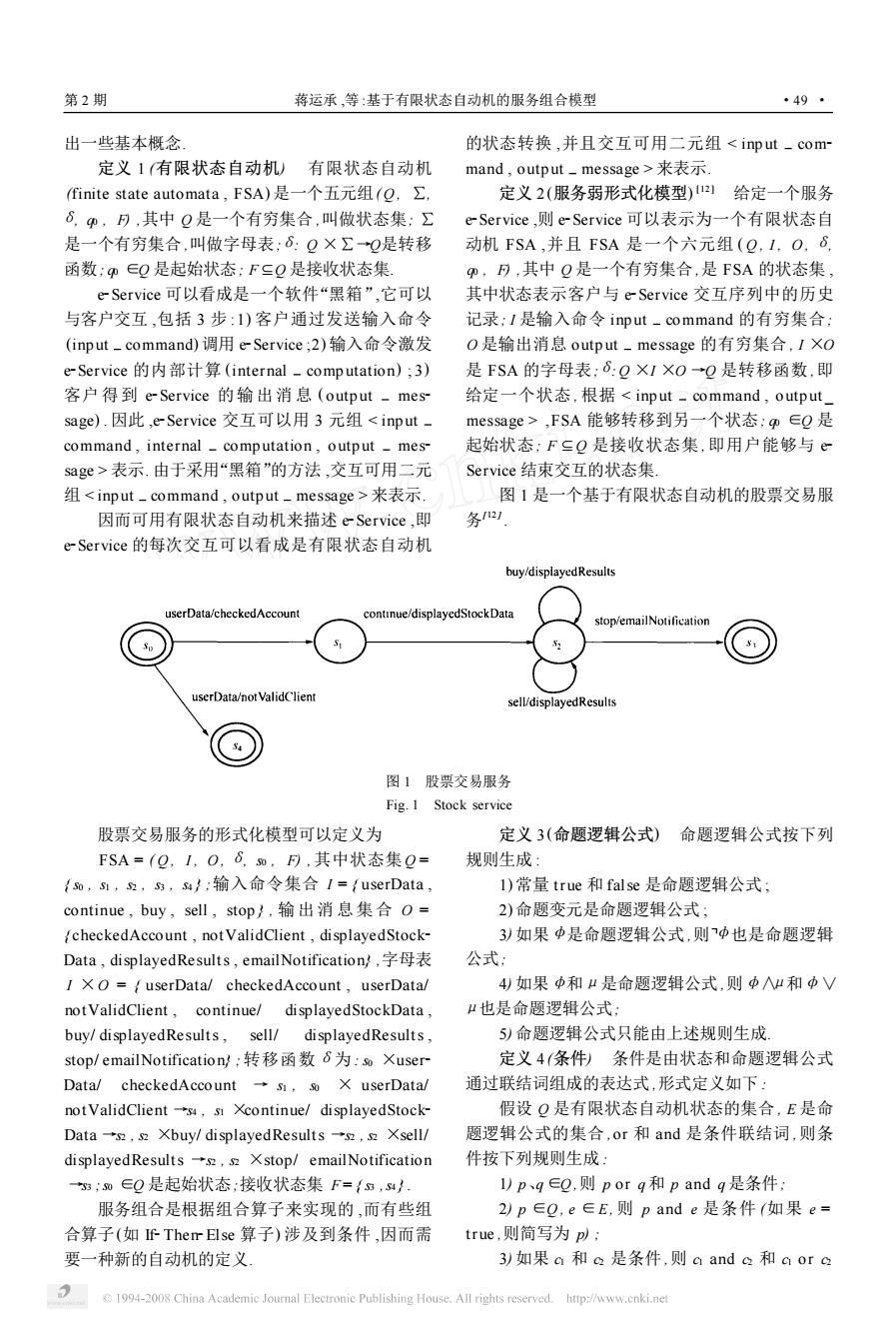
第2期 蒋运承,等:基于有限状态自动机的服务组合模型 ·49· 出一些基本概念 的状态转换,并且交互可用二元组<iput-com- 定义1(有限状态自动机)有限状态自动机 mand,output-message>来表示 finite state automata,FSA)是一个五元组(Q,∑, 定义2(服务弱形式化模型)2!给定一个服务 6,,),其中?是一个有穷集合,叫做状态集:∑ e-Service,则e-Service可以表示为一个有限状态自 是一个有穷集合,叫做字母表:6:Q×∑Q是转移 动机FSA,并且FSA是一个六元组(Q,1,O,6, 函数;φ∈Q是起始状态;F二Q是接收状态集 仰,可,其中Q是一个有穷集合,是FSA的状态集, e-Service可以看成是一个软件“黑箱”,它可以 其中状态表示客户与e-Service交互序列中的历史 与客户交互,包括3步:1)客户通过发送输入命令 记录:I是输入命令input-command的有穷集合 (input-command)调用e-Service;2)输入命令激发 O是输出消息output-message的有穷集合,IXO e-Service的内部计算(internal-computation);3) 是FSA的字母表:6:QX1×O→Q是转移函数,即 客户得到e-Service的输出消息(output-mes 给定一个状态,根据<input-command,output. sage).因此,e-Service交互可以用3元组<input- message>,FSA能够转移到另一个状态;∈Q是 command,internal-computation,output-mes- 起始状态;F∈Q是接收状态集,即用户能够与e sage>表示.由于采用“黑箱”的方法,交互可用二元 Service结束交互的状态集, 组<input-command,output-message>来表示. 图1是一个基于有限状态自动机的股票交易服 因而可用有限状态自动机来描述e-Service,即 务2 e-Service的每次交互可以看成是有限状态自动机 buy/displayedResults userData/checkedAccount continue/displayedStock Data stop/emailNotification userData/not ValidClient sell/displayedResults 图1股票交易服务 Fig.1 Stock service 股票交易服务的形式化模型可以定义为 定义3(命题逻辑公式)命题逻辑公式按下列 FSA=(Q,1,O,6,m,F),其中状态集Q= 规则生成: {o,s1,s,s3,4};输入命令集合I=fuserData, 1)常量true和false是命题逻辑公式: continue,buy,sel,stop},输出消息集合O= 2)命题变元是命题逻辑公式: /checkedAccount,notValidClient,displayedStock- 3)如果中是命题逻辑公式,则中也是命题逻辑 Data,displayedResults,emailNotification,字母表 公式: IXO =f userData/checkedAccount,userData/ 4如果中和μ是命题逻辑公式,则中“和中V not ValidClient,continue/displayedStockData, μ也是命题逻辑公式: buy/displayedResults,sell/displayedResults, 5)命题逻辑公式只能由上述规则生成: stop/emailNotification以,转移函数6为:0 Xuser 定义4(条件)条件是由状态和命题逻辑公式 Data/checkedAccount -si,so X userData/ 通过联结词组成的表达式,形式定义如下: not ValidClient-s4,s Xcontinue/displayedStock- 假设Q是有限状态自动机状态的集合,E是命 Data-s2,s2 Xbuy/displayedResults -s2.s2 Xsell/ 题逻辑公式的集合,or和and是条件联结词,则条 displayedResults -s2,s Xstop/emailNotification 件按下列规则生成: ;0∈Q是起始状态,接收状态集F={g,4}. l)p、q∈Q,则porq和p and g是条件: 服务组合是根据组合算子来实现的,而有些组 2)p∈Q,e∈E,则p and e是条件(如果e= 合算子(如If-Them Else算子)涉及到条件,因而需 true,则简写为pl: 要一种新的自动机的定义 3)如果a和a是条件,则a and a和aora 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
出一些基本概念. 定义 1 (有限状态自动机) 有限状态自动机 (finite state automata , FSA) 是一个五元组( Q , ∑, δ, q0 , F) ,其中 Q 是一个有穷集合 ,叫做状态集; ∑ 是一个有穷集合 ,叫做字母表;δ: Q ×∑→Q是转移 函数; q0 ∈Q 是起始状态; F ΑQ 是接收状态集. e2Service 可以看成是一个软件“黑箱”,它可以 与客户交互 ,包括 3 步 :1) 客户通过发送输入命令 (inp ut command) 调用 e2Service ;2) 输入命令激发 e2Service 的内部计算 (internal comp utation) ; 3) 客户 得到 e2Service 的输出消 息 ( outp ut mes2 sage) . 因此 ,e2Service 交互可以用 3 元组 < inp ut command , internal comp utation , outp ut mes2 sage > 表示. 由于采用“黑箱”的方法 ,交互可用二元 组 < inp ut command , outp ut message > 来表示. 因而可用有限状态自动机来描述 e2Service ,即 e2Service 的每次交互可以看成是有限状态自动机 的状态转换 ,并且交互可用二元组 < inp ut com2 mand , outp ut message > 来表示. 定义 2 (服务弱形式化模型) [12 ] 给定一个服务 e2Service ,则 e2Service 可以表示为一个有限状态自 动机 FSA ,并且 FSA 是一个六元组 ( Q , I , O , δ, q0 , F) ,其中 Q 是一个有穷集合 ,是 FSA 的状态集 , 其中状态表示客户与 e2Service 交互序列中的历史 记录; I 是输入命令 inp ut command 的有穷集合; O 是输出消息 outp ut message 的有穷集合 , I ×O 是 FSA 的字母表;δ: Q ×I ×O →Q 是转移函数 ,即 给定一个状态 , 根据 < inp ut command , outp ut _ message > ,FSA 能够转移到另一个状态; q0 ∈Q 是 起始状态; F Α Q 是接收状态集 , 即用户能够与 e2 Service 结束交互的状态集. 图 1 是一个基于有限状态自动机的股票交易服 务[12 ] . 图 1 股票交易服务 Fig. 1 Stock service 股票交易服务的形式化模型可以定义为 FSA = ( Q , I , O , δ, s0 , F) ,其中状态集 Q = { s0 , s1 , s2 , s3 , s4 } ;输入命令集合 I = { userData , continue , buy , sell , stop } , 输出消 息集合 O = { checkedAccount , notValidClient , displayedStock2 Data , displayedResults , emailNotification} ,字母表 I ×O = { userData/ checkedAccount , userData/ notValidClient , continue/ displayedStockData , buy/ displayedResults , sell/ displayedResults , stop/ emailNotification} ; 转移函数δ为 : s0 ×user2 Data/ checkedAccount → s1 , s0 × userData/ notValidClient →s4 , s1 ×continue/ displayedStock2 Data →s2 , s2 ×buy/ displayedResults →s2 , s2 ×sell/ displayedResults →s2 , s2 ×stop/ emailNotification →s3 ;s0 ∈Q 是起始状态;接收状态集 F = { s3 ,s4 } . 服务组合是根据组合算子来实现的 ,而有些组 合算子(如 If2Then2Else 算子) 涉及到条件 ,因而需 要一种新的自动机的定义. 定义 3 (命题逻辑公式) 命题逻辑公式按下列 规则生成 : 1) 常量 true 和 false 是命题逻辑公式 ; 2) 命题变元是命题逻辑公式 ; 3) 如果φ是命题逻辑公式 ,则┓φ也是命题逻辑 公式; 4) 如果φ和μ是命题逻辑公式 ,则φ∧μ和φ∨ μ也是命题逻辑公式; 5) 命题逻辑公式只能由上述规则生成. 定义 4 (条件) 条件是由状态和命题逻辑公式 通过联结词组成的表达式 ,形式定义如下 : 假设 Q 是有限状态自动机状态的集合 , E 是命 题逻辑公式的集合 ,or 和 and 是条件联结词 ,则条 件按下列规则生成 : 1) p、q ∈Q ,则 p or q 和 p and q 是条件; 2) p ∈Q , e ∈E, 则 p and e 是条件 (如果 e = true ,则简写为 p) ; 3) 如果 c1 和 c2 是条件 ,则 c1 and c2 和 c1 or c2 第 2 期 蒋运承 ,等 :基于有限状态自动机的服务组合模型 · 94 ·

·50· 智能系统学报 第1卷 也是条件; e-Service结束交互的状态集;QC:QXC是状态的条 4)条件只能由上述规则生成: 件集 条件的语义解释是:条件porq表示状态p和 图2是一个基于带条件的有限状态自动机的旅 g只选择一个;条件p and g表示状态p,g都选择: 游购票服务,定义为: 条件p and e表示当e的值为真时才选择状态p;对 cFSA=(Q,1,O,6,m,F,QCg,其中状态集Q= 于复杂条件a and c和aora类似进行解释. 0,n,2,3,y,s,6,}:输入命令集合I=fuser- 定义5(带条件的有限状态自动机)带条件的 Data,continue,buy,stop},输出消息集合O= 有限状态自动机(inite state automata with condi- checkedAccount,notValidClient,displayed Ticket tion,cFSA)是一个六元组(Q,∑,6,,F,Qg,其 -Data,displayedResults,emailNotification, 中Q是一个有穷集合,叫做状态集;Σ是一个有穷 IXO={userData/checkedAccount,userData/ 集合,叫做字母表,6:Q×∑×QC→Q是转移函数: not Valid -Client,continue/displayed TicketData, p∈Q是起始状态;FSQ是接收状态集;QC:Q×C buy/displayed -Results,stop/emailNotification: 是状态的条件集 转移函数6为:so XuserData/checkedAccount Xha- 定义6(服务形式化模型)给定一个服务 sAir Ticket -st,so XuserData/checkedAccount X e-Service,则e-Service可以表示为一个带条件的有hasAir Ticket,so XuserData/not ValidClient X 限状态自动机cFSA,并且cFSA是一个七元组(g,true→s,s X continue/displayedStockData X I,O,6,m,F,QCg,其中Q是一个有穷集合,是true,Xbuy/displayed-Results Xtrue→4, cFSA的状态集,其中状态表示客户与e-Service交 ss Xbuy/displayedResults Xtrue -ss,s X stop/ 互序列中的历史记录或条件判断记录:1是输入命 emailNotification Xtrue -s6.ss Xstop/emailNotifi- 令input-command的有穷集合,O是输出消息 cation Xtrue→;so∈Q是起始状态;接收状态集 output-message的有穷集合,IXO是cFSA的字 F={3,%,5}:状态条件集QC是:状态So的条件 母表;6:Q×1X0×QC→Q是转移函数,即给定一 S and hasAir Ticket or S2 and 个状态,根据<input-command,output-message> hasAir Ticket)orS,状态s,2,s4,s的条件都 和条件,cFSA可以转移到另一个或几个状态;∈ 是true,而s3,%,m没有带条件. Q是起始状态;F三Q是接收状态集,即用户能够与 (s and hasAirTicket)or(s:and-hasAirTicket)or s; buy/displayedResults continue/displayedTicketData stop/emailNotification userData/checkedAccount userData/checkedAccount continue/displayedTicketData stop/emailNotification user Data/not ValidClient buy/displayedResults 图2旅游购票服务 Fig.2 Travel book service 2服务组合模型 fs455,输入命令集s=fos,s …is/,输出消息集0s=f0505,5/,字 2.1 简单结构的服务组合模型 母表10s,=fim5ios5,ios,转移函数 假设服务eS.的形式化模型cFSAes,=(Qs, =1④s,④5,8,接收状态集F=f55, es,0s,④,Sos,F,Cs),其中状态集Qs= ss},状态条件集QCs为:ss∈Qs八s年 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
也是条件; 4) 条件只能由上述规则生成. 条件的语义解释是 :条件 p or q 表示状态 p 和 q 只选择一个;条件 p and q 表示状态 p , q 都选择; 条件 p and e 表示当 e 的值为真时才选择状态 p ;对 于复杂条件 c1 and c2 和 c1 or c2 类似进行解释. 定义 5 (带条件的有限状态自动机) 带条件的 有限状态自动机 (finite state automata wit h condi2 tion , cFSA) 是一个六元组 ( Q , ∑,δ, q0 , F, QC) ,其 中 Q 是一个有穷集合 ,叫做状态集; ∑是一个有穷 集合 ,叫做字母表;δ: Q ×∑×QC →Q 是转移函数; q0 ∈Q 是起始状态; F Α Q 是接收状态集; QC: Q ×C 是状态的条件集. 定义 6 (服务形式化模型) 给定一个服务 e2Service ,则 e2Service 可以表示为一个带条件的有 限状态自动机 cFSA , 并且 cFSA 是一个七元组( Q , I , O ,δ, q0 , F, QC) , 其中 Q 是一个有穷集合 , 是 cFSA的状态集 ,其中状态表示客户与 e2Service 交 互序列中的历史记录或条件判断记录; I 是输入命 令 inp ut command 的有穷集合 , O 是输出消息 outp ut message 的有穷集合 , I ×O 是 cFSA 的字 母表;δ: Q ×I ×O ×QC →Q 是转移函数 ,即给定一 个状态 ,根据 < input command , output message > 和条件 ,cFSA 可以转移到另一个或几个状态 ; q0 ∈ Q 是起始状态; F ΑQ 是接收状态集 ,即用户能够与 e2Service 结束交互的状态集 ; QC:Q ×C 是状态的条 件集. 图 2 是一个基于带条件的有限状态自动机的旅 游购票服务 ,定义为 : cFSA = ( Q , I , O ,δ,s0 , F, QC) ,其中状态集Q = { s0 ,s1 ,s2 ,s3 ,s4 ,s5 ,s6 , s7 } ;输入命令集合 I = { user2 Data , continue , buy , stop } , 输出消息集合 O = {checkedAccount , notValidClient , displayedTicket 2Data , displayedResults , emailNotification} , 字母 表 I ×O = { userData/ checkedAccount , userData/ notValid 2Client , continue/ displayedTicketData , buy/ displayed 2Results , stop/ emailNotification } ; 转移函数δ为 :s0 ×userData/ checkedAccount ×ha2 sAir Ticket →s1 , s0 ×userData/ checkedAccount × ┓ hasAir Ticket →s2 , s0 ×userData/ notValidClient × true →s3 , s1 ×continue/ displayedStockData × true →s4 , s4 ×buy/ displayed 2Results ×true →s4 , s5 ×buy/ displayedResults ×true →s5 , s4 × stop/ emailNotification ×true →s6 , s5 ×stop/ emailNotifi2 cation ×true →s7 ; s0 ∈Q 是起始状态; 接收状态集 F = { s3 ,s6 ,s7 } ;状态条件集 QC 是 :状态 S0 的条件 是 ( S1 and hasAir Ticket ) or ( S2 and ┓ hasAir Ticket) or S3 ,状态 s1 , s2 , s4 , s5 的条件都 是 true ,而 s3 , s6 , s7 没有带条件. 图 2 旅游购票服务 Fig. 2 Travel book service 2 服务组合模型 2. 1 简单结构的服务组合模型 假设服务 eSi 的形式化模型 c FS AeS i = ( QeS i , IeS i , OeS i ,δeS i , S0 eS i , FeS i , QCeS i ) , 其中状态集 QeS i = { s0 eS i ,s1 eS i , …, sn eS i } , 输入命令集 IeS i = { i0 eS i , i1 eS i , …, imeS i } ,输出消息集 OeS i = { o0 eS i , o1 eS i , …, ok eS i } ,字 母表 IeS i ×OeS i = { io0 eS i , io1 eS i , …, iot eS i } , 转移函数 δeS i = {δ0 eS i ,δ1 eS i , …,δh eS i } ,接收状态集 FeS i = { su eS i , …,sv eS i } ,状态条件集 QCeS i 为 : Πsi eS i ∈QeS i ∧si eS i | · 05 · 智 能 系 统 学 报 第 1 卷
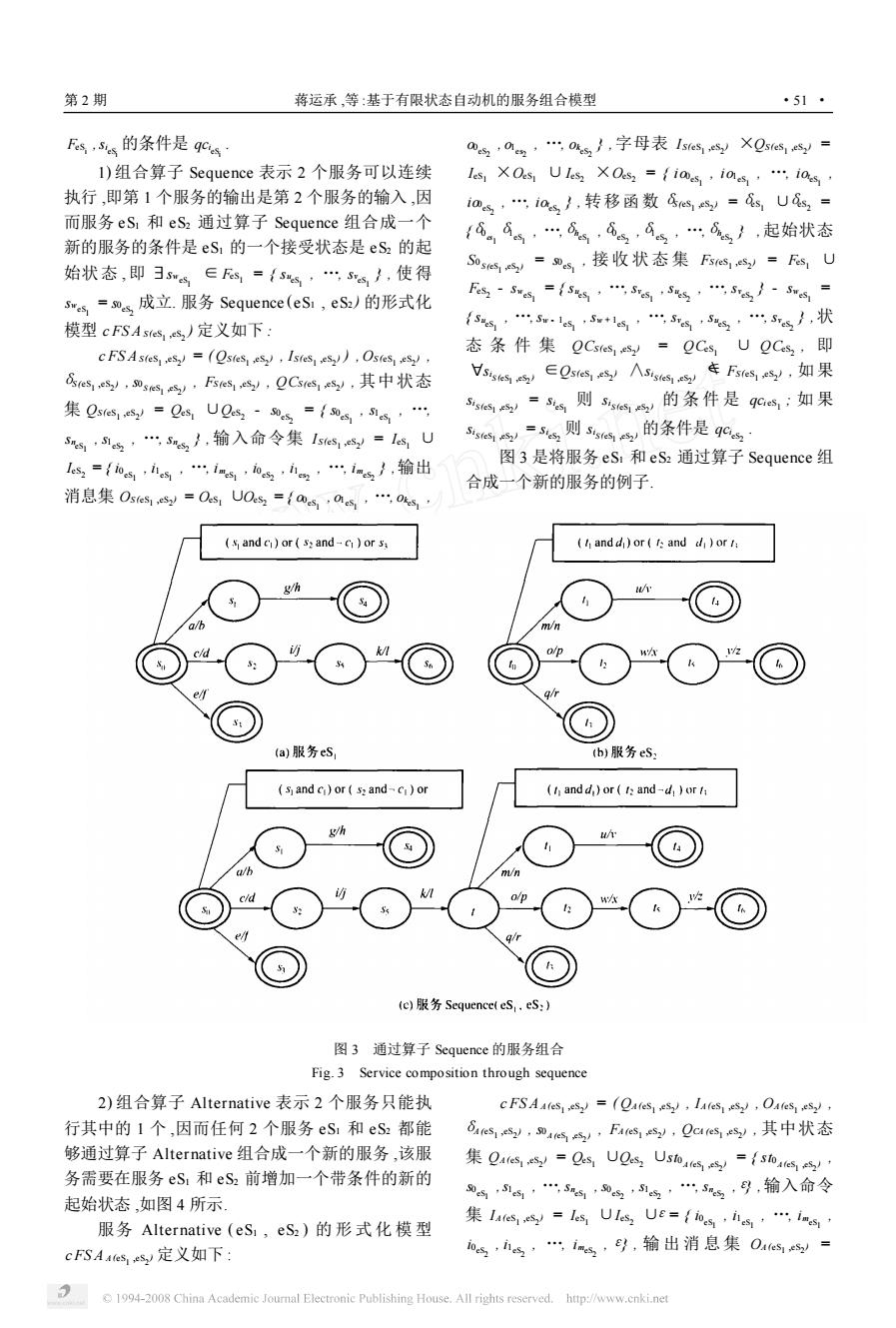
第2期 蒋运承,等:基于有限状态自动机的服务组合模型 ·51· Fs,5s的条件是qCs 0ms,0,0%},字母表1ses,es XOstes1sy= 1)组合算子Sequence表示2个服务可以连续 les XOes Ules XOes2 =(ias ioes,ioes, 执行,即第1个服务的输出是第2个服务的输入,因 i0,i0s,转移函数④s=,U,= 而服务eS,和eS,通过算子Sequence组合成一个 1④。,8,,4,…8s},起始状态 新的服务的条件是eS,的一个接受状态是eS的起 始状态,即3ss∈F=(5,5s/,使得 S0s=6,接收状态集Fs=F,U ss=0s成立.服务Sequence(eS,eSa)的形式化 F5mes=f%,5s,5线’5-5es= 模型cFSAstes,)定义如下: …55*1”55气…55,状 CFS Astes)=(Ostes e)Istes)),Ostes), 态条件集QCe,y=QCs,UQCs,即 &es,0ss,F压e,QCss,其中状态 s6∈sesy八sge年Fs,如果 集0sesy=0sU0s则5={sss,” 5的=s则ss的条件是9G;如果 5,5},输入命令集1 ste5:53=1s,U 5s=5s则ss的条件是g95 ls,={osh,i的0i,…i线,输出 图3是将服务eS!和eS通过算子Sequence组 合成一个新的服务的例子 消息集O5e1=0s1U0s={0s,0s,”01 (s and c)or s:and-c)or s (h andd)or (t:and d or h 访 o/p e 9 (a)服务eS b)服务eS: (s and ci)or s2 and-c)or (1 and d,)or I:and-d)or h a/b o/p (e)服务Sequence(eS,es:) 图3通过算子Sequence的服务组合 Fig.3 Service composition through sequence 2)组合算子Alternative表示2个服务只能执 cFSAA(eS)=(Qa(es )IAfeS,Oafes) 行其中的1个,因而任何2个服务eS和eS:都能 es,0es,Bs,Qes,其中状态 够通过算子Alternative组合成一个新的服务,该服 Qates5)=Qes:UQes:Usto tes(stotes 务需要在服务eS:和eS2前增加一个带条件的新的 起始状态,如图4所示. 4,”55,…55,号,输入命令 服务Alternative(eS,eS,)的形式化模型 集1es=sUls,Ue=fo线,s,…is cFSA4es,y定义如下: shs,is,y,输出消息集Os= 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
FeS i ,si eS i 的条件是 qci eS i . 1) 组合算子 Sequence 表示 2 个服务可以连续 执行 ,即第 1 个服务的输出是第 2 个服务的输入 ,因 而服务 eS1 和 eS2 通过算子 Sequence 组合成一个 新的服务的条件是 eS1 的一个接受状态是 eS2 的起 始状态 , 即 ϖsweS 1 ∈FeS 1 = { su eS 1 , …, sv eS 1 } , 使得 sweS 1 = s0 eS 2 成立. 服务 Sequence (eS1 , eS2 ) 的形式化 模型 c FS A S (eS 1 ,eS 2 ) 定义如下 : c FS A S (eS 1 ,eS 2 ) = ( QS (eS 1 ,eS 2 ) , IS (eS 1 ,eS 2 ) ) , OS (eS 1 ,eS 2 ) , δS (eS 1 ,eS 2 ) , s0 S (eS 1 ,eS 2 ) , FS (eS 1 ,eS 2 ) , QCS (eS 1 ,eS 2 ) , 其中状态 集 QS (eS 1 ,eS 2 ) = QeS 1 ∪QeS 2 - s0 eS 2 = { s0 eS 1 , s1 eS 1 , …, sn eS 1 , s1 eS 2 , …, sn eS 2 } , 输入命令集 IS (eS 1 ,eS 2 ) = IeS 1 ∪ IeS 2 = { i0 eS 1 , i1 eS 1 , …, imeS 1 , i0 eS 2 , i1 es 2 , …, imeS 2 } ,输出 消息集 OS (eS 1 ,eS 2 ) = OeS 1 ∪OeS 2 = { o0 eS 1 , o1 eS 1 , …, ok eS 1 , o0 eS 2 , o1 es 2 , …, ok eS 2 } , 字母表 IS (eS 1 ,eS 2 ) ×QS (eS 1 ,eS 2 ) = IeS 1 ×OeS 1 ∪IeS 2 ×OeS 2 = { io0 eS 1 , io1 eS 1 , …, iot eS 1 , io0 eS 2 , …, iot eS 2 } , 转移函数 δS (eS 1 ,eS 2 ) =δeS 1 ∪δeS 2 = {δ0 es 1 δ1 eS 1 , …,δh eS 1 ,δ0 eS 2 ,δ1 eS 2 , …,δh eS 2 } , 起始状态 S0 S (eS 1 ,eS 2 ) = s0 eS 1 , 接 收 状 态 集 FS (eS 1 ,eS 2 ) = FeS 1 ∪ FeS 2 - sweS 1 = { su eS 1 , …, sv eS 1 , su eS 2 , …, sv eS 2 } - sweS 1 = { su eS 1 , …,sw - 1 eS 1 , sw + 1 eS 1 , …, sv eS 1 , su eS 2 , …, sv eS 2 } ,状 态 条 件 集 QCS (eS 1 ,eS 2 ) = QCeS 1 ∪ QCeS 2 , 即 Πsi S (eS 1 ,eS 2 ) ∈QS (eS 1 ,eS 2 ) ∧si S (eS 1 ,eS 2 ) | FS (eS 1 ,eS 2 ) , 如果 si S (eS 1 ,eS 2 ) = si eS 1 则 si S (eS 1 ,eS 2 ) 的 条 件 是 qci eS 1 ; 如 果 si S (eS 1 ,eS 2 ) = si eS 2 则 si S (eS 1 ,eS 2 ) 的条件是 qci eS 2 . 图 3 是将服务 eS1 和 eS2 通过算子 Sequence 组 合成一个新的服务的例子. 图 3 通过算子 Sequence 的服务组合 Fig. 3 Service composition through sequence 2) 组合算子 Alternative 表示 2 个服务只能执 行其中的 1 个 ,因而任何 2 个服务 eS1 和 eS2 都能 够通过算子 Alternative 组合成一个新的服务 ,该服 务需要在服务 eS1 和 eS2 前增加一个带条件的新的 起始状态 ,如图 4 所示. 服务 Alternative ( eS1 , eS2 ) 的 形 式 化 模 型 c FS A A (eS 1 ,eS 2 ) 定义如下 : c FS A A (eS 1 ,eS 2 ) = ( QA (eS 1 ,eS 2 ) , IA (eS 1 ,eS 2 ) , OA (eS 1 ,eS 2 ) , δA (eS 1 ,eS 2 ) , s0 A (eS 1 ,eS 2 ) , FA (eS 1 ,eS 2 ) , QCA (eS 1 ,eS 2 ) , 其中状态 集 QA (eS 1 ,eS 2 ) = QeS 1 ∪QeS 2 ∪st0 A (eS 1 ,eS 2 ) = { st0 A (eS 1 ,eS 2 ) , s0 eS 1 ,s1 eS 1 , …, sn eS 1 , s0 eS 2 , s1 eS 2 , …, sn eS 2 ,ε} ,输入命令 集 IA (eS 1 ,eS 2 ) = IeS 1 ∪IeS 2 ∪ε= { i0 eS 1 , i1 eS 1 , …, imeS 1 , i0 eS 2 , i1 eS 2 , …, imeS 2 ,ε} , 输 出 消 息 集 OA (eS 1 ,eS 2 ) = 第 2 期 蒋运承 ,等 :基于有限状态自动机的服务组合模型 · 15 ·

·52· 智能系统学报 第1卷 服务Choice(eS,…,eS.)的形式化模型 CFS A cMes,,es)定义如下: cFSA cles,=(Qates,,Icfes,, Oatess,ates Fares Soates ACavtes,esy其中状态集Qaes,“e=Q,UU Qs.Ushates,5=(stoaless5 5的,6,6。,s,输入命令集1a,= 图4通过算子Alternative的服务组合 Ies U.U les Ue=f ios 1,ites imes toes Fig.4 Service composition through alternative 45,…ia,号,输出消息集0aes,5=0,U as Uos,Ue=faso.os UOes,Ue=(o 0,,字母表1 stes XOsts Uf=es,X 0s,,字母表1aesX0aeU{= Oes Ulesz XOs:U!gg=(ias ias ioes les XOes U...U Ies,XOs,Ufee =ias ios i0sio6:io,9g,转移函数s=④U i0,ioms,i0es.,i0s,,转移函数 s,U{s面,xqe Xtrue%s5面65X Bales.s=ds U...uos.Uf shates,m xex erue0s}=(④s,s,6,, true→s,”sha6s,sXqe Xtrue→s,}= A3面es,X6 Xtrue5面e5X9eX ④,4,…,4,…85s true→/,起始状态为s面,5,接收状态集 ge Xtrue一s,”5hales,xge Xtrue→ FAe)=Fs UFes =f smes Sves s ,,起始状态为s和,,接收状态集 s/,状态条件集QCe=ocs,Uoas,U Fates5)Fes U..U Fs,=(sxes.Stes, (orms,即s∈QyΛs年 ss,5s,,状态条件集QCals=QCsU Bes,如果s=6则5s的条件是 uocs U(andand or q心:如果=5则s的条件是 and.and s.s,). 4)组合算子Condition表示只有满足一定的条 qcs如果=5而s,则s的条件是 件才执行某个服务,因而服务Condition(中,eS)需 (Ss,0r50s. 要增加1个带条件的新的起始状态,如图6所示, 3)组合算子Choice是组合算子Alternative的 推广,算子Choice表示从n个服务中选择m个服务 执行(m≤n).因而服务Choice(m,n,eS,…,eSn) (简写为Choice(eS,…,eS.)需要增加一个带条 件的新的起始状态,如图5所示。 (Sp and..and s) or ...or 图6通过算子Condition的服务组合 (and..and Su) Fig.6 Service composition through condition 服务Condition(中,es)的形式化模型 CFSAard.es定义如下: CFSAco(t.es (Ocord.es)Icord.es,Ocord.es), fey,Faey,oey,QColt.),其中状态集 Qolt.e Qes Usate =(ar5ts .Sres 输入命令集1ay=1sUe={ios,is,”ims,号, 图5通过算子Choice的服务组合 输出消息集Oaey=OsUe={os,0s,”0ms Fig.5 Service composition through Choice 号,字母表1 rt.es XOcrd.es U{号=Ies XOesL{ 号={i0s,i0s,i0s,以,转移函数as= 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved.http://www.cnki.net
图 4 通过算子 Alternative 的服务组合 Fig. 4 Service composition through alternative OeS 1 ∪OeS 2 ∪ε= { o0 eS 1 , o1 eS 1 , …, ok eS 1 , o0 eS 2 , o1 eS 2 , …, ok eS 2 ,ε} ,字母表 IS (eS 1 ,eS 2 ) ×QS (eS 1 ,eS 2 ) ∪{ε/ε} = IeS 1 × OeS 1 ∪IeS 2 ×OeS 2 ∪{ε/ε} = { io0 eS 1 , io1 eS 1 , …, iot eS 1 , io0 eS 2 , io1 eS 2 , …, iot eS 2 ,ε/ε} ,转移函数δA(eS 1 ,eS 2 ) =δeS 1 ∪ δeS 2 ∪{ st0 A (eS 1 ,eS 2 ) ×ε/ε×true →s0 eS 1 , st0 A (eS 1 ,eS 2 ) ×ε/ ε×true →s0 eS 2 } = {δ0 eS 1 ,δ1 eS 1 , …,δh eS 2 ,δ0 eS 2 ,δ1 eS 2 , …, δh eS 2 ,st0 A (eS 1 , eS 2 ) ×ε/ε×true →s0 eS 1 , st0 A (eS 1 ,eS 2 ) ×ε/ε× true →s0 eS 2 } , 起始状态为 st0 A (eS 1 , eS 2 ) , 接收状态集 FA (eS 1 , eS 2 ) = FeS 1 ∪FeS 2 = { su eS 1 , …, sv eS 1 , su eS 2 , …, sv eS 2 } , 状态条件集 QCA (eS 1 ,eS 2 ) = QCeS 1 ∪QCeS 2 ∪ (s0 eS 1 or s0 eS 2 ) ,即 Πsi A (eS 1 ,eS 2 ) ∈QA (eS 1 ,eS 2 ) ∧si A (eS 1 ,eS 2 ) | FA (eS 1 ,eS 2 ) ,如果 si A (eS 1 ,eS 2 ) = si eS 1 则 si A (eS 1 ,eS 2 ) 的条件是 qci eS 1 ; 如 果 si A (eS 1 ,eS 2 ) = si eS 2 则 si A (eS 1 ,eS 2 ) 的 条 件 是 qci eS 2 ;如果 si A (eS 1 ,eS 2 ) = st0 A (eS 1 ,eS 2 ) 则 si A (eS 1 ,eS 2 ) 的条件是 (s0 eS 1 or s0 eS 2 ) . 3) 组合算子 Choice 是组合算子 Alternative 的 推广 ,算子 Choice 表示从 n 个服务中选择 m 个服务 执行( m ≤n) . 因而服务 Choice ( m , n , eS1 , …,eSn ) (简写为 Choice (eS1 , …,eSn ) ) 需要增加一个带条 件的新的起始状态 ,如图 5 所示. 图 5 通过算子 Choice 的服务组合 Fig. 5 Service composition through Choice 服务 Choice ( eS1 , …, eSn ) 的 形 式 化 模 型 c FS A Ch (eS 1 , …,eS n ) 定义如下 : c FS A Ch (eS 1 , …,eS n ) = ( QCh (eS 1 , …,eS n ) , ICh (eS 1 , …,eS n ) , OCh (eS 1 , …,eS n ) ,δCh (eS 1 , …,eS n ) , FCh (eS 1 , …,eS n ) , S0Ch (eS 1 , …,eS n ) , A CCh (eS 1 , …,eS n ) 其中状态集 QCh (eS 1 , …,eS n ) = QeS 1 ∪…∪ QeS n ∪st0 Ch (eS 1 , …,eS n ) = { st0 Ch (eS 1 , …,eS n ) , s0 eS 1 , s1 eS 1 , …, sn eS 1 , …,s0 eS n ,s1 eS n , …,sn eS n } ,输入命令集 ICh(eS 1 , …,eS n ) = IeS 1 ∪…∪IeS n ∪ε= { i0 eS 1 } , i1 eS 1 …, imeS 1 , …, i0 eS 1 , i1 eS 1 , …, imeS 1 n ,ε} ,输出消息集 OCh (eS 1 , …,eS n ) = OeS 1 ∪ …∪OeS n ∪ε= { o0 eS 1 , o1 eS 1 , …, omeS 1 , …, o0 eS n , o1 eS n , …, omeS n ,ε} ,字母表 ICh(eS 1 , …,eS n ) ×OCh (eS 1 , …,eS n ) ∪{ε/ε} = IeS 1 ×OeS 1 ∪…∪IeS n ×OeS n ∪{ε/ε} = { io0 eS 1 , io1 eS 1 , …, iot eS 1 , …, io0 eS n , io1 eS n , …, iot eS n ,ε/ε} , 转移函数 δCh (eS 1 , …,eS n ) =δeS 1 ∪…∪δeS n ∪{ st0 Ch (eS 1 , …,eS n ) ×ε/ε× true →s0 eS 1 , …, st0 Ch (eS 1 , …,eS n ) ×ε/ε×true →s0 eS n } = {δ0 eS 1 ,δ1 eS 1 , …,δh eS 2 ,δ0 eS 2 ,δ1 eS 2 , …,δh eS 2 ,st0 A (eS 1 ,eS 2 ) × ε/ε×true →s0 eS 1 , …, st0 Ch (eS 1 , …,eS n ) ×ε/ε×true → s0 eS n } , 起 始 状 态 为 st0 Ch (eS 1 , …,eS n ) , 接 收 状 态 集 FCh (eS 1 ,eS 2 ) = FeS 1 ∪…∪FeS n = { su eS 1 , …, sv eS 1 , …, su eS n , …, sv eS n } ,状态条件集 QCCh (eS 1 , …,eS n ) = QCeS 1 ∪ …∪QCeS n ∪( (s0 eS 1 , and …and s0 eSm ) or …or (s0 eS( n - m) and …and s0 eS n ) ) . 4) 组合算子 Condition 表示只有满足一定的条 件才执行某个服务 ,因而服务 Condition (φ,eS) 需 要增加 1 个带条件的新的起始状态 ,如图 6 所示. 图 6 通过算子 Condition 的服务组合 Fig. 6 Service composition through condition 服 务 Condition (φ, eS) 的 形 式 化 模 型 c FS A Co(φ, eS) 定义如下 : c FS A Co(φ,eS) = ( QCo(φ,eS) , ICo(φ,eS) , OCo(φ,eS) , δCo(φ,eS) , FCo(φ,eS) , s0 Co(φ,eS) , QCCo(φ,eS) ) , 其 中 状 态 集 QCo(φ,eS) = QeS ∪s0 Co(φ,eS) = { s0 Co(φ,eS) , s0 eS , s1 eS , …, sn eS } , 输入命令集 ICo(φ,eS) = IeS ∪ε= { i0 eS , i1 eS , …, imeS ,ε} , 输出消息集 OCo(φ, eS) = OeS ∪ε= { o0 eS , o1 eS , …, omeS , ε} ,字母表 ICo(φ,eS) ×OCo(φ, eS) ∪{ε/ε} = IeS ×OeS ∪{ε/ ε} = { io0 eS , io1 eS , …, iot eS ,ε/ε} , 转移函数δCo(φ,eS) = · 25 · 智 能 系 统 学 报 第 1 卷