
160 翁译原理及实践 China-pub.Co 下载 表5-4例5.9中的文法的分析表 状态 动作 规则 输入 Goto 0 4-A 2 归约 A-a 3 移进 移进 归约 A-(A) 在这样的分析表中的空白项表示的是错误。当必须要进行错误恢复时,则需要准确地指出 分析程序要为每个这些空白项采取什么动作。后面一节将讨论这个问题。 5.3SLR(1)分析 5.3.1SLR(1)分析算法 简单LR(I)分析,或SLR(I)分析,也如上一节中一样使用了LR(O)项目集合的DFA。但是 通过使用输入串中下一个记号来指导它的动作,它大大地提高了LR(O)分析的能力。它通过两 种方法做到这一点。首先,它在一个移进之前先考虑输入记号以确保存在着一个恰当的DFA 其次,它使用如4.3节所构造的非终结符的Foow集合来决定是否应执行一个归约。令人吃惊 的是,先行的这个简单应用的能力强大得足以分析几乎所有的一般的语言构造。 定义:SLR(I)分析算法(SLR(I)parsing algorithm)。令s为当前状态(位于分析栈的顶 部)。则动作可定义如下: 1.若状态s包含了格式A一Q.邓的任意项目,其中X是一个终结符,且X是输入串 中的下一个记号,则动作将当前的输入记号移进到栈中,且被压入到栈中的新 状态是包含了项目A一XB的状态 2.若状态s包含了完整项目A一Y.,则输入串中的下一个记号是在Follow(4)中,所 以动作是用规则A→y归约。用规则S→S归约与接受等价,其中S是开始状态: 只有当下一个输入记号是$时,这才会发生⊙。在所有的其他情况中,新状态都 是如下计算的:别除串α和所有它的来自分析栈中的对应状态。相对应地, DFA回到α开始构造的状态。通过构造,这个状态必须包括格式B一Y.AB的 个项目。将A压入到栈中,并将包含了项目B一aA.B的状态压入。 3.若下一个输入记号都不是上面两种情况所提到的,则声明一个错误 若上述的SLR(I)分析规则并不导致二义性,则文法为SLR()文法(SLR(I)grammar)。特别 地,当且仅当对于任何状态5,以下的两个条件: I)对于在s中的任何项目A一a邓,当X是一个终结符,且X在Follow(B)中时,s中没有完 整的项目B→y,。 2)对于在s中的任何两个完整项目A→a.和B→B,Follow(A)Follow(B)为空。 。实际上,任何文法扩充的开始状态了的Fow集合总是只由S组成,这是因为S只出现在文法规则S一S中
表5-4 例5 . 9中的文法的分析表 状 态 动 作 规 则 输 入 G o t o ( a ) A 0 移进 3 2 1 1 归约 A¢→ A 2 归约 A→ a 3 移进 3 2 4 4 移进 5 5 归约 A→ ( A ) 在这样的分析表中的空白项表示的是错误。当必须要进行错误恢复时,则需要准确地指出 分析程序要为每个这些空白项采取什么动作。后面一节将讨论这个问题。 5.3 SLR(1)分析 5.3.1 SLR(1)分析算法 简单L R ( 1 )分析,或S L R ( 1 )分析,也如上一节中一样使用了 L R ( 0 )项目集合的D FA。但是, 通过使用输入串中下一个记号来指导它的动作,它大大地提高了 L R ( 0 )分析的能力。它通过两 种方法做到这一点。首先,它在一个移进之前先考虑输入记号以确保存在着一个恰当的 D FA。 其次,它使用如 4 . 3节所构造的非终结符的 F o l l o w集合来决定是否应执行一个归约。令人吃惊 的是,先行的这个简单应用的能力强大得足以分析几乎所有的一般的语言构造。 定义:S L R ( 1 )分析算法(SLR(1) parsing algorithm)。令s 为当前状态(位于分析栈的顶 部)。则动作可定义如下: 1. 若状态s 包含了格式A→a.Xb的任意项目,其中X是一个终结符,且X是输入串 中的下一个记号,则动作将当前的输入记号移进到栈中,且被压入到栈中的新 状态是包含了项目A→aX.b的状态。 2. 若状态s 包含了完整项目A→g.,则输入串中的下一个记号是在F o l l o w (A)中,所 以动作是用规则A→g 归约。用规则S¢→S归约与接受等价,其中S是开始状态; 只有当下一个输入记号是 $时,这才会发生 。在所有的其他情况中,新状态都 是如下计算的:删除串 a和所有它的来自分析栈中的对应状态。相对应地, D FA回到a开始构造的状态。通过构造,这个状态必须包括格式 B→g. Ab的一 个项目。将A压入到栈中,并将包含了项目B→aA.b的状态压入。 3. 若下一个输入记号都不是上面两种情况所提到的,则声明一个错误。 若上述的S L R ( 1 )分析规则并不导致二义性,则文法为 S L R ( 1 )文法(SLR(1) grammar)。特别 地,当且仅当对于任何状态s,以下的两个条件: 1) 对于在s 中的任何项目A→a.Xb,当X是一个终结符,且X在Follow (B) 中时,s 中没有完 整的项目B→g.。 2) 对于在s 中的任何两个完整项目A→a.和B→b.,F o l l o w (A) Follow(B)为空。 1 6 0 编译原理及实践 实际上,任何文法扩充的开始状态S¢ 的F o l l o w集合总是只由$组成,这是因为S¢ 只出现在文法规则S¢ →S中。 下载

China-pub.com 第5章自底向上的分析 161 下载 均满足时,文法为SLR(I): 若第1个条件不满足,就表示这是一个移进-归约冲突(shin-reduce conflict)。若第2个条件 不满足,就表示这是一个归约-归约冲突(reduce-reduce conflict)。 这两个条件同前一章中所述的LL()分析的两个条件在本质上是类似的。但是如同使用所 有的移进-归约分析方法一样,可将决定使用哪个文法规则推迟到最后,同时还可考虑一个更 强大的分析程序。 SLR(I)分析的分析表也可以用与前一节所述的LR(O)分析的分析表的类似方式构造。两者 的差别如下:由于状态在SL(1)分析程序中可以具有移进和归约(取决于先行),输入部分中的 每项现在必须要有一个“移进”或“归约”的标签,而且文法规则选择也必须被放在标有“归 约”的项中。这还使得动作和规则列成为多余。由于输入结束符号$也可成为一个合法的先行, 所以必须为这个符号在输入部分建立一个新的列。我们将SLR(1)分析表的构造放在SLR(1)分析 的第1个示例中。 例5.10考虑例5.8中的文法,它的项目集合的DFA已列在了图5-4中。正如前面所述的,这个 文法不是LR(O),而是SLR(I)。非终结符的Follow集合是Follow(E)={$}和Follow(E)={$,+}。 表5-5是SLR(1)分析表。在表中,移进由表项中的字母s指出,归约由字母r指出。因此,在输 入+的状态1中,指出了一个移进,以及一个到状态3的转换。另一方面,在输入+的状态2中, 指出了利用产生式E一n归约。在输入$的状态1中还用动作“接受”代替了r(E一E)。 表5-5例5.10的SLR(1)分析表 翰入 Goto n + E 接受 r(En r(E-n) E-E+) r(E-E+n) 这个示例的最后是串n+n+n的分析。表5-6是它的分析步骤。该图的步骤1以输入记号n 的状态0开始,接着分析表指出动作“s2”,即:将记号移进到栈中并进入到状态2。在表5-6中, 将它与阶段“shin2” 起指出来。在该图的步骤2中,分析程序是在状态2中且带有输入记号 +,表还指出了用规则E·n归约。此时,从栈中弹出状态2和记号n。使状态0腿盛出来。将符 号E压入且将E的Goo从状态0带到状态1。第3步中的分析程序是带有输入记号+的状态1,且表 还指出了移进以及指向状态3的转换。在输入的状态3中,表也指出了一个移进和到状态4的 转换。在输入+的状态4中,表指出用规则E一E+n归约。这个归约是由将串E+n和与它相结 合的来自栈的状态弹出来完成的,并再一次禁露状态0,将E压入并将Gto带到状态1中。分析 的其他步骤是类似的。 表5-6例5.10的分析动作 分析栈 输入 动作 n+atas 移进2
均满足时,文法为S L R ( 1 )。 若第1个条件不满足,就表示这是一个移进-归约冲突 (shift-reduce conflict)。若第2个条件 不满足,就表示这是一个归约-归约冲突(reduce-reduce conflict)。 这两个条件同前一章中所述的 L L ( 1 )分析的两个条件在本质上是类似的。但是如同使用所 有的移进-归约分析方法一样,可将决定使用哪个文法规则推迟到最后,同时还可考虑一个更 强大的分析程序。 S L R ( 1 )分析的分析表也可以用与前一节所述的 L R ( 0 )分析的分析表的类似方式构造。两者 的差别如下:由于状态在S L R ( 1 )分析程序中可以具有移进和归约 (取决于先行),输入部分中的 每项现在必须要有一个“移进”或“归约”的标签,而且文法规则选择也必须被放在标有“归 约”的项中。这还使得动作和规则列成为多余。由于输入结束符号 $也可成为一个合法的先行, 所以必须为这个符号在输入部分建立一个新的列。我们将 S L R ( 1 )分析表的构造放在S L R ( 1 )分析 的第1个示例中。 例5.10 考虑例5 . 8中的文法,它的项目集合的D FA已列在了图5 - 4中。正如前面所述的,这个 文法不是L R ( 0 ),而是S L R ( 1 )。非终结符的F o l l o w集合是F o l l o w (E¢) = {$}和Follow (E) = {$, +}。 表5 - 5是S L R ( 1 )分析表。在表中,移进由表项中的字母 s 指出,归约由字母r 指出。因此,在输 入+的状态1中,指出了一个移进,以及一个到状态 3的转换。另一方面,在输入 +的状态2中, 指出了利用产生式E→n 归约。在输入$的状态1中还用动作“接受”代替了r ( E→E )。 表5-5 例5 . 1 0的S L R ( 1 )分析表 状 态 输 入 G o t o n + $ E 0 s 2 1 1 s 3 接受 2 r (E→n) r (E→n) 3 s 4 4 r ( E→E + n) r (E→E + n) 这个示例的最后是串n + n + n 的分析。表5 - 6是它的分析步骤。该图的步骤1以输入记号n 的状态0开始,接着分析表指出动作“s 2”,即:将记号移进到栈中并进入到状态2。在表5 - 6中, 将它与阶段“shift 2”一起指出来。在该图的步骤 2中,分析程序是在状态2中且带有输入记号 +,表还指出了用规则E→n 归约。此时,从栈中弹出状态 2和记号n。使状态0曝露出来。将符 号E压入且将E的G o t o从状态0带到状态1。第3步中的分析程序是带有输入记号+的状态1,且表 还指出了移进以及指向状态 3的转换。在输入n 的状态3中,表也指出了一个移进和到状态 4的 转换。在输入+的状态4中,表指出用规则E→E + n归约。这个归约是由将串E + n和与它相结 合的来自栈的状态弹出来完成的,并再一次暴露状态 0,将E压入并将G o t o带到状态1中。分析 的其他步骤是类似的。 表5-6 例5 . 1 0的分析动作 分 析 栈 输 入 动 作 1 $ 0 n + n + n $ 移进2 第 5章 自底向上的分析 1 6 1 下载

162翁译原理及实践 China-pub.com 下载 (续) 分析栈 输入 动作 2 $0日2 +n+n$ 用E一n归约 3 SOEI +n+as 移讲3 s0E1+3 n+as 移进4 s0E1+3n4 +ns 用E+E+n归约 6 SOFI +n$ 移进3 0E1+3 移进4 8 $0E1+3n4 用E一E+n归约 9 SOEI 5 接受 例5.11考虑成对括号的文法,图5-3已给出了它的LR(O)项的DFA。一个直接的运算生成了 Follow(S)={S和Follow(S={S,)。表5-7给出了它的SLR(I)分析表。请读者注意,非LR(O) 状态0、2和4是如何通过e-产生式S一E具有移进和归约动作的。表5-8给出了SLR(1)分析算法 用来分析串()()的步骤。请注意,栈如何继续扩展到最终的归约。这是自底向上的分析程序 在诸如S一(S)S的右递归规则中的一个特征。因此,右递归可引起栈的溢出,所以若可能的 话应尽量避免。 表5-7例5.11的SLR(1)分析表 状态 输入 Goto r(S-e) r(5-e) 接受 2 52 r(S-E) r(S-E) r(S-(S)S) r(S-(s)) 表5-8例5.11的分析动作 分析钱 输入 动作 S0 ()()s 移进2 2 s0(2 )()$ 用S一e归约 34 50(2S3 移进4 0(253)4 )8 移进2 s0(2S3)4(2 )$ 用S一e归约 6 s0(2S3)4(2S3 )$ 移进4 50(253)4(253)4 用S一归约 50(253)4(2S3)4S5 用S一(S)S归约 9 50(2s3)4S5 8 用S一(S)S归约 SOSI 接受
(续) 分 析 栈 输 入 动 作 2 $ 0 n 2 + n + n $ 用E→n归约 3 $ 0 E 1 + n + n $ 移进3 4 $ 0 E 1 + 3 n + n $ 移进4 5 $ 0 E 1 + 3 n 4 + n $ 用E→E + n 归约 6 $ 0 E 1 + n $ 移进3 7 $ 0 E 1 + 3 n $ 移进4 8 $ 0 E 1 + 3 n 4 $ 用E→E + n 归约 9 $ 0 E 1 $ 接受 例5 . 11 考虑成对括号的文法,图 5 - 3已给出了它的L R ( 0 )项的D FA。一个直接的运算生成了 Follow (S¢) = {$}和Follow (S) = {$,)}。表5 - 7给出了它的S L R ( 1 )分析表。请读者注意,非L R ( 0 ) 状态0、2和4是如何通过 - 产生式S→ 具有移进和归约动作的。表 5 - 8给出了S L R ( 1 )分析算法 用来分析串( ) ( )的步骤。请注意,栈如何继续扩展到最终的归约。这是自底向上的分析程序 在诸如S→ ( S ) S的右递归规则中的一个特征。因此,右递归可引起栈的溢出,所以若可能的 话应尽量避免。 表5-7 例5 . 11的S L R ( 1 )分析表 状 态 输 入 G o t o ( ) $ S 0 s 2 r (S→ ) r (S→ ) 1 1 接受 2 s 2 r (S→ ) r (S→ ) 3 3 s 4 4 s 2 r (S→ ) r (S→ ) 5 5 r (S→ ( S ) S) r (S→ ( S ) S) 表5-8 例5 . 11的分析动作 分 析 栈 输 入 动 作 1 $ 0 ( ) ( ) $ 移进2 2 $ 0 ( 2 ) ( ) $ 用S→ 归约 3 $ 0 ( 2 S 3 ( ) $ 移进4 4 $ 0 ( 2 S 3 ) 4 ( ) $ 移进2 5 $ 0 ( 2 S 3 ) 4 ( 2 ) $ 用S→ 归约 6 $ 0 ( 2 S 3 ) 4 ( 2 S 3 ) $ 移进4 7 $ 0 ( 2 S 3 ) 4 ( 2 S 3 ) 4 $ 用S→ 归约 8 $ 0 ( 2 S 3 ) 4 ( 2 S 3 ) 4 S 5 $ 用S→ ( S ) S归约 9 $ 0 ( 2 S 3 ) 4 S 5 $ 用S→ ( S ) S归约 1 0 $ 0 S 1 $ 接受 1 6 2 编译原理及实践 下载
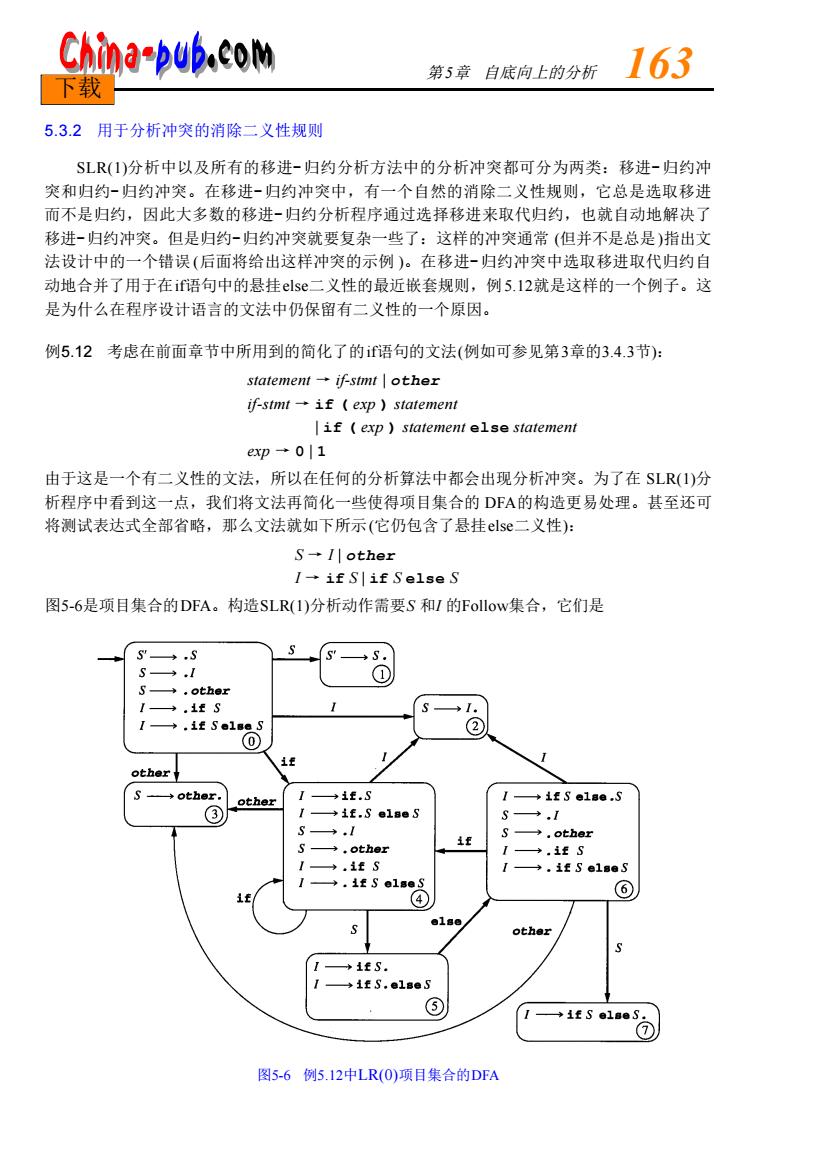
China-pub.com 第5章自底向上的分析 163 下载 5.3.2用于分析冲突的消除二义性规则 SL(1)分析中以及所有的移进-归约分析方法中的分析冲突都可分为两类:移进-归约冲 突和归约-归约冲突。在移进-归约冲突中,有一个自然的消除二义性规则,它总是选取移进 而不是归约,因此大多数的移进-归约分析程序通过选择移进来取代归约,也就自动地解决了 移进-归约冲突。但是归约-归约冲突就要复杂一些了:这样的冲突通常(但并不是总是)指出文 法设计中的一个错误(后面将给出这样冲突的示例)。在移进-归约冲突中选取移进取代归约自 动地合并了用于在if语句中的悬挂els二义性的最近嵌套规则,例5.12就是这样的一个例子。这 是为什么在程序设计语言的文法中仍保留有二义性的一个原因。 例5.12考虑在前面章节中所用到的简化了的语句的文法(例如可参见第3章的34.3节): statement-if-stmt other if-stmt→iE(ep)statement if(exp)statement else statement exD-0 1 由于这是一个有二义性的文法,所以在任何的分析算法中都会出现分析冲突。为了在SLR(I)分 析程序中看到这一点,我们将文法再简化一些使得项目集合的DFA的构造更易处理。甚至还可 将测试表达式全部省略,那么文法就如下所示(它仍包含了悬挂lse二义性): 1→if S|if Selse S 图5-6是项目集合的DFA。构造SLR(1)分析动作需要S和I的Follow集合,它们是 一 ther ot (6 ◆1S 图5-6例5.12中LR(O)项目集合的DFA
5.3.2 用于分析冲突的消除二义性规则 S L R ( 1 )分析中以及所有的移进-归约分析方法中的分析冲突都可分为两类:移进-归约冲 突和归约-归约冲突。在移进-归约冲突中,有一个自然的消除二义性规则,它总是选取移进 而不是归约,因此大多数的移进-归约分析程序通过选择移进来取代归约,也就自动地解决了 移进-归约冲突。但是归约-归约冲突就要复杂一些了:这样的冲突通常 (但并不是总是)指出文 法设计中的一个错误 (后面将给出这样冲突的示例 )。在移进-归约冲突中选取移进取代归约自 动地合并了用于在i f语句中的悬挂e l s e二义性的最近嵌套规则,例5 . 1 2就是这样的一个例子。这 是为什么在程序设计语言的文法中仍保留有二义性的一个原因。 例5.12 考虑在前面章节中所用到的简化了的i f语句的文法(例如可参见第3章的3 . 4 . 3节): statement → if-stmt | o t h e r if-stmt → i f ( exp ) s t a t e m e n t | i f ( exp ) statement e l s e s t a t e m e n t exp → 0 | 1 由于这是一个有二义性的文法,所以在任何的分析算法中都会出现分析冲突。为了在 S L R ( 1 )分 析程序中看到这一点,我们将文法再简化一些使得项目集合的 D FA的构造更易处理。甚至还可 将测试表达式全部省略,那么文法就如下所示(它仍包含了悬挂e l s e二义性): S → I | o t h e r I → i f S | i f S e l s e S 图5 - 6是项目集合的D FA。构造S L R ( 1 )分析动作需要S 和I 的F o l l o w集合,它们是 图5-6 例5 . 1 2中L R ( 0 )项目集合的D FA 第 5章 自底向上的分析 1 6 3 下载

164翁译隙理及实践 China-pub.com 下载 Follow (S)=Follow ()=is.else 现在就可以看到由悬挂else问题引起的分析冲突了。当发生在DFA的状态5中时,其中的完整项 目I→1£S.指出规则1→1£S的归约将发生在输入e1se和S中,但项目1→1£S.e1seS却指 出输入记号的一个移进将发生在e1se上。因此悬挂else将导致在SLR(1)分析表的移进-归约冲 突。很明显,用移进取代归约的消除二义性的规则可以消除这个冲突,并会根据最近嵌套规则 作出分析(若用归约取代移进,就没有办法在DFA中输入状态6或状态7,这将导致虚假的分析 错误)。 表5-9是由该文法引出的SLR(1)分析表。在该表中为归约动作中的文法规则选择使用了编 号,用它来代替写出规则本身。编号如下: (1)S→1 (2)S-other (3)1→iES (4)1-ifSelseS 请注意,无需为扩充产生式了一S端号,这是由于用该规则实现的归约与接受相对应,且在表 中已被写作“接受”了。 读者应注意到在归约项中使用的产生式编号容易引起与在移进和G0o项中所用到的编号混 淆。例如,在表5-9的表的状态5中,输入©1se下的项目是s6,它指出一个移进以及到状态6的 转换,但在输入S下的项目却是3,它指出用产生式编号3实现的归约(即:一i£S)。 表5-9还为了移进而删除了移进-归约冲突。我们将表中的项目渐渐减少以显示出在何处发 生了冲突。 表5-9例5.12的SLR(1)分析表(删除了分析冲突) 状态 输入 Goto if Else other s S1 0 4 s3 1 2 1 接受 r 3+ 2 2 2 5 3 6 s4 7 2 7 r4 r4 5.3.3SLR(1)分析能力的局限性 SLR(1)分析是LR0)分析的一个简单但有效的扩展,而LR(O)分析的能力足以处理几平所有 实际的语言结构。不幸的是,在有些情况下,SL(1)分析能力并不太强,而正由于这个原因 我们还需要学习更强大的一般的LR(1)和LALR(1)分析。下一个例子是SLR(1)分析失败的典型 情况。 例5.13考虑语句的以下文法,它是从Pascal中抽取和简化而得来的(在C中也有类似的情况
Follow (S) = Follow (I ) = {$, e l s e } 现在就可以看到由悬挂e l s e问题引起的分析冲突了。当发生在D FA的状态5中时,其中的完整项 目I → i f S.指出规则I → i f S的归约将发生在输入e l s e和$中,但项目I → i f S. e l s e S 却指 出输入记号的一个移进将发生在 e l s e上。因此悬挂e l s e将导致在S L R ( 1 )分析表的移进-归约冲 突。很明显,用移进取代归约的消除二义性的规则可以消除这个冲突,并会根据最近嵌套规则 作出分析(若用归约取代移进,就没有办法在 D FA中输入状态6或状态7,这将导致虚假的分析 错误)。 表5 - 9是由该文法引出的S L R ( 1 )分析表。在该表中为归约动作中的文法规则选择使用了编 号,用它来代替写出规则本身。编号如下: (1) S → I (2) S → o t h e r (3) I → i f S (4) I → i f S e l s e S 请注意,无需为扩充产生式 S¢→S编号,这是由于用该规则实现的归约与接受相对应,且在表 中已被写作“接受”了。 读者应注意到在归约项中使用的产生式编号容易引起与在移进和 G o t o项中所用到的编号混 淆。例如,在表5 - 9的表的状态5中,输入e l s e下的项目是s 6,它指出一个移进以及到状态 6的 转换,但在输入$下的项目却是r 3,它指出用产生式编号3实现的归约(即:I→i f S)。 表5 - 9还为了移进而删除了移进-归约冲突。我们将表中的项目渐渐减少以显示出在何处发 生了冲突。 表5-9 例5 . 1 2的S L R ( 1 )分析表(删除了分析冲突) 状 态 输 入 G o t o i f E l s e o t h e r $ S I 0 s 4 s 3 1 2 1 接受 2 r 1 r 1 3 r 2 r 2 4 s 4 s 3 5 2 5 s 6 r 3 6 s 4 s 3 7 2 7 r 4 r 4 5.3.3 SLR(1)分析能力的局限性 S L R ( 1 )分析是L R ( 0 )分析的一个简单但有效的扩展,而 L R ( 0 )分析的能力足以处理几乎所有 实际的语言结构。不幸的是,在有些情况下, S L R ( 1 )分析能力并不太强,而正由于这个原因, 我们还需要学习更强大的一般的 L R ( 1 )和L A L R ( 1 )分析。下一个例子是S L R ( 1 )分析失败的典型 情况。 例5.13 考虑语句的以下文法,它是从Pascal 中抽取和简化而得来的(在C中也有类似的情况 1 6 4 编译原理及实践 下载