
China-pub.com 第5章自底向上的分析 155 下载 NFA的初始状态应与分析程序的初始状态相对应:栈是空的,而且将要识别一个S,其中S是 文法的开始符号。因此,任何由S的产生式选择构造的初始项S一α都可作为开始状态。不幸的 是,S可能有许多这样的产生式,如何知道该选择哪一个呢?实际上,我们是无法做到这一点 的。其解决办法是通过产生式S→S扩充(augment)文法,其中S是一个新的非终结符。接着, S成为扩充文法(augmented grammar)的开始状态,且初始项S.S也成为NFA的开始状态。这 就是为什么扩充前面例子文法的原因。 在这个NFA中,哪些状态将成为接受状态呢?读者此时必须记住NFA的任务是用于了解 分析的状态,而不是如第2章中自动机那样被设计为完全识别串。因此,分析程序本身将决定 何时接受,而NFA则无需包含这一信息,所以NFA实际上根本就没有接受状态(NFA存在着有 关接受的一些信息,但并不是在接受状态中。在描述使用自动机制分析算法时还会讨论到这 一占)。 这样一来,LR(O)项的NFA的描述就完整了。现在来讨论前面两个例子的简单文法以及构 造它们的LR(O)项的NFA。 例5.55.3列出了例5.1的文法的8个LR(0)项,所以这个NFA就有8个状态,如图5-1所示。请注 意,图中在非终结符S之前带有一个句点的每个项目都有一个到S的每个初始项的ε-转换。 →5 (S)S. →(S).S 图-1例5.5中文法的LR(O)项的NFA 例5.6在例5.4中,我们列出了与例5.2中的文法相关的LR(0)项。图5-2是这些项目的NFA。请 注意,初始项E一E+·有一个到它自身的e转换(这种情况会出现在带有直接左递归的所有 文法中)。 为了完成项目用于了解分析状态的描述,我们必须根据第2章的子集构造来构建与项目的 NFA相对应的项目集合的DFA,这样之后就可说明LR(O)分析算法了。我们将执行前面刚给出 的NFA的两个例子的子集构造。 例5.7考虑图5-1的NFA。相关的DFA的开始状态是由项目S一S组成的集合的e-闭包,而这又 是3个项目的集合{S一S,S一.(S)S,S一.}由于S有一个从S一S到S一S的转换,所以也 就存在着一个从开始状态到DFA状态{S一S.}的对应转换(不存在从S一S到任何其他项目的E
N FA的初始状态应与分析程序的初始状态相对应:栈是空的,而且将要识别一个 S,其中S 是 文法的开始符号。因此,任何由 S的产生式选择构造的初始项S→.a都可作为开始状态。不幸的 是,S可能有许多这样的产生式,如何知道该选择哪一个呢?实际上,我们是无法做到这一点 的。其解决办法是通过产生式 S¢→S 扩充( a u g m e n t )文法,其中S¢是一个新的非终结符。接着, S¢ 成为扩充文法(augmented grammar)的开始状态,且初始项S¢→.S 也成为N FA的开始状态。这 就是为什么扩充前面例子文法的原因。 在这个N FA中,哪些状态将成为接受状态呢?读者此时必须记住 N FA的任务是用于了解 分析的状态,而不是如第 2章中自动机那样被设计为完全识别串。因此,分析程序本身将决定 何时接受,而N FA则无需包含这一信息,所以 N FA实际上根本就没有接受状态 ( N FA存在着有 关接受的一些信息,但并不是在接受状态中。在描述使用自动机制分析算法时还会讨论到这 一点)。 这样一来,L R ( 0 )项的N FA的描述就完整了。现在来讨论前面两个例子的简单文法以及构 造它们的L R ( 0 )项的N FA。 例5.5 5 . 3列出了例5 . 1的文法的8个L R ( 0 )项,所以这个N FA就有8个状态,如图5 - 1所示。请注 意,图中在非终结符S之前带有一个句点的每个项目都有一个到S的每个初始项的 - 转换。 图5-1 例5 . 5中文法的L R ( 0 )项的N FA 例5.6 在例5 . 4中,我们列出了与例5 . 2中的文法相关的L R ( 0 )项。图5 - 2是这些项目的N FA。请 注意,初始项E→.E + n 有一个到它自身的 - 转换(这种情况会出现在带有直接左递归的所有 文法中)。 为了完成项目用于了解分析状态的描述,我们必须根据第 2章的子集构造来构建与项目的 N FA相对应的项目集合的 D FA,这样之后就可说明 L R ( 0 )分析算法了。我们将执行前面刚给出 的N FA的两个例子的子集构造。 例5.7 考虑图5 - 1的N FA。相关的D FA的开始状态是由项目S¢→.S组成的集合的 -闭包,而这又 是3个项目的集合{ S¢→.S, S→. ( S ) S, S →. }。由于S有一个从S¢→ .S到S¢→ S.的转换,所以也 就存在着一个从开始状态到D FA状态{ S¢→ S. }的对应转换(不存在从S¢→ S.到任何其他项目的 第 5章 自底向上的分析 1 5 5 下载

156 翁译原理及实践 China-pub.Com 下载 转换)。在(上也有一个从开始状态到DFA状态的转换{S一(.S)SS.(S)S,S一.({S一( S)S;的e闭包)。DFA状态{S一(S)SS一.(S)S,S一.)在(上有到其自身的转换,在S上 也有到{S一(S)S}的转换。这个状态在(上有到状态{S(S).S,S.(S)S,S一.}的 转换。最后,这一最终状态在(上有到前面所构造的状态{S一(.S)S,S→.(S)S,S一.}的 转换。图5-3是完整的DFA,为了便于引用还给各个状态编了号(按照惯例,状态0是开始状态) E→.E E→E, E 图5-2例5.6中文法的LR(O)项的NFA ① ② S. 4 图5-3与图5的NFA相对应的项目集合的DFA 例5.8考虑图5-2的NFA。相关DFA的开始状态由3个项目的集合{E一E,E一.E+nE一n 组成。在E上有一个从项目E"一E到项目E'一E的转换,但在E上还有一个从项目E一E+n到 项目E一E.+n的转换。因此,在E上就有一个从DFA的开始状态到集合{E一E,E一E.+n} 的闭包的转换。由于没有任何一个来自这些项目的转换,所以这个集合就是它自身的闭包, 且构成了一个完整的DFA状态。来自开始状态还有另一个转换,它与符号n上的从E一.n到E →n.的转换相对应。因为没有来自项目E一n的e转换,所以这个项目是它自身的e闭包,且 构成了 个完整的DFA状态{E一n.}。由于没有来自这个状态的转换,所以被计算的唯一转 换仍来自于集合{E'一E,E一E.+n}。从该集合开始只有一个转换,它与符号+上的从项目E 一E.+n到项目E一E+,n的转换相对应。项目E一E+.n也没有e转换,所以就在DFA中构造 了一个单独的集合。最后,n上有一个从集合{E一E+.n)到集合{E→E+n}的转换。图5-4
转换)。在(上也有一个从开始状态到D FA状态的转换{ S→ (. S ) S, S→.( S ) S, S→. }({ S→ (. S ) S }的 闭包)。D FA状态{ S→ (. S ) S, S→ . ( S ) S, S→ . }在(上有到其自身的转换,在S上 也有到{ S→ ( S.) S }的转换。这个状态在(上有到状态{ S→ ( S ). S,S→ .( S ) S, S → . }的 转换。最后,这一最终状态在(上有到前面所构造的状态{ S→ (. S ) S, S→ .( S ) S, S → . }的 转换。图5 - 3是完整的D FA,为了便于引用还给各个状态编了号(按照惯例,状态0是开始状态)。 图5-2 例5 . 6中文法的L R ( 0 )项的N FA 图5-3 与图5 - 1的N FA相对应的项目集合的D FA 例5.8 考虑图5 - 2的N FA。相关D FA的开始状态由3个项目的集合{E¢→.E, E→.E + n, E →.n} 组成。在E上有一个从项目E¢→.E到项目E¢→ E.的转换,但在E上还有一个从项目E→.E + n 到 项目E→E. + n的转换。因此,在E上就有一个从D FA的开始状态到集合{ E¢→ E., E→E. + n} 的闭包的转换。由于没有任何一个来自这些项目的 转换,所以这个集合就是它自身的 闭包, 且构成了一个完整的 D FA状态。来自开始状态还有另一个转换,它与符号 n 上的从E→.n到E → n.的转换相对应。因为没有来自项目 E→n.的 转换,所以这个项目是它自身的 闭包,且 构成了一个完整的D FA状态{ E→ n. }。由于没有来自这个状态的转换,所以被计算的唯一转 换仍来自于集合{E¢→ E., E→E. + n}。从该集合开始只有一个转换,它与符号 +上的从项目E →E. + n 到项目E→E +.n 的转换相对应。项目E→E +.n 也没有 转换,所以就在D FA中构造 了一个单独的集合。最后, n 上有一个从集合{ E→E +.n}到集合{ E →E + n. }的转换。图5 - 4 1 5 6 编译原理及实践 下载
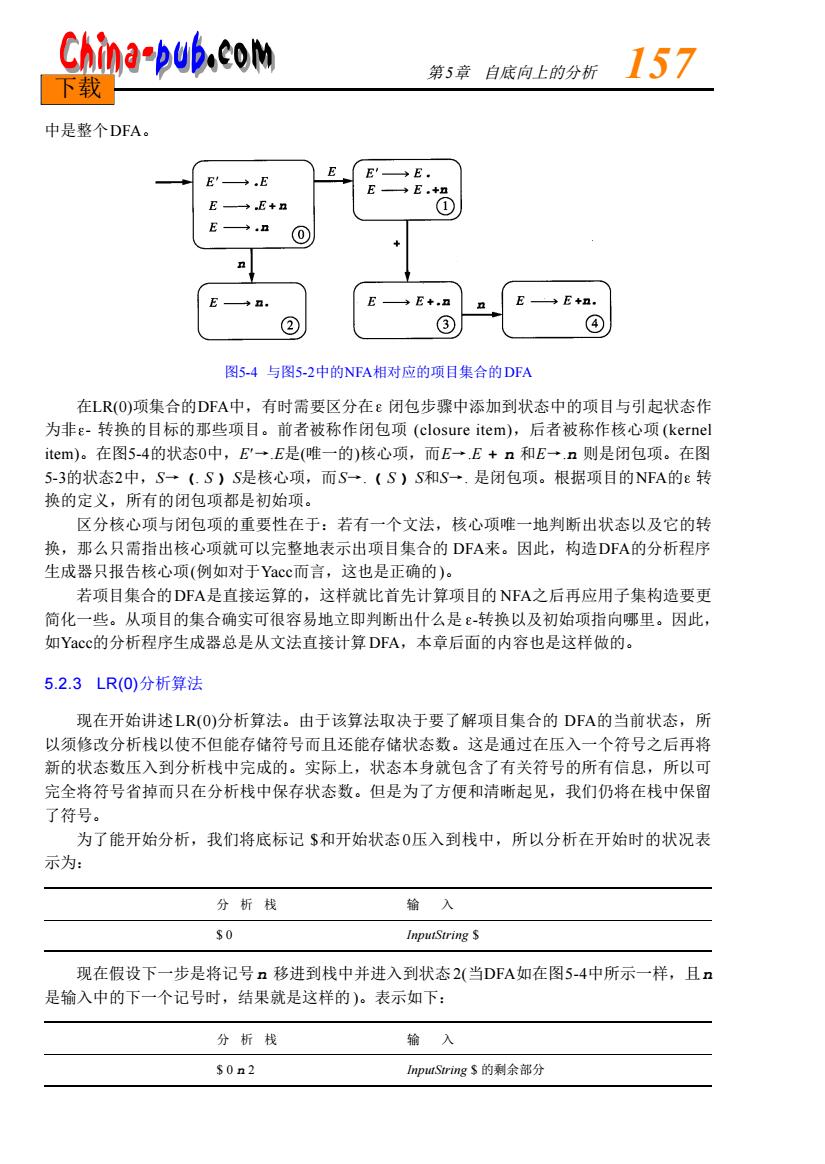
China-pub.com 第5章自底向上的分析 157 下载 中是整个DFA .E E E'→E (0 4E+,a ③ ④ 图5-4与图5-2中的NFA相对应的项目集合的DFA 在LR(O)项集合的DFA中,有时需要区分在E闭包步骤中添加到状态中的项目与引起状态作 为非e-转换的目标的那些项目。前者被称作闭包项(closure item),后者被称作核心项(kernel item)。在图5-4的状态0中,E'一E是(唯一的)核心项,而E一E+n和E,n则是闭包项。在图 53的状态2中,S一(.S)S是核心项,而S一.(S)S和S一.是闭包项。根据项目的NFA的E转 换的定义,所有的闭包项都是初始项。 区分核心项与闭包项的重要性在于:若有一个文法,核心项唯一地判断出状态以及它的转 换,那么只需指出核心项就可以完整地表示出项目集合的DFA来。因此,构造DFA的分析程序 生成器只报告核心项(例如对于Yacc而言,这也是正确的)。 若项目集合的DFA是直接运算的,这样就比首先计算项目的NFA之后再应用子集构造要更 简化一些。从项目的集合确实可很容易地立即判断出什么是-转换以及初始项指向哪里。因此, 如Yacc的分析程序生成器总是从文法直接计算DFA,本章后面的内容也是这样做的。 5.2.3LR(0)分析算法 现在开始讲述LR(O)分析算法。由于该算法取决于要了解项目集合的DFA的当前状态,所 以须修改分析栈以使不但能存储符号而且还能存储状态数。这是通过在压入一个符号之后再将 新的状态数压入到分析栈中完成的。实际上,状态本身就包含了有关符号的所有信息,所以可 完全将符号省掉而只在分析栈中保存状态数。但是为了方便和清晰起见,我们仍将在栈中保留 了符号。 为了能开始分析,我们将底标记$和开始状态0压入到栈中,所以分析在开始时的状况表 示为 分析栈 输入 InputString S 现在假设下一步是将记号n移进到栈中并进入到状态2(当DFA如在图5-4中所示一样,且n 是输入中的下一个记号时,结果就是这样的)。表示如下: 分析栈 输入 的剩余部分
中是整个D FA。 图5-4 与图5 - 2中的N FA相对应的项目集合的D FA 在L R ( 0 )项集合的D FA中,有时需要区分在 闭包步骤中添加到状态中的项目与引起状态作 为非 - 转换的目标的那些项目。前者被称作闭包项 (closure item),后者被称作核心项 ( k e r n e l i t e m )。在图5 - 4的状态0中,E¢→.E是(唯一的)核心项,而E→.E + n 和E→.n 则是闭包项。在图 5 - 3的状态2中,S→ (. S ) S是核心项,而S→. ( S ) S和S→. 是闭包项。根据项目的N FA的 转 换的定义,所有的闭包项都是初始项。 区分核心项与闭包项的重要性在于:若有一个文法,核心项唯一地判断出状态以及它的转 换,那么只需指出核心项就可以完整地表示出项目集合的 D FA来。因此,构造D FA的分析程序 生成器只报告核心项(例如对于Ya c c而言,这也是正确的)。 若项目集合的D FA是直接运算的,这样就比首先计算项目的 N FA之后再应用子集构造要更 简化一些。从项目的集合确实可很容易地立即判断出什么是 -转换以及初始项指向哪里。因此, 如Ya c c的分析程序生成器总是从文法直接计算D FA,本章后面的内容也是这样做的。 5.2.3 LR(0)分析算法 现在开始讲述L R ( 0 )分析算法。由于该算法取决于要了解项目集合的 D FA的当前状态,所 以须修改分析栈以使不但能存储符号而且还能存储状态数。这是通过在压入一个符号之后再将 新的状态数压入到分析栈中完成的。实际上,状态本身就包含了有关符号的所有信息,所以可 完全将符号省掉而只在分析栈中保存状态数。但是为了方便和清晰起见,我们仍将在栈中保留 了符号。 为了能开始分析,我们将底标记 $和开始状态0压入到栈中,所以分析在开始时的状况表 示为: 分 析 栈 输 入 $ 0 InputString $ 现在假设下一步是将记号n 移进到栈中并进入到状态2 (当D FA如在图5 - 4中所示一样,且n 是输入中的下一个记号时,结果就是这样的 )。表示如下: 分 析 栈 输 入 $ 0 n 2 InputString $ 的剩余部分 第 5章 自底向上的分析 1 5 7 下载

158 翁译原理及实践 China-pub.co 下载 LR(O)分析算法根据当前的DFA状态选择一个动作,这个状态总是出现在栈的顶部。 定义:LR(O)分析算法(LR(O)parsing algorithm)。令s为当前的状态(位于分析栈的顶 部)。则动作定义如下: 1.若状态s包含了格式A→α邓的任何项目,其中X是一个终结符,则动作就是将 当前的输入记号移进到栈中。若这个记号是X,且状态s包含了项目A一→αX郑, 则压入到栈中的新状态就是包含了项目A→αXB的状态。若由于位于刚才所描 述的格式的状态s中的某个项目,这个记号不是X,则声明一个错误。 2.若状态s包含了任何完整的项目(格式A→a.的一个项目),则动作是用规则A→α 归约。假设输入为空,用规则S一S归约(其中S是开始状态)与接受相等价:若输 入不为空,则出现错误。在所有的其他情况中,新状态的计算如下:将串α及它 的所有对应状态从分析栈中删去(根据DFA的构造方式,串α必须位于栈的顶部)。 相应地,在DFA中返回到由a开始构造的状态中(这须是由α的刷除所揭示的状 态)。由于构造DFA,这个状态就还须包含格式B一QAB的一个项目。将A压入到 栈中,并压入包含了项目B一AB的状态(作为新状态)。(请注意,由于正将 压入到栈中,所以这与在DFA中跟随A的转换相对应(这实际上是合理的)。 若以上的规则都是无歧义的,则文法就是LR(O)文法(LR(O)grammar)。这就意味着若 状态包含了完整项目A→α.,那么它就不能再包含其他项目了。实际上,若这样的状态还包含 了一个“移进的”项目A→α郑(X是一个终结符),就会出现一个到底是执行动作(1)还是执 行动作(2)的二义性。这种情况称作移进-归约冲突(shift-reduce confliet)。类似地,如果这样 的状态包含了另一个完整项目B一B.,那么也会出现一个关于为该归约使用哪个产生式(4→α 或B一B)二义性。这种情况称作归约-归约冲突(reduce-reduce conflict))。所以,当仅当每个 状态都是移进状态(仅包含了“移进”项目的状态)或包含了单个完整项目的归约时,该文法才 是LR(O). 我们注意到上面例子中所用到的两个文法都不是LR(O)文法。在图5-3中,状态0、状态2和 状态4都包括了对于LR(O)分析算法的移进-归约冲突:在图5-4的DFA中,状态1包含了一个移 进-归约冲突。由于几乎所有“真正的”文法都不是LR(O),所以这并不奇怪。但下面将会给出 一个文法是LR(O)的示例。 例5.9考虑文法 A-(A)川a 扩充的文法具有如图5-5所示的项目集合的DFA,而这就是LR(O)。为了看清LR(O)分析算法 是如何工作的,可考虑一下串(a)。该串的分析是根据表5-3各步骤所给出的LR(O)分析算 法进行。分析开始于状态0,因为这个状态是一个移进状态,所以将第1个记号(移进到栈中。 接着,由于DFA指出了在符号(上从状态0到状态3的转换,所以将状态3压入到栈中。状态3 也是一个移进状态,所以下一个(也被移进到栈中,而且在(上的转换返回到状态3。移进再 一次将a放入到栈中,而且a上的转换由状态3进入到状态2。现在位于表5-3的第4步,而且 己到达了第1个归约状态。这里的状态2和符号a都是由栈弹出的,并回到处理中的状态3。接 着,将A压入到栈中,且得到由状态3到状态4的4转换。状态4是一个移进状态,所以)被移 进到栈中,且)上的转换使分析转到状态5。这里发生了一个由规则A一(A)进行的归约 它从栈中弹出状态5、状态4、状态3以及符号)、A和)。现在的分析位于状态3中,而且A和
L R ( 0 )分析算法根据当前的D FA状态选择一个动作,这个状态总是出现在栈的顶部。 定义:L R ( 0 )分析算法(LR(0) parsing algorithm)。令s 为当前的状态(位于分析栈的顶 部)。则动作定义如下: 1. 若状态s 包含了格式A→a.Xb的任何项目,其中X是一个终结符,则动作就是将 当前的输入记号移进到栈中。若这个记号是 X,且状态s 包含了项目A→a.Xb, 则压入到栈中的新状态就是包含了项目 A→aX.b的状态。若由于位于刚才所描 述的格式的状态s 中的某个项目,这个记号不是X,则声明一个错误。 2. 若状态s 包含了任何完整的项目(格式A→a. 的一个项目),则动作是用规则A→a 归约。假设输入为空,用规则S¢→S归约(其中S是开始状态)与接受相等价;若输 入不为空,则出现错误。在所有的其他情况中,新状态的计算如下:将串a及它 的所有对应状态从分析栈中删去(根据DFA的构造方式,串a必须位于栈的顶部)。 相应地,在D FA中返回到由a开始构造的状态中(这须是由a的删除所揭示的状 态)。由于构造D FA,这个状态就还须包含格式B→a.Ab的一个项目。将A压入到 栈中,并压入包含了项目B→aA.b的状态(作为新状态)。(请注意,由于正将A 压入到栈中,所以这与在DFA中跟随A的转换相对应(这实际上是合理的)。 若以上的规则都是无歧义的,则文法就是 L R ( 0 )文法(LR(0) grammar)。这就意味着若一个 状态包含了完整项目A→a.,那么它就不能再包含其他项目了。实际上,若这样的状态还包含 了一个“移进的”项目 A→a.Xb(X是一个终结符 ),就会出现一个到底是执行动作 ( 1 )还是执 行动作( 2 )的二义性。这种情况称作移进-归约冲突 (shift-reduce conflict)。类似地,如果这样 的状态包含了另一个完整项目 B→b.,那么也会出现一个关于为该归约使用哪个产生式 (A→a 或B→b)二义性。这种情况称作归约-归约冲突 (reduce-reduce conflict)。所以,当仅当每个 状态都是移进状态(仅包含了“移进”项目的状态 )或包含了单个完整项目的归约时,该文法才 是L R ( 0 )。 我们注意到上面例子中所用到的两个文法都不是 L R ( 0 )文法。在图5 - 3中,状态0、状态2和 状态4都包括了对于L R ( 0 )分析算法的移进-归约冲突;在图 5 - 4的D FA中,状态1包含了一个移 进-归约冲突。由于几乎所有“真正的”文法都不是 L R ( 0 ),所以这并不奇怪。但下面将会给出 一个文法是L R ( 0 )的示例。 例5.9 考虑文法 A→ ( A ) | a 扩充的文法具有如图 5 - 5所示的项目集合的 D FA,而这就是 L R ( 0 )。为了看清 L R ( 0 )分析算法 是如何工作的,可考虑一下串 ( ( a ) )。该串的分析是根据表 5 - 3各步骤所给出的 L R ( 0 )分析算 法进行。分析开始于状态 0,因为这个状态是一个移进状态,所以将第 1个记号(移进到栈中。 接着,由于 D FA指出了在符号 (上从状态0到状态3的转换,所以将状态 3压入到栈中。状态 3 也是一个移进状态,所以下一个 (也被移进到栈中,而且在 (上的转换返回到状态 3。移进再 一次将a放入到栈中,而且 a上的转换由状态 3进入到状态 2。现在位于表 5 - 3的第4步,而且 已到达了第1个归约状态。这里的状态 2和符号a都是由栈弹出的,并回到处理中的状态 3。接 着,将A压入到栈中,且得到由状态 3到状态4的A转换。状态 4是一个移进状态,所以 )被移 进到栈中,且 )上的转换使分析转到状态 5。这里发生了一个由规则 A→ ( A ) 进行的归约, 它从栈中弹出状态 5、状态 4、状态3以及符号)、A和)。现在的分析位于状态 3中,而且A和 1 5 8 编译原理及实践 下载

China-pub.com 第5章自底向上的分析 159 下载 状态4又被压入到栈中。)再一次被移进到栈中,且压入状态5。由4一(A)进行的另一个 归约从栈中(向后地)别除了串(3A4)5,而将分析留在状态0中。现在A已被压入且也得到 了由状态0到状态1的4转换。状态1是接受状态。由于输入现在是空的,则分析算法承认它。 A'→,A a. ② A A一⊙ 图55例5.9的项目集合的DFA 表5-3例5.9的分析动作 分析栈 输入 动作 $0 ((a))s 移进 2 s0(3 (a))s 移进 3 $0(3(3 a))$ 移 50(3(3a 用一a归的 $0(3(3A4 )) 6 $0(3(3A4)5 )$ 用A一(A)归约 7 50《3A4 )5 移进 8 s0(3A3)5 (4)归约 9 80A1 $ 接受 也可将项目集合的DFA以及由LR(O)分析算法指定的动作合并到分析表中,所以LR(O) 分析就变成一个表驱动的分析方法了。其典型结构是:表的每行用DFA的状态标出,而每 一个列也如下标出。由于LR(O)分析状态是“移进的”状态或“归约的”状态,所以专门利 用一列来为每个状态指出它。若是“归约的”状态,就用另一个列来指出在归约中所使用 的文法规则选择。若是移进的状态,将被移进的符号会判断出下一个状态(通过DFA),所 以每个记号都会有一个列,而这些记号的各项都是有关该记号移进后将移到的新状态。由 于不能在输入中真正地看到它们,所以尽管分析程序的行为好像是它们被移进了,非终结 符上的转换(在归约时被压入)仍代表着一个特殊情况。因此,在“移进的”状态中还需要 为每个非终结符有一个列,而且按照惯例,这些列被列入到称为g0部分的表的一个单独 部分中。 表54就是这样的分析表的一个例子,它是例5.9中文法的表格。读者可以证实这个表将引 出如在表5-3中给出的示例的分析动作
状态4又被压入到栈中。 )再一次被移进到栈中,且压入状态 5。由A→ ( A ) 进行的另一个 归约从栈中(向后地)删除了串( 3 A 4 ) 5,而将分析留在状态 0中。现在A已被压入且也得到 了由状态0到状态1的A转换。状态1是接受状态。由于输入现在是空的,则分析算法承认它。 图5-5 例5 . 9的项目集合的D FA 表5-3 例5 . 9的分析动作 分 析 栈 输 入 动 作 1 $ 0 ( ( a ) ) $ 移进 2 $ 0 ( 3 ( a ) ) $ 移进 3 $ 0 ( 3 ( 3 a ) ) $ 移进 4 $ 0 ( 3 ( 3 a 2 ) ) $ 用A→ a归约 5 $ 0 ( 3 ( 3 A 4 ) )$ 移进 6 $ 0 ( 3 ( 3 A 4 ) 5 ) $ 用A→ ( A ) 归约 7 $ 0 ( 3 A 4 ) $ 移进 8 $ 0 ( 3 A 3 ) 5 $ 用A→ ( A ) 归约 9 $ 0 A 1 $ 接受 也可将项目集合的 D FA以及由L R ( 0 )分析算法指定的动作合并到分析表中,所以 L R ( 0 ) 分析就变成一个表驱动的分析方法了。其典型结构是:表的每行用 D FA的状态标出,而每 一个列也如下标出。由于 L R ( 0 )分析状态是“移进的”状态或“归约的”状态,所以专门利 用一列来为每个状态指出它。若是“归约的”状态,就用另一个列来指出在归约中所使用 的文法规则选择。若是移进的状态,将被移进的符号会判断出下一个状态 (通过D FA ),所 以每个记号都会有一个列,而这些记号的各项都是有关该记号移进后将移到的新状态。由 于不能在输入中真正地看到它们,所以尽管分析程序的行为好像是它们被移进了,非终结 符上的转换 (在归约时被压入 )仍代表着一个特殊情况。因此,在“移进的”状态中还需要 为每个非终结符有一个列,而且按照惯例,这些列被列入到称为 g o t o部分的表的一个单独 部分中。 表5 - 4就是这样的分析表的一个例子,它是例 5 . 9中文法的表格。读者可以证实这个表将引 出如在表5 - 3中给出的示例的分析动作。 第 5章 自底向上的分析 1 5 9 下载