
Certificate complexity X 。 Restricting a few variables fixes the function value. Eg.Fixing three edges make a graph to have a triangle. .C(f,x)=the minimum number of variables needed to be restricted to fix f(x). Certificate complexity of f: C(f)=max C(f,x) 2
Certificate complexity • Restricting a few variables fixes the function value. – Eg. Fixing three edges make a graph to have a triangle. • 𝐶 𝑓, 𝑥 = the minimum number of variables needed to be restricted to fix 𝑓 𝑥 . • Certificate complexity of 𝑓: 𝐶 𝑓 = max 𝑥 𝐶 𝑓, 𝑥 𝑥
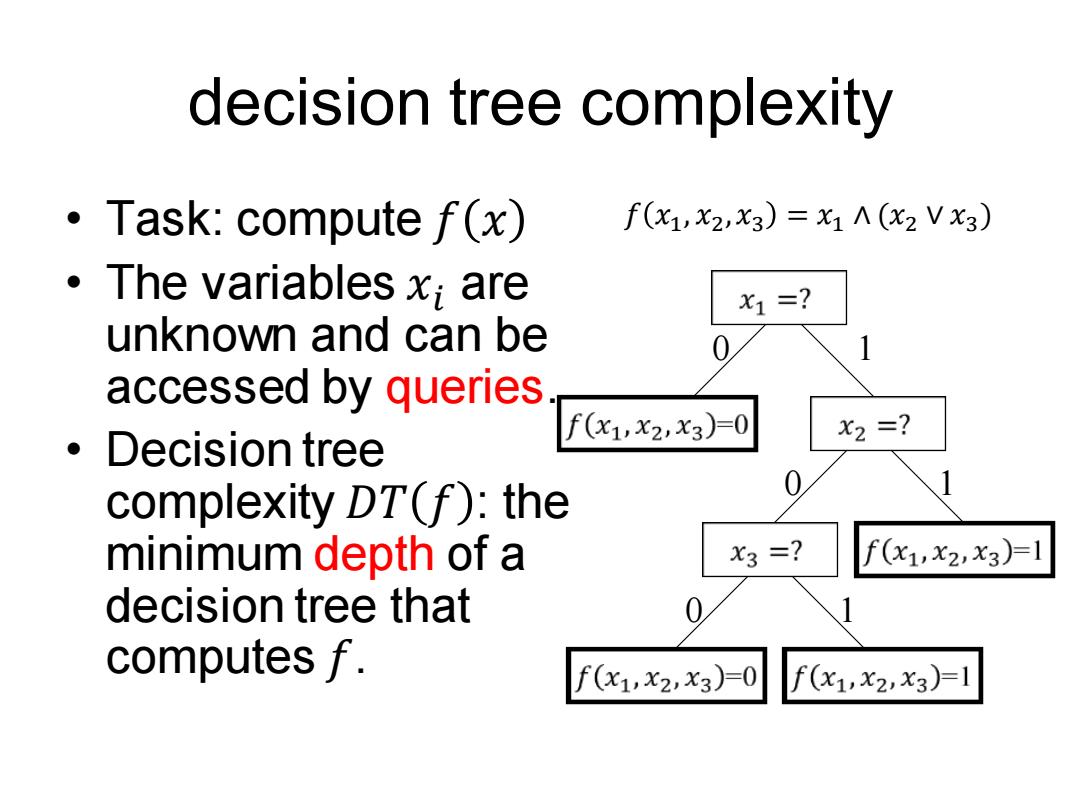
decision tree complexity ·Task:compute f(x) f(x1,x2,x3)=x1A(x2 VX3) 。The variables x;are X1=? unknown and can be 0 accessed by queries f(x1,X2,x3=0 ·Decision tree X2=? complexity DT(f):the minimum depth of a X3=? f(x1,x2,x3)=1 decision tree that computes f. f(x1,x2,x3=0 f(x1,x2,x3)1
decision tree complexity 0 1 0 1 0 1 𝑓 𝑥1 , 𝑥2 ,𝑥3 = 𝑥1 ∧ (𝑥2 ∨ 𝑥3 ) • Task: compute 𝑓 𝑥 • The variables 𝑥𝑖 are unknown and can be accessed by queries. • Decision tree complexity 𝐷𝑇 𝑓 : the minimum depth of a decision tree that computes 𝑓

Big open question 1 There are many other complexity measures. Polynomial degree,randomized/quantum DT,.. 。It turns out that for any f:{0,1n→{0,l,all these measures are polynomially related... -e.g.bs(f)≤C(f)≤DT(f)≤bs(f)3 ....except for sensitivity s(f). No example separates s(f)from the family. Sensitivity Conjecture:bs(f)=poly(s(f))
Big open question 1 • There are many other complexity measures. – Polynomial degree, randomized/quantum DT, … • It turns out that for any 𝑓: 0,1 𝑛 → 0,1 , all these measures are polynomially related… – e.g. 𝑏𝑠 𝑓 ≤ 𝐶 𝑓 ≤ 𝐷𝑇 𝑓 ≤ 𝑏𝑠 𝑓 3 • …except for sensitivity 𝑠 𝑓 . • No example separates 𝑠 𝑓 from the family. • Sensitivity Conjecture: 𝑏𝑠 𝑓 = 𝑝𝑜𝑙𝑦 𝑠 𝑓

Communication complexity F(x,y) Two parties,Alice and Bob,jointly compute a function F on input (x,y). -x known only to Alice and y only to Bob. Communication complexity*1:how many bits are needed to be exchanged? *1.A.Ya0.STOC,1979
Communication complexity • Two parties, Alice and Bob, jointly compute a function 𝐹 on input (𝑥, 𝑦). – 𝑥 known only to Alice and 𝑦 only to Bob. • Communication complexity* 1 : how many bits are needed to be exchanged? 𝐹(𝑥, 𝑦) 𝑥 𝑦 *1. A. Yao. STOC, 1979

Log-rank conjecture Not only interesting on its own,but also important because of numerous applications to prove lower bounds. 0 Question:How to lower bound communication complexity itself? y Communication matrix X→ F(x,y) ME [F(x,y)]x.y: 10
Log-rank conjecture • Not only interesting on its own, but also important because of numerous applications. – to prove lower bounds. • Question: How to lower bound communication complexity itself? • Communication matrix 𝑀𝐹 ≝ 𝐹 𝑥, 𝑦 𝑥,𝑦: 10 𝑥 → 𝑦 ↓ 𝐹(𝑥, 𝑦)