
燃烧反应的化学动力学基础一活化分子碰撞理论 1901 NG UNN ◆燃烧的反应速度 (1)净反应速度和反应级数 反应系统中某一化合物的净反应速度是该化合物在各个基元反应中的消耗 速度与生成速度的代数和。 反应级数一般由实验确定,对于基元反应,反应式中各反应物的化学计量 系数的和即为反应的级数。 确定反应级数的一种方法是通过实验测定反应物浓度大小的时间序列。 aA+bB-→cC+dD 反应速度为 -dI4l=k.LAF[B] dt 各反应物存在一定的化学计量比关系 dA]=k[A” dt School of Energy and Power Engineering
燃烧反应的化学动力学基础—活化分子碰撞理论 燃烧的反应速度 ( 1 )净反应速度和反应级数 反应系统中某一化合物的净反应速度是该化合物在各个基元反应中的消耗 速度与生成速度的代数和 。 反应级数一般由实验确定,对于基元反应,反应式中各反应物的化学计量 系数的和即为反应的级数 。 确定反应级数的 种方法是通过实验测定反应物浓度大小的时间序列 确定反应级数的 一种方法是通过实验测定反应物浓度大小的时间序列 。 aA bB cC dD + → + 反应速度为 [ ] [ ][ ] a b n d A kA B dt − = d A[ ] 各反应物存在一定的化学计量比关系 [ ] n n d A k A dt − = School of Energy and Power Engineering

燃烧反应的化学动力学基础一活化分子碰撞理论 190 等温条件下 diAl=k,dt [A]” 当反应级数=1时,反应物A的浓度随时间的变化关系 In[4]=In[4lo-kt 当反应级数>1时,反应物A的浓度随时间的变化关系 [A]-"=[A]6"+kn(n-1)i School of Energy and Power Engineering
燃烧反应的化学动力学基础 —活化分子碰撞理论 等温条件下 [ ] [ ] n n d A k dt A − = [ ] n 当反应级数 n=1时,反应物 A的浓度随时间的变化关系 0 1 ln[ ] ln[ ] A = A kt − 当反应级数 n>1时,反应物 A的浓度随时间的变化关系 1 1 0 [ ] [ ] ( 1) n n A A kn t n − − = + − School of Energy and Power Engineering
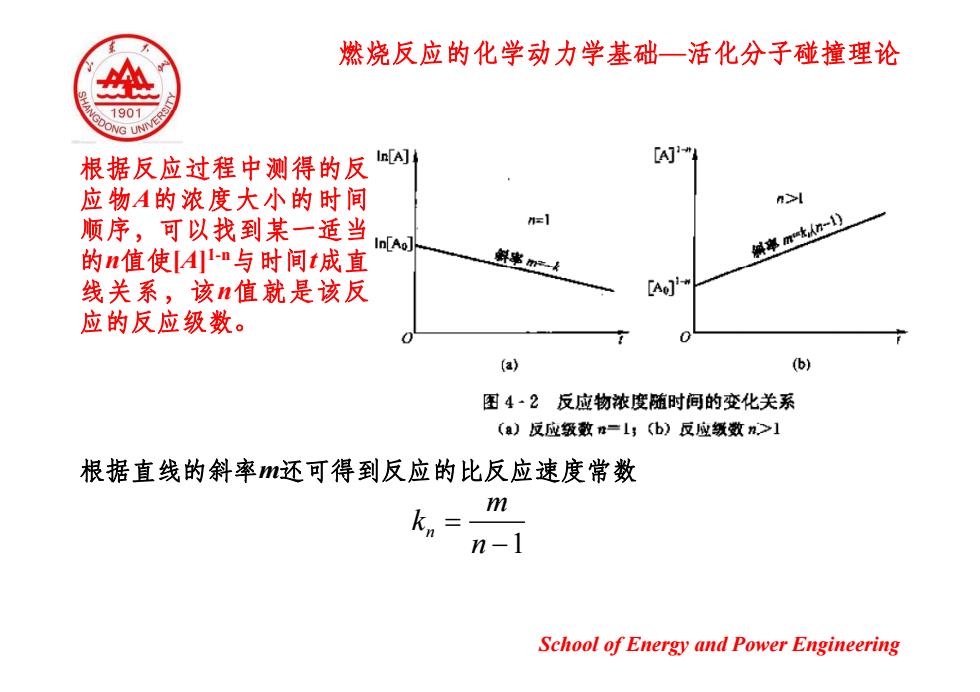
燃烧反应的化学动力学基础一活化分子碰撞理论 、1901 G UNN 根据反应过程中测得的反 In[A] 应物A的浓度大小的时间 n>l 顺序,可以找到某一适当 N=1 In[Ao] 的n值使An与时间t成直 编率mthn-) 线关系,该n值就是该反 [Ao] 应的反应级数。 (a) (b) 图4·2反应物浓度随时间的变化关系 (a)反应级数n=1;(b)反应级数n>1 根据直线的斜率还可得到反应的比反应速度常数 kn m n-1 School of Energy and Power Engineering
燃烧反应的化学动力学基础 —活化分子碰撞理论 根据反应过程中测得的反 应物 A的浓度大小的时间 顺序,可以找到某一适当 的 n值使[A] 的 n值使[A]1-n与时间 t成直 线关系,该 n值就是该反 应的反应级数。 根据直线的斜率 m还可得到反应的比反应速度常数 m 1 n k n = − School of Energy and Power Engineering

燃烧反应的化学动力学基础一活化分子碰撞理论 1901 G UNN (2)阿伦尼乌斯定律 k Aexp(- A和E是由反应特性决定的两个常数,E与反应温度及浓度无关,A徽弱的 与温度T有关; 阿伦尼鸟斯定律反映了温度对化学反应速度的影响。 School of Energy and Power Engineering
燃烧反应的化学动力学基础 —活化分子碰撞理论 ( 2)阿伦尼乌斯定律 exp( ) n E k A RT = − A 和 E是由反应特性决定的两个常数, E与反应温度及浓度无关, A微弱的 与温度 T有关; 阿伦尼乌斯定律反映了温度对化学反应速度的影响。 School of Energy and Power Engineering

燃烧反应的化学动力学基础一活化分子碰撞理论 1907 G UNN ◆反应速度的活化分子碰撞理论 装有反应物的容器中,分子杂乱无章运动能够产生化学反应的先决条件: 相配的分子必须发生碰撞;碰撞的分子中,只有一部分处于合适的方位上; 合适方位上的碰撞中只有一部分有能力足以达到化学破裂。 反应速度:WAB ZBpexp(-E/RT) (1)Maxwell--Bolt忆mann速度分布定律 存在于系统中分子总数为no,具有速度在u和u+du之间的分子数为dno dn(exp(-mi 12RT)udu no 2πRT 规定一个速度变化,对于给定气体,则可计算出各种温度下的速度分布。 School of Energy and Power Engineering
燃烧反应的化学动力学基础 —活化分子碰撞理论 反应速度的活化分子碰撞理论 装有反应物的容器中,分子杂乱无章运动能够产生化学反应的先决条件: 相配的分子必须发生碰撞;碰撞的分子中,只有一部分处于合适的方位上; 合适方位上的碰撞中只有 部分有能力足以达到化学破裂 合适方位上的碰撞中只有 一部分有能力足以达到化学破裂 。 exp( / ) 反应速度: w Z E RT AB AB ∝ − ϕ 存在 系统中分 数为 有速度在 和 的分 数为 ( 1 )Maxwell-Boltzmann速度分布定律 3/2 2 4 ( ) ( /2 ) dn m RT d 存在 于系统中分子总数为 n 0,具有速度在 u 和 u+d u之间的分 子数为 d n 。 3/2 2 0 4( ) exp( /2 ) 2 mu RT u du n RT π π = − 规定 个速度变化 规定 一个速度变化,对于给定气体,则可计算出各种温度下的速度分布 则可计算出各种温度下的速度分布 。 School of Energy and Power Engineering