
Introduction Nearest Neighbor Search(NNS)for Big Data Challenge in big data applications: o Curse of dimensionality ●Storage cost ●Query speed 日卡三4元,互Q0 Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS.NJU 6 /210
Introduction Nearest Neighbor Search (NNS) for Big Data Challenge in big data applications: Curse of dimensionality Storage cost Query speed Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 6 / 210

Introduction Similarity Preserving Hashing h(Statue of Liberty)= h(Napoleon)= h (Napoleon)= 10001010 01100001 011001Q1 flipped bit Should be very different Should be similar 0Q0 Li (http://cs.nju.edu.cn/lvj) Learning to Hash CS.NJU 7/210
Introduction Similarity Preserving Hashing Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 7 / 210
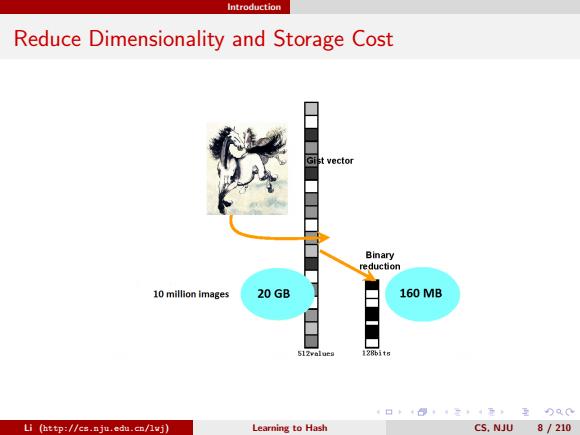
Introduction Reduce Dimensionality and Storage Cost Gist vector Binary reduction 10 million images 20 GB 160MB 口卡+得二4元互)Q0 Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS.NJU 8/210
Introduction Reduce Dimensionality and Storage Cost Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 8 / 210

Introduction Fast Query Speed o By using hash-code to construct index,we can achieve constant or sub-linear search time complexity. o In some cases,exhaustive search with linear time complexity is also acceptable because the distance calculation cost is low with binary representation. 日卡三4元,互Q0 Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS.NJU 9/210
Introduction Fast Query Speed By using hash-code to construct index, we can achieve constant or sub-linear search time complexity. In some cases, exhaustive search with linear time complexity is also acceptable because the distance calculation cost is low with binary representation. Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 9 / 210

Introduction Two Stages of Hash Function Learning Two main categories: oCategory I: Projection Stage (Dimension Reduction) Projected with real-valued projection function o Given a point x,each projected dimension i will be associated with a real-valued projection function fi(x)(e.g.,fi(x)=wx) Quantization Stage Turn real into binary o Essential difference between metric learning and learning to hash Category Il: Binary-Code Learning Stage Hash Function Learning Stage 日卡三4元,互Q0 Li (http://cs.nju.edu.cn/lvj) Learning to Hash CS.NJU 10 /210
Introduction Two Stages of Hash Function Learning Two main categories: Category I: Projection Stage (Dimension Reduction) Projected with real-valued projection function Given a point x, each projected dimension i will be associated with a real-valued projection function fi(x) (e.g., fi(x) = wT i x) Quantization Stage Turn real into binary Essential difference between metric learning and learning to hash Category II: Binary-Code Learning Stage Hash Function Learning Stage Li (http://cs.nju.edu.cn/lwj) Learning to Hash CS, NJU 10 / 210