
5,2红外光谱基本原理 never forget T how to aream 例1:由表中查知C=C键的k=9.5~9.9(N/cm),令其为9.6,计 算正己烯中C=C键伸缩振动频率,实测值为1652cm-1 9.6 =1653.2 例2:由表中查知H-Cl键的k=4.8,计算H-C键伸缩振动频, 实测值:2885.9cm-1 em)-=1370,合=1507 4.8 1.008×35.45 =2892.6 =0.98 1.008+35.45 11
例1: 由表中查知 C=C 键的 k= 9.5 ~9.9 (N/cm) ,令其为9.6, 计 算正己烯中C=C键伸缩振动频率,实测值为1652 cm-1 1653.2 2 12 9.6 (cm ) 1370 1307 -1 = = = − k v μ 例2: 由表中查知 H-Cl 键的k = 4.8 ,计算H-Cl键伸缩振动频, 实测值:2885.9cm-1 0.98 1.008 35.45 1.008 35.45 2892.6 0.98 4.8 (cm ) 1370 1307 -1 = + = = = = − k v μ μ 5.2 红外光谱基本原理 11

never forget T 5,2红外光谱基本原理 how to aream 当μ相同: C-C C=C C≡C 键力常数: 4.5-5.6 9.5-9.9 15-17 k增大 峰位: 7.0um 6.0um 4.5um 1189cm1 1667cm1 2222cm1 v增大 计算波数: 1189cm1 1684cm1 2129cm1 12
k 增大 υ 增大 当μ相同: C-C C=C C≡C 1189 cm-1 1684 cm-1 2129 cm-1 键力常数: 峰位: 4.5-5.6 9.5-9.9 15-17 4.5 μ m 2222 cm-1 7.0 μ m 1189 cm-1 6.0 μ m 1667 cm-1 计算波数: 5.2 红外光谱基本原理 12
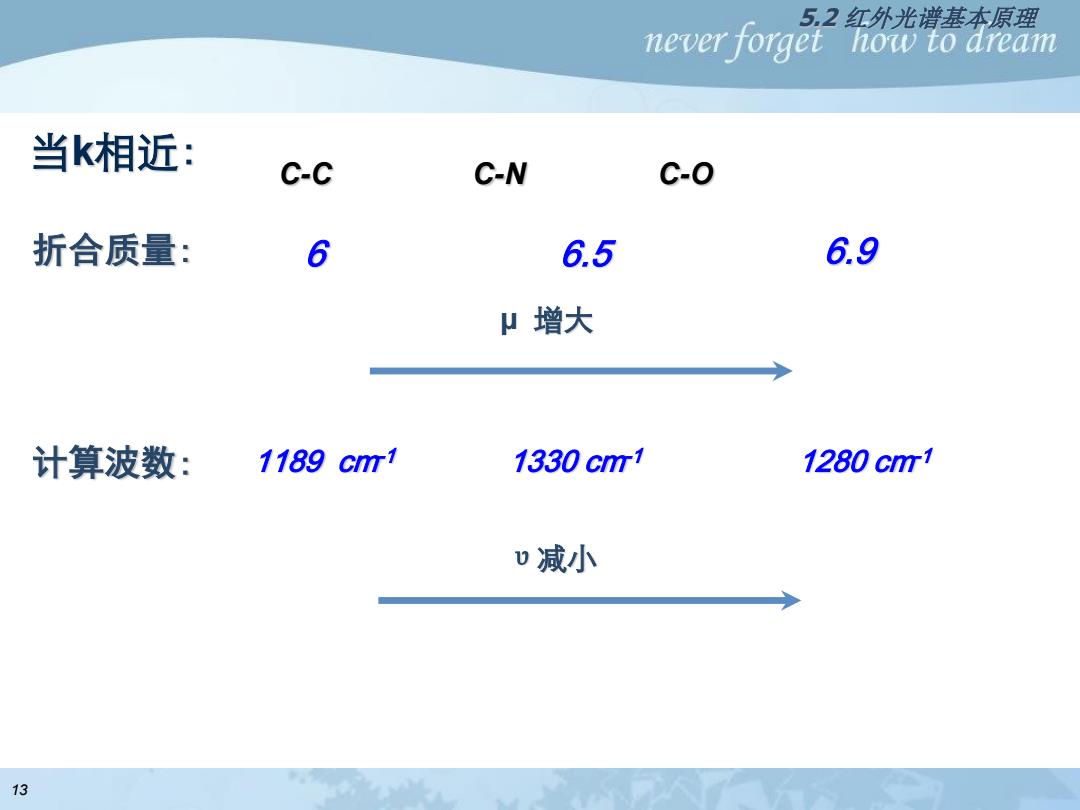
5,2红外光谱基本原理 never forget T how to aream 当k相近: c-c C-N C-O 折合质量: 6 6.5 6.9 μ增大 计算波数: 1189cm1 1330cm1 1280cm1 减小 13
μ 增大 υ减小 当k相近: 1189 cm-1 1330 cm-1 1280 cm-1 折合质量: 6 6.5 6.9 C-C C-N C-O 计算波数: 5.2 红外光谱基本原理 13
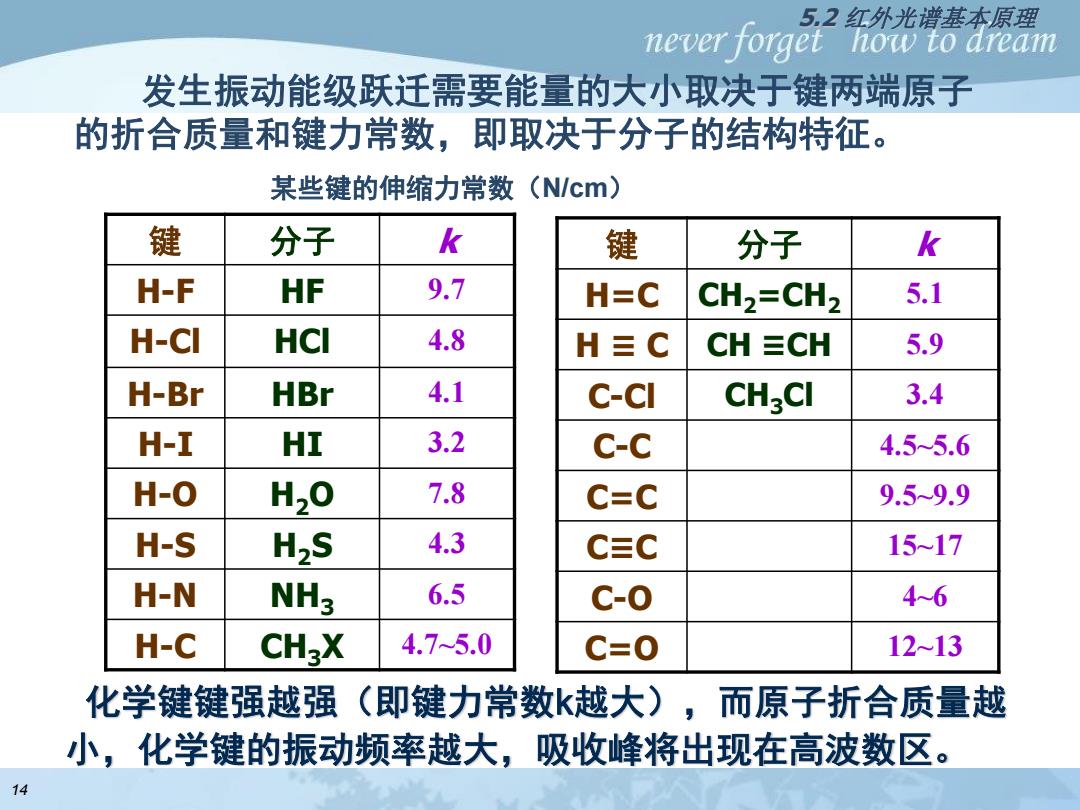
never forget T 5.2红外光谱基本原理 how to aream 发生振动能级跃迁需要能量的大小取决于键两端原子 的折合质量和键力常数,即取决于分子的结构特征。 某些键的伸缩力常数(N/cm) 键 分子 k 键 分子 k H-F HF 9.7 H=C CH,=CH2 5.1 H-CI HCI 4.8 H三C CH≡CH 5.9 H-Br HBr 4.1 C-CI CH2CI 3.4 H-I HI 3.2 C-C 4.55.6 H-O H20 7.8 C=C 9.59.9 H-S H2S 4.3 C≡C 15~17 H-N NH3 6.5 c-0 46 H-C CHX 4.75.0 C=0 12~13 化学键键强越强(即键力常数k越大), 而原子折合质量越 小,化学键的振动频率越大,吸收峰将出现在高波数区。 14
键 分子 k H=C CH2=CH2 5.1 H ≡ C CH ≡CH 5.9 C-Cl CH3Cl 3.4 C-C 4.5~5.6 C=C 9.5~9.9 C≡C 15~17 C-O 4~6 C=O 12~13 发生振动能级跃迁需要能量的大小取决于键两端原子 的折合质量和键力常数,即取决于分子的结构特征。 某些键的伸缩力常数(N/cm) 键 分子 k H-F HF 9.7 H-Cl HCl 4.8 H-Br HBr 4.1 H-I HI 3.2 H-O H2O 7.8 H-S H2S 4.3 H-N NH3 6.5 H-C CH3X 4.7~5.0 化学键键强越强(即键力常数k越大),而原子折合质量越 小,化学键的振动频率越大,吸收峰将出现在高波数区。 14 5.2 红外光谱基本原理
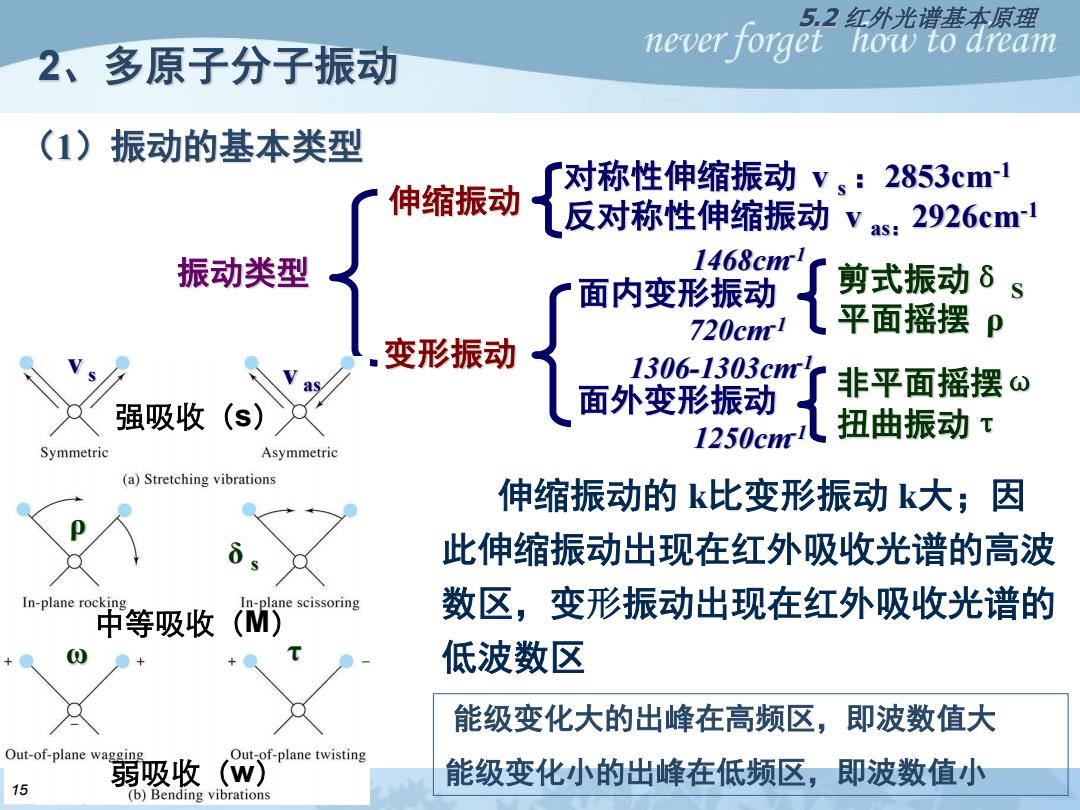
5.2红外光谱基本原理 2、多原子分子振动 never forget how to aream (1)振动的基本类型 对称性伸缩振动v、:2853cm1 伸缩振动 反对称性伸缩振动Vas: 2926cm-1 振动类型 1468cm 面内变形振动 剪式振动8s 720cm1 平面摇摆 0 变形振动 1306-1303cm1 非平面摇摆⊙ 强吸收(s) 面外变形振动 1250cmil 扭曲振动 t Symmetric Asymmetric (a)Stretching vibrations 伸缩振动的k比变形振动k大;因 此伸缩振动出现在红外吸收光谱的高波 In-plane rocking In-plane scissoring 中等吸收(M) 数区,变形振动出现在红外吸收光谱的 低波数区 能级变化大的出峰在高频区,即波数值大 Out-of-plane wagging Out-of-plane twisting 弱吸收(W) 能级变化小的出峰在低频区,即波数值小 15 (b)Bending vibrations
2、多原子分子振动 (1)振动的基本类型 对称性伸缩振动 v s :2853cm-1 反对称性伸缩振动 v as:2926cm-1 面内变形振动 面外变形振动 变形振动 振动类型 非平面摇摆ω 扭曲振动τ 剪式振动δ S 平面摇摆 ρ 伸缩振动 伸缩振动的 k比变形振动 k大;因 此伸缩振动出现在红外吸收光谱的高波 数区,变形振动出现在红外吸收光谱的 低波数区 v s v as ρ δ s ω τ 强吸收(s) 中等吸收(M) 弱吸收(w) 1468cm-1 720cm-1 1306-1303cm-1 1250cm-1 能级变化大的出峰在高频区,即波数值大 能级变化小的出峰在低频区,即波数值小 5.2 红外光谱基本原理 15